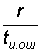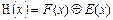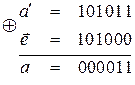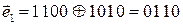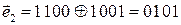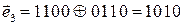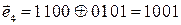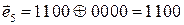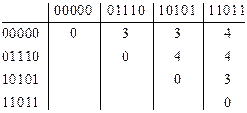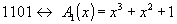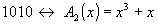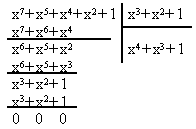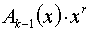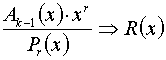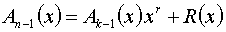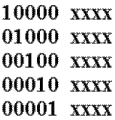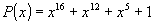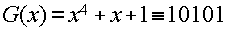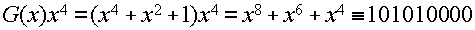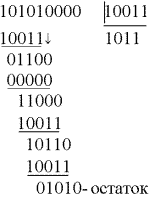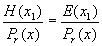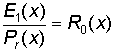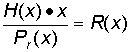определить в каком разряде принятого кодового вектора циклического кода имеется однократная ошибка
Принципы обнаружения и исправления ошибок в принятой кодовой комбинации циклического кода
Переданная кодовая комбинация двоичного циклического кода, представленная полиномом F(x), из-за искажений единичных элементов в каналах связи может быть принята с ошибками и иметь вид некоторого полинома Н(х). Если просуммировать по mod2 одноименные разряды F(х) и Н(х), то получим
F(х) 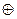
где Е(х) – полином ошибок.
Разрядность полинома ошибок такая же, как и разрядность комбинации F(х) циклического кода. При этом ненулевые разряды в Е(х) указывают на ошибочные элементы в принятой кодовой комбинации Н(х). При отсутствии ошибок полином Е(х) состоит из одних нулей.
Принимая во внимание вышеприведенные обозначения, принятую кодовую комбинацию можно представить следующим образом:
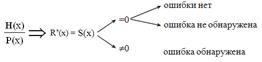
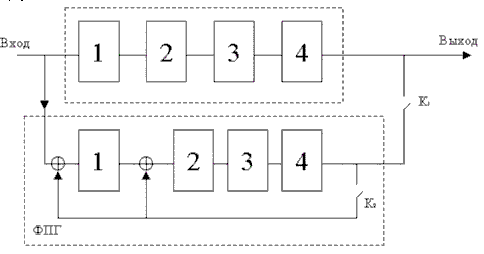
Рис.2. Схема выявления ошибок в принятой кодовой комбинации H(x)
Вид ненулевого остатка R’(x), называемого синдромом ошибки S(х), имеет однозначное соответствие с ошибочным разрядом и видом полинома однократной ошибки Е(х) для всех кодовых комбинаций Н(х) циклического кода. Например, для циклического кода (9,5) при заданном порождающем многочлене P(x)= x 4 + x + 1 остаток R’(x) всегда будет иметь вид S(х)=0011, если ошибка возникла в пятом разряде входной кодовой комбинации, т.е. в младшем информационном разряде, независимо от вида переданной кодовой комбинации F(х).
Следует отметить, что остаток R’(x), получаемый при делении полинома Н(х), на порождающий многочлен Р(х), имеет такой же вид, как и остаток от деления Е(х) на Р(х), поскольку полином F(х) делится на Р(х) без остатка.
Кратность обнаруживаемых ошибок в принятой кодовой комбинации циклического кода определяется минимальным кодовым расстоянием dmin этого кода. Для циклического кода (9,5) значение dmin=3, что обеспечивает гарантированное обнаружение всех однократных и двукратных ошибок. Кроме того, код позволяет обнаруживать часть ошибок более высокой кратности, начиная с веса, равного dmin и более. Код не обнаруживает ошибки, если полином ошибки имеет вид разрешенной кодовой комбинации.
Для исправления однократной ошибки в принятой кодовой комбинации Н(х) необходимо определить место ошибки. С этой целью также производится деление полинома Н(х) на порождающий многочлен Р(х). Для определенности вновь обратимся к коду (9,5). Если на 9 ом такта в регистре-делителе (декодирующем регистре) будет зафиксирована хотя бы одна единица, то деление продолжается до тех пор, пока в регистре-делителе не будет зафиксирована “особая” кодовая комбинация. Вид этой комбинации зависит только от вида порождающего многочлена Р(х) и длины n комбинации циклического кода F(х), причем находится “особая” кодовая комбинация как остаток от деления х n на P(x) [3]. В нашем случае, для кода (9,5) и порождающего многочлена Р(х)=х 4 +х+1 “особая” кодовая комбинация, всегда имеет вид 1010.
Номер такта, на котором в регистре-делителе возникает “особая” кодовая комбинация, указывает место ошибочного разряда в принятой кодовой комбинации Н(х). При считывании этой комбинации из буферного регистра ошибочный разряд должен быть исправлен (инвертирован).
Циклический код (9,5) гарантированно исправляет только однократные ошибки. Ошибки более высокой кратности код (9,5) не исправляет.
Заметим также, что деление полинома Н(х) на многочлен Р(х) и считывание информации из буферного регистра после 9 го такта целесообразно осуществлять под действием “быстрых” тактовых импульсов. Это позволит без задержки принять из канала связи и обработать следующую кодовую комбинацию Н(х).
1. Структурная схема кодирующего и декодирующего устройства ( циклич. Коды ).
Задачи по разделу 2
Дата добавления: 2015-08-14 ; просмотров: 3980 ; Нарушение авторских прав
Пример 1.Приняты две кодовые комбинации 0001 и 1111. Определить значность кодовых комбинаций, их вес и кодовое расстояние между комбинациями.
Решение:
1) определение значности соответствует количеству разрядов – n в кодовой комбинации: n1=n2=4.
2) определение веса по количеству «1» в комбинации: V1=1;V2=4.
3) кодовое расстояние между комбинациями – определяется как вес суммы по модулю два кодовых комбинаций: 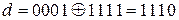
Пример 2. Принята кодовая комбинация 101011. известно, что вектор ошибки 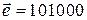
Решение:
Для нахождения кодовой комбинации определим сумму по модулю два для принятой комбинации и вектора ошибки: 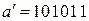
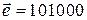
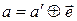
Пример 3. Передана кодовая комбинация 1100. Известно, что вес 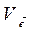
1) возможные варианты искаженных комбинаций.
2) кодовое расстояние, необходимое для обнаружения и устранения всех ошибок.
Решение:
1. Возможные варианты комбинаций состоят из тех комбинаций, которые отличаются от исходной двумя позиционными местами, т.к. 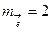
Возможные варианты:1010, 1001, 0110, 0101, 0000.
Проверим комбинации, сложив их по модулю два с исходной комбинацией: 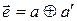
2. Для обнаружения и исправления всех ошибок необходимо, чтобы кодовое расстояние 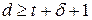
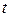
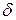
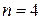
Следовательно, для их исправления и обнаружения необходимо, чтобы кодовое расстояние удовлетворило условию: 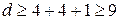
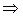
Пример 4. Определить корректирующую способность кода, имеющего следующие разрешенные комбинации: 00000, 01110, 10101, 11011.
Решение:
Построим таблицу и определим кодовые расстояния между комбинациями.
Кодовое расстояние 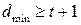
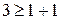
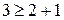
При 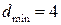
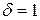
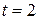
Пример 5. Определить значность кода n, обеспечивающего исправление всех однократных ошибок при количестве разрешенных комбинаций N=8.
Решение:
1) Определим значность кода по формуле: 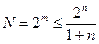
2) Определим количество информационных символов- m:

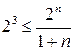
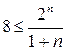
При 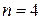
Определение места ошибки в КК циклического кода



Выбор образующего полинома
При построении циклических кодов важную роль играют образующие полиномы, поскольку они полностью определяют корректирующие свойства кода.
Непроводимыми называются такие полиномы, которые делятся без остатка только на 1 и сами на себя.
Кроме того, среди непроводимых полиномов, отбирают так называемые примитивные.
Примитивные полиномы выбираются из специальных таблиц.
В циклических кодах синдром (остаток) является опознавателем ошибки, но не указывает непосредственно на место ошибки в принятой КК.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется» под полученный остаток таким образом, что в сумме с остатком она дает исправленную комбинацию.
Остаток при этом представляет собой разницу между искаженным и исправленным разрядами. Единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами КК.
Циклически сдвигают искаженную КК до тех пор, пока число единиц в остатке не будет равно числу ошибок, которые может исправлять данный код.
При этом место ошибки не имеет значения. В этом смысле циклические коды могут исправлять пачки ошибок, если длина пачки ошибок не превышает кратность исправляемых ошибок tu
Алгоритм оптимального декодирования на основе анализа веса
1. Принятая КК делится на образующий полином
2. Если остаток нулевой, то КК выдается получателю. Если не нулевой, то выполняют п.3
4. Производим циклический сдвиг КК влево на один разряд. Делим полученную в результате сдвига КК на образующий полином. Если вес остатка w≤ tu, то складываем остаток с КК и полученную КК сдвигаем вправо на один разряд – будет исправленная КК. Если w> tu, то выполняется п.5
5. Повторяем п.4 до тех пор, пока не будет w≤ tu. КК, полученная в результате последнего циклического сдвига влево, суммируется с последним остатком. Далее выполняется п.6
6. Производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута исходная КК относительно принятой КК. В результате получим исправленную КК.
Пусть передаем КК 1001110 кода (7,4), образующий полином Р(х)=1011 (х 3 +х+1). Пусть в принятой КК искажен 4 разряд. d0=3, т.е. код исправляет однократную ошибку tu=1, т.е. приняли мы КК →1000110. Попытаемся обнаружить и исправить эту ошибку
1. Делим принятую КК на Р(х):





Получим остаток 11, его вес равен 2> tu=1
2. Производим сдвиг полученной КК влево на 1 разряд




3. Еще сдвигаем влево КК
0001101→0011010 делим на Р(х)



4. Еще сдвигаем влево КК
0011010→0110100 делим на Р(х)





5. Еще сдвигаем влево КК
0110100→1101000, делим на Р(х)









6. Складываем последнее делимое с остатком

7. Сдвинем эту КК вправо на 4 разряда, т.к. мы сдвигаем исходную КК влево на 4 разряда:
Получим исправленную КК – сравним с переданной: 1001110
Нахождение ошибок в циклическом коде
Помощь в написании контрольных, курсовых и дипломных работ здесь.
нахождение ошибок в коде, наследование
#include «stdafx.h» #include «conio.h» #include using namespace std; class.

Добрый день! Написали примитивно программу, нужно исправить, так как при нажатии на кнопку.

Добрый вечер! Я пишу простую игру (на Java). Персонаж должен убегать от гангстера. Поле это.
Нахождение ошибок
Помогите найти ошибки и переделать код (Сложение чисел) using System.Collections.Generic;.
Решение
На хабре всё неплохо разжёвано, однако, основные термины считаются сами собой разумеющимися. Типа, «Это происходит вот так, а по какой причине именно так, Вам знать не обязательно».
[7, 4] означает, что в векторе всего 7 символов, 4 из которых информационные.
Код Хэмминга может быть классическим и усечённым.
Количество символов в классическом коде Хэмминга определяется количеством проверочных символов «r». Маркировка какого-либо кода Хэмминга определяется как
Часто некоторое количество символов не используется, такие коды Хэмминга называются усечёнными.
На Хабре в примере использован усечённый код Хэмминга [21, 16], который получается из классического кода Хэмминга [31, 26] отсечением десяти символов.
На хабре не объясняется, по какому принципу определяется номер ошибочного символа: собственно, а почему «N через N начиная с N», а не как-то ещё?
Не мудрено, что Вы запутались. Тем не менее, ещё раз перечитайте хабр.
И забудьте о том, до чего Вы там досчитались. Вам по заданию нужно просто выяснить, символ с каким номером в полученном сообщении ошибочный.
Ваш вектор, проверочные символы обозначены красным цветом: 11 0 1 011.
Посимвольно, в виде таблицы:
| Имя символа | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
| Символ | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Вычислим синдромы (проверочные суммы по модулю 2):
S_1=i_1\oplus i_3\oplus i_5\oplus i_7=1\oplus 0\oplus 0\oplus 1=0\\\\S_2=i_2\oplus i_3\oplus i_6\oplus i_7=1\oplus 0\oplus 1\oplus 1=1\\\\S_4=i_4\oplus i_5\oplus i_6\oplus i_7=1\oplus 0\oplus 1\oplus 1=1\\\\
«/>
Синдромы удобнее нумеровать по степеням двойки (то есть, 1, 2, 4, 8, 16 и т.д., а не 1, 2, 3, 4 и т.д.), поскольку (если ошибка только одна) каждый из синдромов вычисляет один из двоичных разрядов номера ошибочного символа.
Для каждого синдрома суммируются те символы, у которых в двоичном представлении их номеров двоичный разряд с весом, равным номеру синдрома, установлен в 1 (это то самое «N через N начиная с N», но не в виде «закономерности», а какое оно есть на самом деле).
В синдром номер 2 попадают символы с номерами 2, 3, 6, 7, в двоичном представлении 0 1 0, 0 1 1, 1 1 0, 1 1 1. Обратите внимание, это все те, у которых 1 во втором разряде (пометил синим).
В синдром номер 4 попадают символы с номерами 4, 5, 6, 7, в двоичном представлении 1 00, 1 01, 1 10, 1 11. Обратите внимание, это все те, у которых 1 в третьем разряде (пометил синим).
Поэтому, если вектор содержит только одну ошибку, то двоичное число, составленное из синдромов, начиная со старшего (в данном случае S4S2S1=110(2)=6(10)), и будет номером ошибочного символа, поскольку распределение символов по суммам синдромов сделано по весам разрядов двоичной системы счисления. Можно (это то же самое, но в «скрытой» форме) сложить номера синдромов, в которых произошло нарушение чётности, и получить номер символа, в котором произошла ошибка: 2+4=6.
Ответ: ошибка в шестом символе, для вычисления верного сообщения нужно инвертировать шестой символ.
Определить в каком разряде принятого кодового вектора циклического кода имеется однократная ошибка
Основы передачи дискретных сообщений
Тема 5. Защита от ошибок в системах связи
От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность.
Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение.
Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов.
В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО.
5.1 Понятие о корректирующих кодах
Пусть имеется источник сообщений с объемом алфавита К.
Если 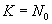
Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки.
Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия 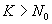
Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных.
Расстояние Хемминга – характеризует степень различия кодовых комбинаций и определяется числом несовпадающих в них разрядов.
Перебрав все возможные пары разрешенных комбинаций рассматриваемого кода можно найти минимальное расстояние Хемминга d0.
Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки.
У простого кода d0=1 – он не обнаруживает и не исправляет ошибки. Так как любая ошибка переводит одну разрешенную комбинацию в другую.
В общем случае справедливы следующие соотношения
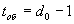
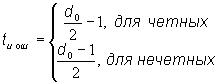
Двоичный блочный код является линейным если сумма по модулю 2 двух кодовых слов является также кодовым словом.
Линейные коды также называют групповыми.
Введем понятия группы.
Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:
Если выполняется условие gi 
Множество кодовых комбинаций n-элементного кода является замкнутой группой с заданной групповой операцией сложение по модулю 2.
Поэтому используя свойство замкнутости относительно операции 
Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.
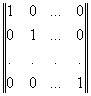
В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.
5.2 ЦИКЛИЧЕСКИЕ КОДЫ
Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов:
если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.
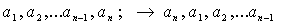
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.
Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.
Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Представление кодовой комбинации в виде многочлена.
Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов).
В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде
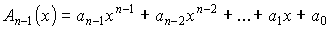
Запишем полиномы для конкретных 4-элементных комбинаций
Действия над многочленами.
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,
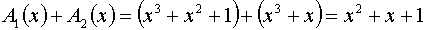
поскольку 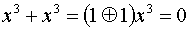
Следует отметить, что действия над коэффициентами полинома (сложение и умножение) производятся по модулю 2.
Рассмотрим операцию деления на следующем примере:
Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.
Отметим, что запись кодовой комбинации в виде многочлена, не всегда определяет длину кодовой комбинации. Например, при n = 5, многочлену 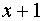
Алгоритм получения разрешенной кодовой комбинации циклического кода из комбинации простого кода
Пусть задан полином 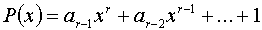
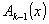
Требуется определить разрешенную кодовую комбинацию циклического кода (n, k).
Формирование базиса (производящей матрицы) циклического кода
Формирование базиса циклического кода возможно как минимум двумя путями.
Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).
В данном случае код будет неразделимым.
Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом
Построение кодера циклического кода
Рассмотрим код (9,5) образованный полиномом
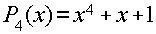
Разрешенная комбинация циклического кода 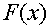
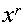
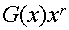
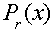
Пусть
тогда
Для реализации операции добавления нулей используется r-разрядный регистр задержки.
Как видим из примера, процедура деления одного двоичного числа на другое сводится к последовательному сложению по mod2 делителя [10011] с соответствующими членами делимого [10101], затем с двоичным числом, полученным в результате первого сложения, далее с результатом второго сложения и т.д., пока число членов результирующего двоичного числа не станет меньше числа членов делителя.
Это двоичное число и будет остатком 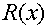
Построение формирователя остатка циклического кода
Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.
Сформулируем правила построения ФПГ.
Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.
4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.
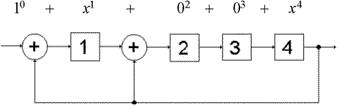
Структурная схема кодера циклического кода (9,5)
Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.
Рассмотрим работу этой схемы
1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4
2. Во время пятого такта К2 – замыкается а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.
За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток
3. К2 – размыкается, К1 – замыкается и в след за информационными в линию уйдут элементы проверочной группы.
4. Одновременно идет заполнение регистров новой комбинацией.
Второй вариант построения кодера ЦК.
Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.
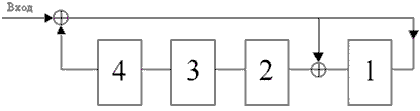
Устройство деления на производящий полином 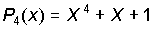
За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).
За эти же 5 тактов информационные разряды, выданные сразу на модулятор.
Далее в след за информационными уходят проверочные из ячеек устройств деления.
Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.
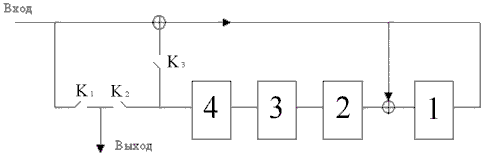
Окончательно структурная схема экономичного кодера выглядит так.
— На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.
— После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;
— на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.
Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.
Определение ошибочного разряда в ЦК.
Пусть А(х)-многочлен соответствующий переданной кодовой комбинации.
Н(х)- многочлен соответствующей принятой кодовой комбинацией.
Тогда сложение данных многочленов по модулю два даст многочлен ошибки.
E(x)=A(x) 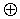
При однократной ошибке Е(х) будет содержать только один единственный член соответствующий ошибочному разряду.
Остаток – полученный от деления принятого многочлена H(x) на производящей Pr(x) равен остатку полученному при делении соответствующего многочлена ошибок E(x) на Pr(x)
При этом ошибке в каждом разряде будет соответствовать свой остаток R(x) (он же синдром), а значит, получив синдром можно однозначно определить место ошибочного разряда.
Алгоритм определения ошибки.
Пусть имеем n-элементные комбинации (n = k + r) тогда:
1. Получаем остаток от деления Е(х) соответствующего ошибке в старшем разряде [1000000000], на образующей поленом Pr(x)
2. Делим полученный полином Н(х) на Pr(x) и получаем текущий остаток R(x).
3. Сравниваем R0(x) и R(x).
— Если они равны, то ошибка произошла в старшем разряде.
— Если «нет», то увеличиваем степень принятого полинома на Х и снова проводим деления
в) Опять сравниваем полученный остаток с R0(x)
— Если они равны, то ошибки во втором разряде.
— Если нет, то умножаем Н(х)х 2 и повторяем эти операции до тех пор, пока R(X) не будет равен R0(x).
Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.
Например: 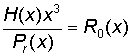
Пример декодирования комбинации ЦК.
Положим, получена комбинация H(х)=111011010
Проанализируем её в соответствии с вышеприведенным алгоритмом.
Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х 8 на производяший полином P(x)=X 4 +X+1
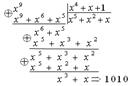
X 8 +X 5 +X 4 x 4 +x+1
Разделим принятую комбинацию на образующий полином
Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.
Декодер циклического кода с исправлением ошибки
Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ.
На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.
Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.
В нашем случае инвертируется второй разряд на 11 такте.
5.3 Выбор образующего полинома
Рассмотрим вопрос выбора образующего полинома, который определяет корректирующие свойства циклического кода. В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов mi(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома x n + 1:
Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов:
для любых значений l и tи.ош существует циклический код длины n =2 l – 1, исправляющий все ошибки кратности tи.ош и менее, и содержащий не более 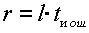
Так как 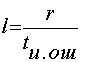
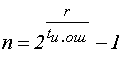
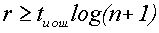
После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:
Таблица минимальных многочленов
Вид минимальных многочленов для
Определяя образующий полином, нужно из столбца для соответствующего соотношения