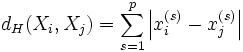формула определения расстояния хэмминга у простого кода
Расстояние Хемминга
Расстояние Хэмминга — мера (точнее, метрика) различия объектов одинаковой размерности.
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга 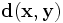
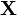
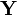
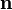
Так, расстояние Хэмминга между векторами 0 01 1 1 и 1 01 0 1 равно 2 (красным отмечены различающиеся биты). В дальнейшем метрика была обобщена на q-ичные последовательности: для пары строк « вы бор ы » и « за бор а » расстояние Хэмминга равно трём.
В общем виде расстояние Хэмминга 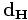
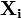
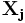
Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:
Содержание
Расстояние Хэмминга в биоинформатике и геномике
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.
Родственные методы
Литература
Ссылки
Полезное
Смотреть что такое «Расстояние Хемминга» в других словарях:
расстояние Хемминга — хемминговское расстояние Расстояние d (u,v) между двумя кодовыми последовательноаями u и v одинаковой длины, равное числу символов, в которых они отличаются. Блочный код с минимальным хемминговским расстоянием d позволяет обнаружить (d 1) и… … Справочник технического переводчика
кодовое расстояние — Минимум расстояния Хемминга, взятый по всем ларам различных кодовых слов в равномерном коде. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория… … Справочник технического переводчика
Линейный код — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Порождающая матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Проверочная матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Обнаружение и исправление ошибок — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления… … Википедия
Избыточное кодирование — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Избыточность данных — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Исправляющие ошибки Коды — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Коды, исправляющие ошибки — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Расстояние Хэмминга
Расстояние Хэмминга используется для обнаружения и исправления ошибок путем сравнения единиц данных, полученных по каналу передачи, с действительными символами. Любая коррекция персонажей основана на принципе вероятности. Возможность обнаружения или исправления ошибок зависит от расстояния Хэмминга.
Содержание
определение
Следует отметить, что расстояние Хэмминга также является метрикой в кодовом пространстве.
Примеры
| 001 1 0 и 001 0 0 | → расстояние Хэмминга = 1 |
| 1 2 34 5 и 1 3 34 4 | → расстояние Хэмминга = 2 |
| Н ая с и B Au м | → расстояние Хэмминга = 2 |
Вес Хэмминга
Расстояние Хэмминга кода
Наименьшее из трех расстояний равно 1, поэтому расстояние Хэмминга кода также равно 1.
Расстояние Хэмминга важно, если вы хотите разработать коды, которые позволяют обнаруживать ошибки ( EDC ) или исправлять ( ECC ).
Нахождение расстояния Хэмминга кода
| 4-й | 3 | 2 | 3 | 4-й |
|---|---|---|---|---|
| 3 | 2 | 1 | 2 | 3 |
| 2 | 1 | Икс | 1 | 2 |
| 3 | 2 | 1 | 2 | 3 |
| 4-й | 3 | 2 | 3 | 4-й |
Пример применения
При передаче данных необходимо убедиться, что информация не фальсифицирована или что изменения в данных, по крайней мере, заметны (обнаружение n-кратных ошибок) и, возможно, могут быть исправлены.
В следующем примере поворотный переключатель имеет четыре варианта настройки. Они передаются получателю в электронном виде в виде двоичного числа (кодового слова): 00, 01, 10, 11; Приемник получает кодовое слово, но не имеет других средств проверки или распознавания положения переключателя. В технических приложениях это уже тот случай, когда приемник представляет собой микроконтроллер, а передатчик состоит из датчиков внутри переключателя.
В этом сценарии приемник не имеет возможности распознать нарушение передачи или дефект в переключателе (например, неисправные датчики в переключателе). С помощью расстояния Хэмминга и соответствующих кодов можно найти способ обнаружения ошибок в передатчике или в линии.
Расстояние Хэмминга между четырьмя упомянутыми значениями 00, 01, 10, 11 в каждом случае равно 1, т.е. ЧАС. если из-за ошибки инвертируется только один бит, приемник получит другое, но одинаково действительное кодовое слово. Если от 00 до 01 фальсифицировано, получатель не может распознать ошибку только по сообщению, потому что и предполагаемое, и фальсифицированное значение описывают допустимое положение переключателя.
В случае единственного ошибочного бита (одиночной ошибки) ни одно из этих четырех кодовых слов 001, 010, 100, 111 не меняется на одно из трех других действительных кодовых слов. Получатель распознает, когда z. Б. Приходит 011, что, должно быть, произошла ошибка. Код с расстоянием Хэмминга 2 не может быть исправлен надежно, как показывает этот пример: 011 мог быть создан путем реверсирования всего одного бита одного из трех допустимых кодовых слов 001, 010, 111.
Если получатель предполагает, что возникают только единичные ошибки, и получатель хочет их исправить, он должен согласиться с кодовыми словами отправителя, каждое из которых имеет расстояние Хэмминга ≥ 3, например Например, 01011, 01100, 10010, 10101.
Двойная ошибка открывает возможность ошибки, как может быть показано в примере 01111: если 01111 должен был возникнуть из-за двойной ошибки из 01100, но получатель считает это одиночной ошибкой и исправляет ее, тогда 01100, фактически предназначенный отправителем, становится 01100 из-за двойной ошибки 01111 и неправильно 01011 из-за исправления получателя (из-за допущения единственной ошибки).
Из-за уже упомянутого уменьшения вероятности множественных ошибок (n-кратных ошибок) с увеличением n для большинства приложений достаточно расстояния Хэмминга от 4 (обнаружение тройных ошибок) до 5 (исправление двойных ошибок).
Требуемая длина кодового слова зависит от требуемого расстояния Хэмминга и количества возможных положений переключателя и показана в таблице выше. Здесь вы можете увидеть, например, что по крайней мере 8 битов должны быть переданы для 20 различных положений переключателя, если все 20 кодовых слов должны достичь по крайней мере расстояния Хэмминга ≥ 3 друг от друга.
Представление битовой строки в гиперкубе
пример
Если выбран код со словами <000, 101, 110, 011>, минимальное расстояние Хэмминга равно 2. При расстоянии Хэмминга 2 1-битные ошибки могут быть только распознаны, но не исправлены (например, признать, что 111 представляет собой неправильное слово, но не следует ли его исправлять после 110, 011 или 101).
Минимальное расстояние
пример
Вывод
Подсчет расстояния Хэмминга на большом наборе данных
Введение
Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.
Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.
Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.
Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.
Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.
Описание проблемы
Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.
Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.
В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.
— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.
В статье описывается решение только статической задачи.
Описание алгоритма HEngine для статической задачи
Данная реализация фокусируется на поиске строк в пределах k = ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) = ⌊k/2⌋ + 1
Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.
Теперь тоже самое, только на примере:
Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.
Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1
Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.
И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.
Предварительная обработка базы данных
Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).
Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.
Но как производить поиск по подстрокам?
Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).
В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:
Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2
Затем эти таблицы сигнатур сортируются.
Реализация поиска
На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.
Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.
Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).
Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.
А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.
Такие действия надо произвести для всех подстрок и для всех таблиц.
И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111
Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111
На этом предварительная обработка закончена. И приступаем к поиску.
1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.
2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.
2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010
2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101
3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Найдено две подстроки.
3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.
1100
0100
1000
1110 == 1110 => 00111110
1101
Найдена одна подстрока.
4. Объедением результаты в один список:
00111110
11111111
5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию
Помехоустойчивое кодирование. Коды Хэмминга
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
По используемому алфавиту:
Блочные коды делятся на
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.