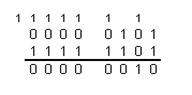
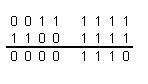
запишите обратный код числа 0112
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Запишите обратный код числа 0112
4.4. Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
[ Ответ ]
4.8. Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.
4.9. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:
| а) 10110112; | е) 5178; | л) 1F16; |
| б) 101101112; | ж) 10108; | м) ABC16; |
| в) 0111000012; | з) 12348; | н) 101016; |
| г) 0,10001102; | и) 0,348; | о) 0,А416; |
| д) 110100,112; | к) 123,418; | п) 1DE,C816. |
4.10. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
4.11. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
| а) 1001111110111,01112; | г) 1011110011100,112; |
| б) 1110101011,10111012; | д) 10111,11111011112; |
| в) 10111001,1011001112; | е) 1100010101,110012. |
4.12. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:
4.14. Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:
4.15. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]
4.16. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]
4.18. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:
4.19. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):

4.20. Вычтите:
| а) 1112 из 101002; | д) 158 из 208; | и) 1А16 из 3116; |
| б) 10,112 из 100,12; | е) 478 из 1028; | к) F9E16 из 2А3016; |
| в) 111,12 из 100102; | ж) 56,78 из 1018; | л) D,116 из B,9216; |
| г) 100012 из 1110,112; | з) 16,548 из 30,018; | м) ABC16 из 567816. |
4.21. Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения:
| а) 1011012 и 1012; | д) 378 и 48; |
| б) 1111012 и 11,012; | е) 168 и 78; |
| в) 1011,112 и 101,12; | ж) 7,58 и 1,68; |
| г) 1012 и 1111,0012; | з) 6,258 и 7,128. |
4.22. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
[ Ответ ]
4.23. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
[ Ответ ]
4.27. Запишите числа в прямом коде (формат 1 байт):
4.28. Запишите числа в обратном и дополнительном кодах (формат 1 байт):
4.29. Найдите десятичные представления чисел, записанных в дополнительном коде:
а) 1 1111000; б) 1 0011011; в) 1 1101001; г) 1 0000000.
[ Ответ ]
4.30. Найдите десятичные представления чисел, записанных в обратном коде:
а) 1 1101000; б) 1 0011111; в) 1 0101011; г) 1 0000000.
[ Ответ ]
Прямой, обратный и дополнительный двоичные коды



В компьютерной арифметике, которая базируется на двоичной системе счисления, операция «вычитания» заменяется операцией «сложения».
Рассмотрим, как это происходит.
Для хранения целых чисел в памяти ЭВМ выделяется фиксированное число двоичных разрядов – бит. Рассмотрим 8–и битовое представление числа. Каждый бит нумеруется «слева – направо» от 0 до 7.
| вес разряда нумерация бит в байте |
| 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 |  2 0 2 0 |
Старший бит – седьмой – используется для знака числа: 0 – это положительное число, 1 – отрицательное.
Если в разрядах байта с 0 по 6 поместить абсолютное значение числа, а в 7-ом бите установить его знак (0 или 1), то полученное представление числа называется прямым двоичным кодом.
Если в прямом коде число представлено как отрицательное (7-ой бит равен 1), то в числе инвертируются [1] все разряды, кроме знакового. Такое представление числа называется обратный двоичный код.
После прибавления к обратному коду 1 получается дополнительный двоичный код.
Использование дополнительного двоичного кода позволяет создавать схемы, выполняющие вычитание, умножение и деление посредством операции сложения.
Рассмотрим на примерах операцию вычитания для 8-и битовых чисел.
ПРИМЕР 1: Вычесть число 3 из 5 (1012 – 0112).
· Инвертируем все разряды в числе, кроме знакового
· Прибавим к обратному коду единицу
Проверка: Сделаем проверку, преобразуя двоичные числа к десятичному виду:
ПРИМЕР 2: Вычесть число 49 из 63
Получили число 11102 = 1410
Ответ: 11 11112 – 11 00012 = 11102
Проверка: 6310 – 4910 = 1410
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Используя схемы примера 1 или 2, сделайте вычитание целых чисел, используя дополнительный двоичный код.
| Номер варианта | Числа | Номер варианта | Числа |
| 81 и 17 | 64 и 32 | ||
| 42 и 18 | 51 и 28 | ||
| 42 и 36 | 92 и 48 | ||
| 61 и 28 | 67 и 29 | ||
| 74 и 28 | 82 и 29 | ||
| 62 и 39 | 53 и 29 | ||
| 43 и 28 | 83 и 38 | ||
| 78 и 49 | 68 и 29 |
Контрольные вопросы
1. Что такое система счисления?
2. Какие существуют системы счисления?
3. Какие непозиционные системы счисления вы знаете?
4. Приведите примеры записи чисел 467, 89011 в непозиционной системе счисления.
5. Сформулируйте правило, как определяется величина числа в римской системе счисления?
6. Для чего используются непозиционные системы счисления?
7. Чем отличаются позиционные и непозиционные системы счисления?
8. Что такое основание позиционной системы счисления?
9. Для чего используются позиционные системы счисления?
10. Может ли число 5 являться основанием системы счисления?
11. Существует ли двенадцатеричная система счисления?
12. Как математически записать любое число А в произвольной позиционной системе счисления?
13. Что является весом разряда?
14. Приведите пример, указав номер разряда и его вес.
15. Сформулируйте правило, как образуются целые числа в позиционных системах счисления?
16. Приведите пример образования трех целых чисел в шестеричной позиционной системе счисления после числа 6.
17. Что означает понятие продвижение цифры в позиционной системе счисления?
18. Как представляется десятичное число 8 в 16-ной, 8-ной и 2-ной системах счисления?
19. Какие существуют достоинства и недостатки двоичной системы счисления?
20. Что такое мощность алфавита?
21. Правило перевода целого положительного числа из 10-ной системы счисления в любую другую позиционную систему.
22. Как выглядит число 36710 в 16-ной, 8-ной и 2-ной системах счисления?
23. Правило перевода правильной десятичной дроби в любую другую позиционную систему.
24. Сделайте перевод десятичной дроби 0,75 в 16-ную, 8-ную и 2-ную системы счисления.
25. Переведите число 365,2510 в 16-ную, 8-ную и 2-ную системы счисления.
26. Правило перевода восьмеричных и шестнадцатеричных чисел в двоичную систему счисления.
27. Переведите число 1578 и C1216 в двоичную систему счисления.
28. Правило перевода числа из двоичной системы счисления в восьмеричную или шестнадцатеричную.
29. Переведите число 101000011111,110012 в восьмеричную и шестнадцатеричную системы счисления.
30. Применяя правило счета, составьте фрагмент таблицы сложения в восьмеричной и шестнадцатеричной системах счисления.
31. Сложите числа 17, 6 и 5 в различных позиционных системах счисления. Сделайте проверку.
32. Сложите числа 79,25 и 51,125 в различных позиционных системах счисления. Сделайте проверку.
33. Найдите разность чисел 99,05 и 51,25 в различных позиционных системах счисления. Сделайте проверку.
34. Какое представление числа называется прямым двоичным кодом? Приведите пример.
35. Какое представление числа называется обратным двоичным кодом? Приведите пример.
36. Что такое дополнительный двоичный код? Приведите пример.
37. Сделайте вычитание чисел 51 и 28, используя дополнительный код.
Литература
1. Андреева Е.В., Фалина И. Н. Системы счисления и компьютерная арифметика, Издательство: Лаборатория Базовых Знаний
2. Андреева Е.В. Системы счисления и компьютерная арифметика. Издание 3 Бином. Лаборатория знаний
3. Ашарина и. В. Основы программирования на языках С и С++
4. Гашков С. Б. Системы счисления и их применение
5. Гашков С. Б. Системы счисления и их применение
6. Еремина Е.А. Как работает современный компьютер