зачем программисту теория вероятностей
Вероятностное программирование
Вступление
Эта публикация является первой частью краткого вступления с иллюстрациями в вероятностное программирование, которое является одним из современных прикладных направлений машинного обучения и искусственного интеллекта. Во время написания этой публикации я с радостью обнаружил, что на Хабрахабре совсем недавно уже была статья о вероятностном программировании с рассмотрением прикладных примеров из области теории познания, хотя, к сожалению, в русскоговоряющем Интернете пока мало материалов на эту тему.
Я, автор, Юра Перов, занимаюсь вероятностным программированием в течение уже двух лет в рамках своей основной учебно-научной деятельности. Продуктивное знакомство с вероятностным программированием у меня сложилось, когда будучи студентом Института математики и фундаментальной информатики Сибирского федерального университета, я проходил стажировку в Лаборатории компьютерных наук и искусственного интеллекта в Массачусетском технологическом институте под руководством профессора Джошуа Тененбаума и доктора Викаша Мансингхи, а затем продолжилось на Факультете технических наук Оксфордского университета, где на данный момент я являюсь студентом-магистром под руководством профессора Френка Вуда.
Вероятностное программирование я люблю определять как компактный, композиционный способ представления порождающих вероятностных моделей и проведения статистического вывода в них с учетом данных с помощью обобщенных алгоритмов. Хотя вероятностное программирование не вносит много фундаментального нового в теорию машинного обучения, этот подход привлекает своей простотой: «вероятностные порождающие модели в массы!»
«Обычное» программирование
Для знакомства с вероятностным программирование давайте сначала поговорим об «обычном» программировании. В «обычном» программировании основой является алгоритм, обычно детерминированный, который позволяет нам из входных данных получить выходные по четко установленным правилам.
Например, если у нас есть мальчик Вася, и мы знаем где он находится, куда он бросает мяч и каковы внешние условия (например, сила ветра), мы узнаем, какое окно он, к сожалению, разобьет в здании школы. Для этого достаточно симулировать простые законы школьной физики, которые легко можно записать в виде алгоритма.
А теперь вероятностное программирование
Однако часто мы знаем только результат, исход, и мы заинтересованы в том, чтобы узнать то, какие неизвестные значения привели именно к этому результату? Чтобы ответить на этот вопрос с помощью теории математического моделирования создается вероятностная модель, часть параметров которой не определены точно.
Например, в случае с мальчиком Васей, зная то, какое окно он разбил, и имея априорные знания о том, около какого окна он и его друзья обычно играют в футбол, и зная прогноз погоды на этот день, мы хотим узнать апостериорные распределение местоположения мальчика Васи: откуда же он бросал мяч?
Итак, зная выходные данные, мы заинтересованы в том, чтобы узнать наиболее вероятные значения скрытых, неизвестных параметров.
В рамках машинного обучения рассматриваются в том числе порождающие вероятностные модели. В рамках порождающих вероятностных моделей модель описывается как алгоритм, но вместо точных однозначных значений скрытых параметров и некоторых входных параметров мы используем вероятностные распределениях на них.
Существует более 15 языков вероятностного программирования, перечень с кратким описанием каждого из них можно найти здесь. В данной публикации приведен пример кода на вероятностных языках Venture/Anglican, который имеют очень схожий синтаксис и которые берут свое начало от вероятностного языка Church. Church в свою очередь основан на языке «обычного» программирования Lisp и Scheme. Заинтересованному читателю крайне рекомендуется ознакомиться с книгой «Структура и интерпретация компьютерных программ», являющейся одним из лучших способов начать знакомство с языком «обычного» программирования Scheme.
Пример Байесовской линейной регрессии
Рассмотрим задание простой вероятностной модели Байесовской линейной регрессии на языке вероятностного программирования Venture/Anglican в виде вероятностной программы:
Скрытые искомые параметры — значения коэффициентов t1 и t2 линейной функции x = t1 + t2 * time. У нас есть априорные предположения о данных коэффициентах, а именно мы предполагаем, что они распределены по закону нормального распределения Normal(0, 1) со средним 0 и стандартным отклонением 1. Таким образом, мы определили в первых двух строках вероятностной программы априорную вероятность на скрытые переменные, P(T). Инструкцию [ASSUME name expression] можно рассматривать как определение случайной величины с именем name, принимающей значение вычисляемого выражение (программного кода) expression, которое содержит в себе неопределенность.
Вероятностные языки программирования (имеются в виду конкретно Church, Venture, Anglican), как и Lisp/Scheme, являются функциональными языками программирования, и используют польскую нотацию при записи выражений для вычисления. Это означает, что в выражении вызова функции сначала располагается оператор, а уже только потом аргументы: (+ 1 2), и вызов функции обрамляется круглыми скобками. На других языках программирования, таких как C++ или Python, это будет эквивалентно коду 1 + 2.
На строках 5—7 мы непосредственно вводим известные значения x1 = 10.3, x2 = 11.1, x3 = 11.9. Инструкция вида [OBSERVE expression value] фиксирует наблюдение о том, что случайная величина, принимающая значение согласно выполнению выражения expression, приняла значение value.
Отметим, что в завершении мы можем также предсказать значение функции x(time) в другой точке, например, при time = 4.0. Под предсказанием в данном случае понимается генерация выборки из апостериорного распределения новой случайной величины при значениях скрытых случайных величин t1, t2 и параметре time = 4.0.
Для генерации выборки из апостериорного распределения P(T | X) в языке программирования Venture в качестве основного используется алгоритм Метрополиса-Гастингса, который относится к методам Монте-Карло по схеме Марковских цепей. Под обобщенным выводом в данном случае понимается то, что алгоритм может быть применен к любым вероятностным программам, написанным на данном вероятностном языке программирования.
В видео, прикрепленном ниже, можно посмотреть на происходящий статистический вывод в данной модели.
(На видео показан пример, основанный на языке вероятностного программирования Venture.)
В самом начале у нас нет данных, поэтому мы видим априорное распределение прямых. Добавляя точку за точкой (таким образом, элементы данных), мы видим элементы выборки из апостериорного распределения.
На этом мы закончим первую часть данного вступления в вероятностное программирование.
Математика для программистов: теория вероятностей
Авторизуйтесь
Математика для программистов: теория вероятностей
Некоторые программисты после работы в области разработки обычных коммерческих приложений задумываются о том, чтобы освоить машинное обучение и стать аналитиком данных. Часто они не понимают, почему те или иные методы работают, и большинство методов машинного обучения кажутся магией. На самом деле, машинное обучение базируется на математической статистике, а та, в свою очередь, основана на теории вероятностей. Поэтому в этой статье мы уделим внимание базовым понятиям теории вероятностей: затронем определения вероятности, распределения и разберем несколько простых примеров.
Возможно, вам известно, что теория вероятностей условно делится на 2 части. Дискретная теория вероятностей изучает явления, которые можно описать распределением с конечным (или счетным) количеством возможных вариантов поведения (бросания игральных костей, монеток). Непрерывная теория вероятностей изучает явления, распределенные на каком-то плотном множестве, например на отрезке или в круге.
Пространство элементарных исходов
Допустим, из некоторого случайного эксперимента, который мы можем многократно повторять (например, бросание монеты), мы можем извлечь некоторую формализуемую информацию (выпал орел или решка). Эта информация называется элементарным исходом, при этом целесообразно рассматривать множество всех элементарных исходов, часто обозначаемое буквой Ω (Омега).
Структура этого пространства целиком зависит от природы эксперимента. Например, если рассматривать стрельбу по достаточно большой круговой мишени, — пространством элементарных исходов будет круг, для удобства размещенный с центром в нуле, а исходом — точка в этом круге.
Кроме того, рассматривают множества элементарных исходов — события (например, попадание в «десятку» — это концентрический круг маленького радиуса с мишенью). В дискретном случае всё достаточно просто: мы можем получить любое событие, включая или исключая элементарные исходы за конечное время. В непрерывном же случае всё гораздо сложнее: нам понадобится некоторое достаточно хорошее семейство множеств для рассмотрения, называемое алгеброй по аналогии с простыми вещественными числами, которые можно складывать, вычитать, делить и умножать. Множества в алгебре можно пересекать и объединять, при этом результат операции будет находиться в алгебре. Это очень важное свойство для математики, которая лежит за всеми этими понятиями. Минимальное семейство состоит всего из двух множеств — из пустого множества и пространства элементарных исходов.
Мера и вероятность
Вместе совокупность множества элементарных исходов, семейства множеств и вероятностной меры называется вероятностным пространством. Рассмотрим, каким образом можно построить вероятностное пространство для примера со стрельбой в мишень.
Примечание На самом деле, это технический момент и в простых задачах процесс определения меры и семейства множеств не играет особой роли. Но понимать, что эти два объекта существуют, необходимо, ведь во многих книгах по теории вероятности теоремы начинаются со слов: «Пусть (Ω,Σ,P) — вероятностное пространство …».
Если предположить, что попадание в любую точку мишени равновероятно, поиск вероятности попадания стрелком в какую-то то область мишени сводится к поиску площади этого множества (отсюда можно сделать вывод, что вероятность попадания в конкретную точку нулевая, ведь площадь точки равна нулю).
Это одна из самых простых разновидностей задач на «геометрическую вероятность», — большинство таких задач требуют поиска площади.
Случайные величины
Средства абстракции от вероятностного пространства. Функция распределения и плотность
Функция распределения обладает несколькими свойствами:
Ещё одно полезное свойство плотности — вероятность того, что функция принимает значение из промежутка, вычисляется при помощи интеграла от плотности по этому промежутку (ознакомиться с тем, что это такое, можно в статьях о собственном, несобственном, неопределенном интегралах на сайте Mathprofi).
Следующее важное свойство плотности — интеграл от плотности любой случайной величины равен единице. Трактовка этого свойства такова: вероятность того, что функция принимает любое значение равна единице. Кроме того, при вычислении интегралов от плотностей случайных величин, значения которых лежат в ограниченном промежутке, нужно брать интеграл только по этому промежутку.
Итак, мы разобрались с несколькими важными понятиями: со строгим построением вероятностного пространства и построением случайных величин на нём. Кроме того, мы научились абстрагироваться от конкретного вероятностного пространства при помощи функции распределения и плотности.
«Программирование для начинающих» + теория вероятностей
Интересное дело: любой видео-курс по программированию, от PHP до Java, включает в себя главу для начинающих — чаще всего в ней рассказывается об азах структурного программирования: переменных, ветвлениях и циклах.
Поэтому мы решили раз и навсегда решить эту проблему — и сняли курс «Программирование для начинающих», который поможет самым новичкам понять и разобраться с этими базовыми понятиями, а также попробовать их в деле. Курс построен как серия видео-уроков на примере применения теории вероятностей (чтоб интереснее было).
В одном из первых видео объясняется, зачем вообще учиться программировать: вокруг всего так много только благодаря массовому производству, конвееру и автоматизации. Поэтому если мы не рабы, чтобы повторять тупую и нудную работу, то нужно учиться программировать — про это ещё Лейбниц сказал в XVII веке, только другими словами.
Курс сделан под язык JavaScript (как равноправного члена языков Си-семейства), и основы работы с ним студенты получают прямо в консоли браузера — удобно, ибо не надо ничего устанавливать.
Конечно, студенты этого курса не только постигнут теорию структурного программирования — им нужно дать пример какого-то простого проекта на закрепление полученных знаний.
Если вы думаете, что в это легко — взять и придумать пример проекта, когда из инструментария у тебя только переменные, условия и циклы, то это не совсем так. Вот что бы вы предложили? Учтите, что почти любое приложение предполагает ввод данных в той или иной форме — а этого мы решили в курсе не касаться. Так что ни тебе форм ввода, ни чтения из файла, ни запросов к базе данных.
Поэтому задачу придумали такую — сгенерировать беспроигрышную стратегию для игры в «Камень-ножницы-бумага», тогда за источник данных можно взять генератор случайных чисел. Если верить Википедии и университетскому курсу по теории вероятностей, то если при игре в «Камень-ножницы-бумагу» делать случайные ходы и играть очень много раз, то результат будет близок к ничьей (можете проверить на этом роботе).
Немножко скриншотов из курса
Переменные мы решили объяснять на яблоках. «У вас есть 2 яблока. Некто взял у вас одно яблоко. «, — говорит девочка с голубыми волосами. Эту простую задачу мы и взяли для того, чтобы проиллюстрировать факт, что у переменной есть постоянное имя и изменяемое значение. Переменные из повседневной жизни: курс доллара, цена барреля нефти, моя зарплата, сегодняшнее число, и т.д.
Условия тоже интуитивно понятны. «Красный — стой, зелёный — иди» — светофор как пример логики ветвления. 
Рисунок 1 — условие
Вот циклы могут быть понятны не всем. Хоть это и операция, требующая повторения тех же действий, но опыта программирования циклов у студентов нет. Поэтому подробно рассматриваются идеи счёта итераций и того, что случится, если цикл гонять бесконечно. 
Рисунок 2 — цикл
Итог программы визуально выглядит вот так (заодно и разобрались, что такое Unicodе-символы, и использовали их на практике): 
Рисунок 3 — программа генерации стратегии в «Камень-ножницы-бумага»
Надеюсь, мы не зря старались, и курс вам понравится! Эмм, уже говорил, что он бесплатный.
🎲 Зачем в науке о данных нужны теория вероятностей и статистика
С одной стороны, роль теории вероятностей и статистики в машинном обучении сравнительно невелика: используются лишь базовые понятия, хотя и довольно широко. С другой стороны, разведочный анализ данных, их очистка, подготовка и конструирование новых признаков – это чистая статистика. А поскольку эти операции в прикладной науке о данных (Data Science) занимают 90-95% времени, самый важный раздел математики для Data Scientist’ов – именно статистика. Кстати, это отлично демонстрирует разницу между машинным обучением и наукой о данных.
«Вероятности» классификации
Практически все модели классификации, используемые в машинном обучении, на самом деле выдают не единственную метку класса (или его номер), а набор «вероятностей» принадлежности к каждому классу. Логистическая регрессия с бинарной классификацией – это та же линейная регрессия, результат которой пропускается через функцию сигмоиды, преобразующую весь диапазон действительных чисел к диапазону [0,1].
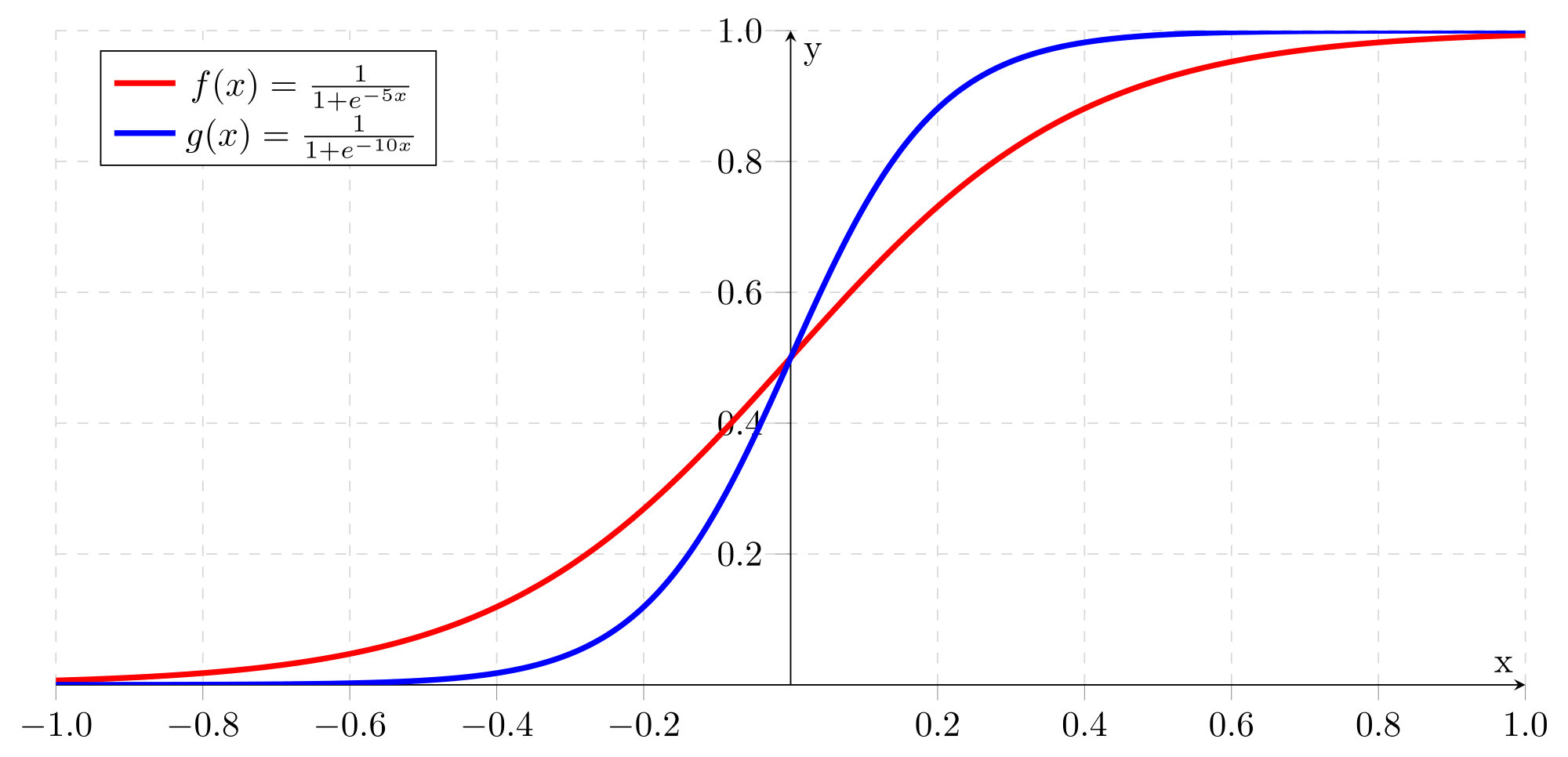
Число p, являющееся результатом сигмоиды, считается «вероятностью» принадлежности результата к одному из классов, а «вероятность» принадлежности к другому классу равна 1-p. Разумеется, это не настоящие вероятности – строго говоря, в данном случае вообще нет смысла говорить о вероятности, ведь результат классификации однозначен. Возможно, в данном случае было бы правильнее называть результат степенью уверенности: например, модель считает, что данный экземпляр принадлежит к классу 1 с уверенностью 74%. Тем не менее, принято называть этот показатель именно вероятностью.
Если классов больше двух, вместо сигмоиды используется Softmax – функция, преобразующая вектор вещественных чисел z размерности N в вектор неотрицательных чисел той же размерности, сумма которых равна 1 (sigma):
В результате мы получаем «вероятности» принадлежности к каждому классу, которые можно интерпретировать по-разному. Традиционно результатом классификации считается класс с максимальной «вероятностью», но ничто не мешает принять какие-то особые меры в тех случаях, когда модель «не уверена» в результате – например, если разница между двумя максимальными «вероятностями» невелика.
Если для классификации используется нейронная сеть, и классов больше двух, последним слоем этой сети практически всегда будет слой Softmax.
Все будет нормально
Нормальное распределение, или распределение Гаусса – это семейство функций плотности распределения вероятности с двумя параметрами: mu (среднее значение, оно же медиана и мода) и sigma (стандартное или среднеквадратическое отклонение). Иногда вместо sigma используется параметр sigma 2 – дисперсия нормального распределения:
График функции плотности нормального распределения похож на колокол. Его центральная координата равна mu, а стандартное отклонение sigma определяет уровень «крутизны» графика: чем оно меньше, чем большая доля значений переменной будет находиться недалеко от центра.
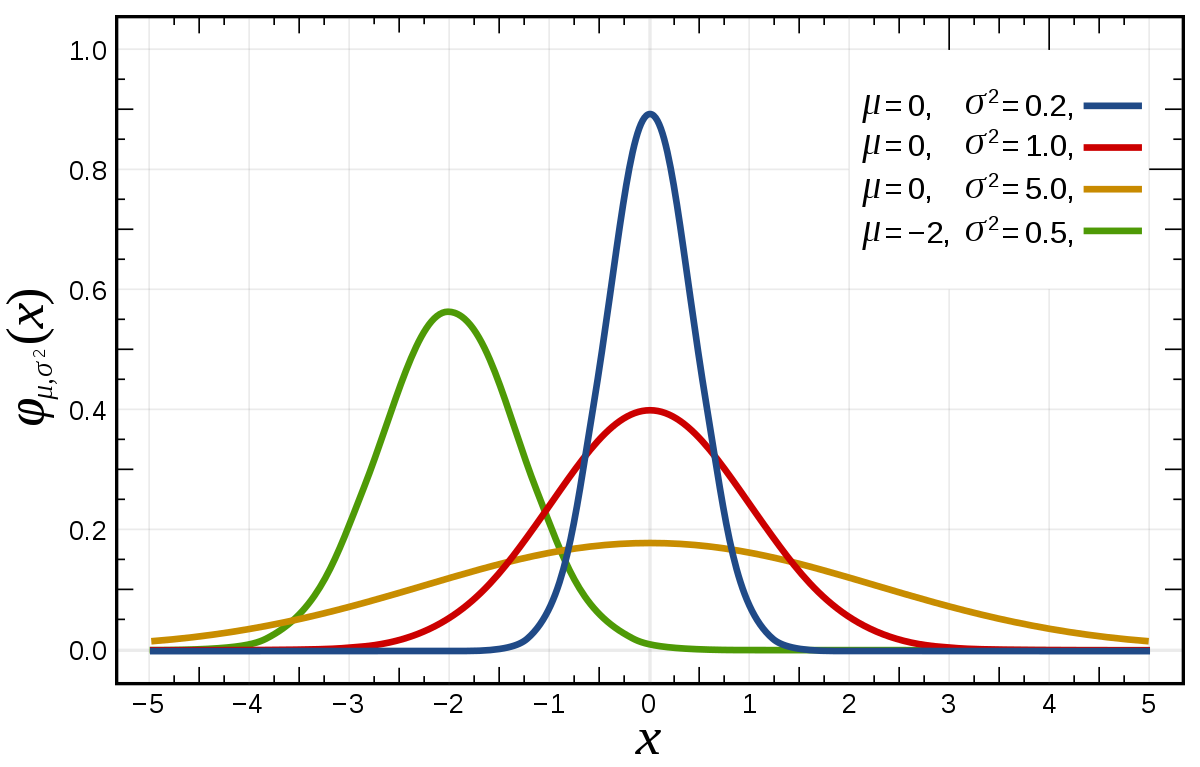
Центральная предельная теорема гласит, что сумма многих слабо зависимых друг от друга случайных величин имеет нормальное распределение – именно поэтому оно имеет огромное значение для статистики, которая обычно анализирует массовые явления. Например, если каждый человек, проходящий мимо кофейни, заходит выпить кофе с определенной вероятностью – то количество посетителей кафе будет иметь нормальное распределение.
Нормальное распределение настолько важно, что многие методы машинного обучения работают намного лучше, если данные нормально распределены (или даже вообще не работают в противном случае). Поэтому нормализация данных – очень часто выполняемая операция, а для нейронных сетей даже разработан слой пакетной нормализации (batch normalization).
Байесовские модели
Разведочный анализ данных
Разведочный анализ данных (exploratory data analysis, EDA) – это изучение данных для принятия решений по поводу их применения, очистки, преобразования и конструирования новых признаков. Как сказано выше, EDA – это чистая статистика, и основные цели его первого этапа – понять вид распределения признаков, основные параметры этого распределения, обнаружить выбросы и т.д.
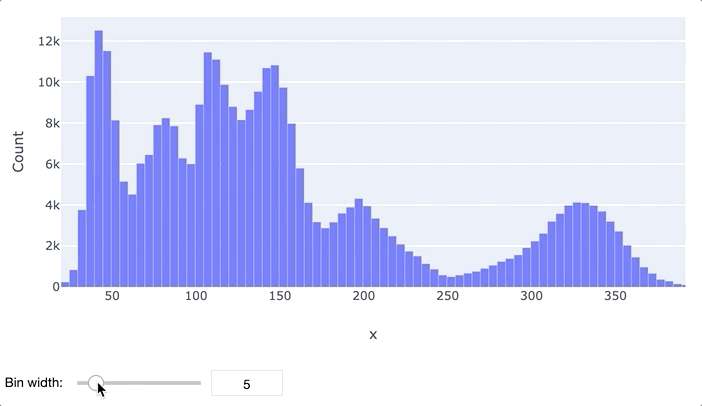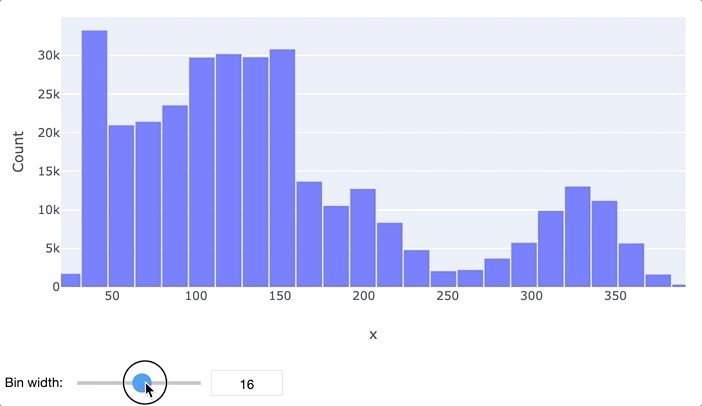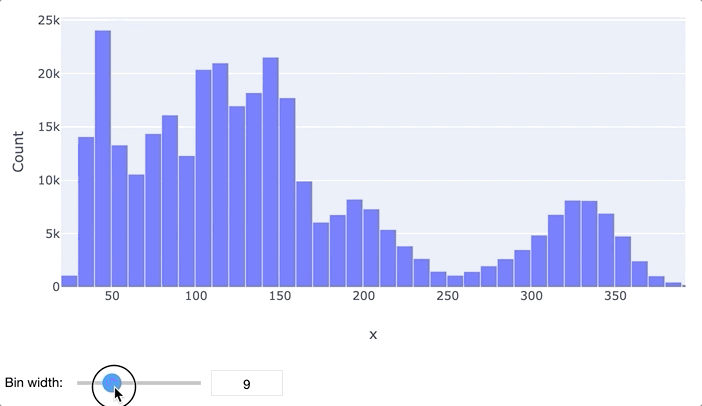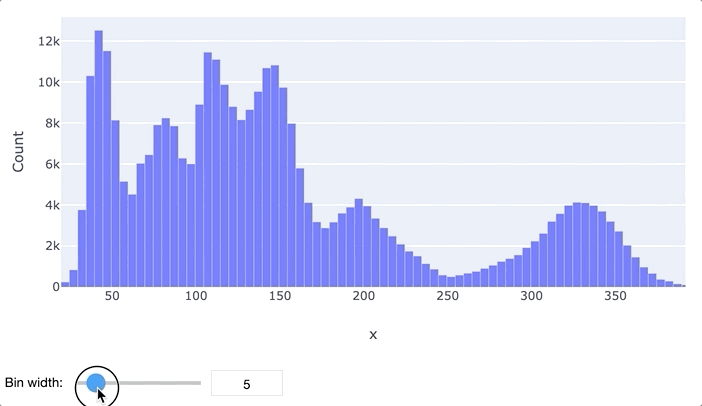
В первую очередь для анализа данных обычно применяются гистограммы и «ящики с усами». Гистограмма просто разбивает весь диапазон данных на несколько отрезков, и для каждого отрезка выводит количество элементов набора данных, попадающих в этот отрезок. Легко заметить, что гистограмма отдаленно похожа на график функции плотности распределения вероятности, так что по ней очень легко определить, распределен ли признак нормально или имеет какое-то иное распределение. Обычно выводятся гистограммы сразу для нескольких признаков.
«Ящик с усами» не позволяет увидеть общую картину распределения, зато предоставляет ценную информацию о его параметрах, особенно квантилях. Квантиль – это такое значение признака, что заданный процент значений этого признака в наборе данных меньше этого квантиля. Например, квантиль 50% – это такое значение, что половина значений признака меньше, а вторая половина – больше него, этот квантиль называется медианой. Квантили 0%, 25%, 50%, 75% и 100% называются квартилями, поскольку они делят область определения признака на четыре части.
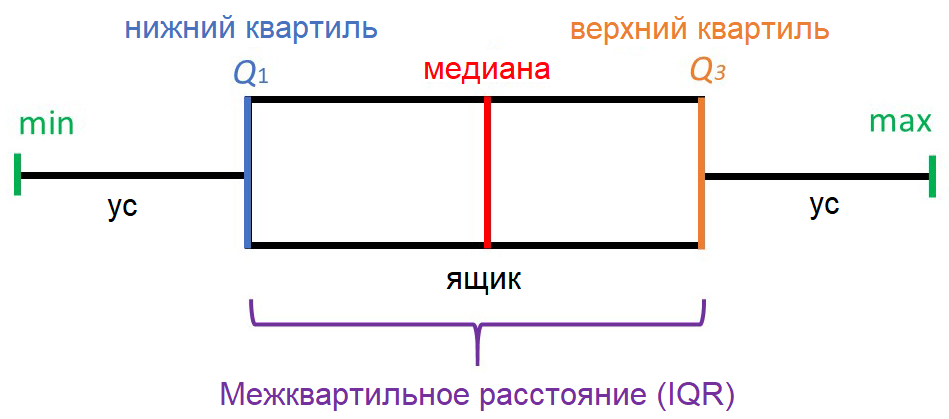
«Усы» выводятся без учета выбросов (outliers) – значений, больших Q3+1.5*IQR или меньших Q1-1.5*IQR. Принято считать, что выбросы скорее свидетельствуют об ошибках ввода данных, чем о реальных значениях признаков, и с ними надо что-то делать – например, удалить. На нашем рисунке выбросы не показаны, а в реальных «ящиках с усами» они выводятся в виде кружков за пределами «усов». Все понятия, о которых мы говорили, изучает статистика.
Анализ зависимостей между признаками
Для исследования возможных зависимостей между признаками используется множество методов, но самые простые из них – попарная диаграмма и матрица корреляции. Начнем с попарной диаграммы (pairplot). Выбираются несколько признаков, зависимости между которыми вы хотите исследовать, и получается комбинированная диаграмма, включающая небольшую диаграмму рассеяния (scatter plot) для каждой пары параметров. В диагональных клетках обычно выводятся графики или гистограммы соответствующих признаков.
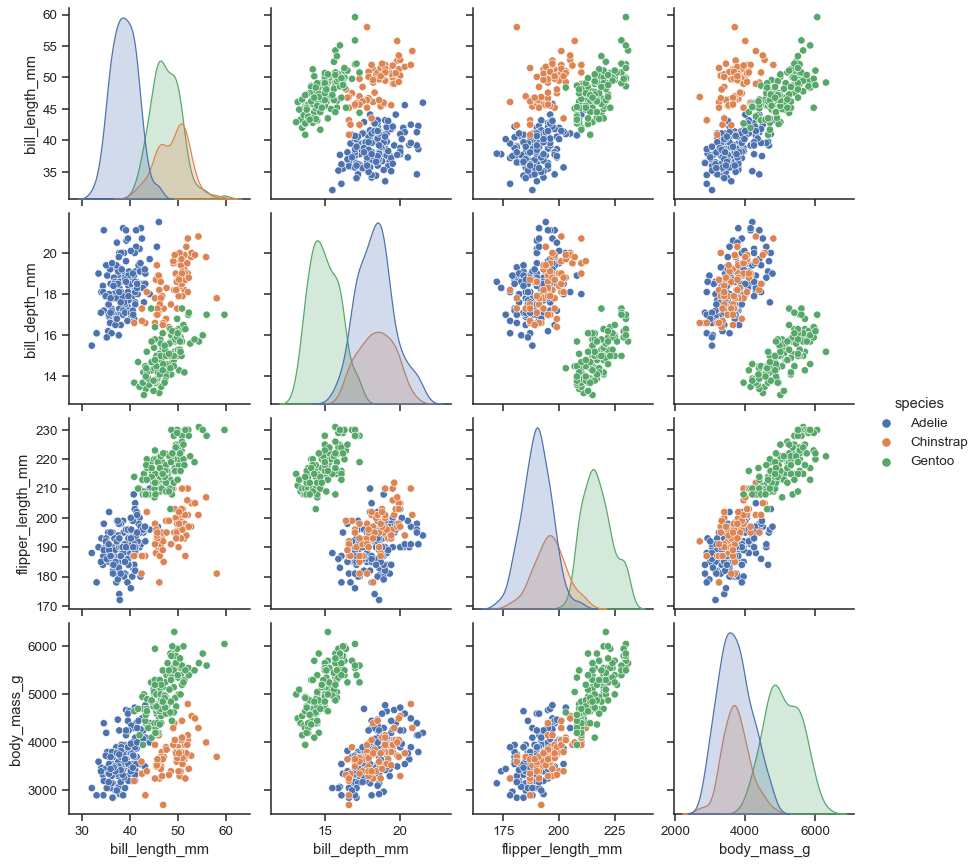
Коэффициент корреляции между двумя признаками x и y по набору данных, состоящему из n записей, считается следующим образом («x с крышкой» и «y с крышкой» – средние значения x и y):
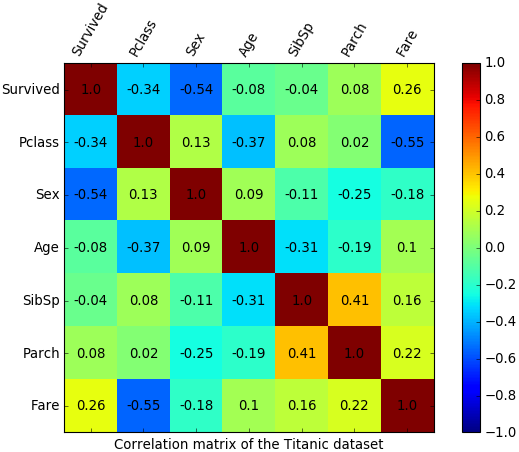
Например, из матрицы корреляции для набора данных о «Титанике» легко увидеть, что какая-то положительная корреляция есть только между количеством родителей и количеством детей на борту: люди плыли либо парами/в одиночку, либо целыми семьями. Отрицательная корреляция есть между пассажирским классом и ценой проезда (естественно, билеты низших по номеру классов стоили дороже) и между полом и признаком выжившего: мужчины уступали места в шлюпках дамам.
Заключение
Как мы уже говорили, статистика занимает особое место в науке о данных, поскольку все данные собираются и обрабатываются именно методами статистики. Более того, иногда вся работа Data Scientist’а, включая создание и усовершенствование моделей, проводится только для того, чтобы доказать или опровергнуть какую-нибудь статистическую гипотезу! А это значит, что каждый Data Scientist обязан знать статистику на профессиональном уровне – по крайней мере, именно такие требования к ним предъявляют на Западе. Помимо статистики придется освоить основы математического анализа и линейной алгебры, о которых шла речь в первых публикациях нашего небольшого цикла.
Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.