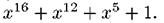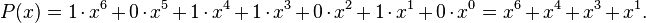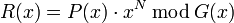вычисление циклического контрольного кода
Циклический избыточный код
Содержание
Введение
Помехоустойчивое кодирование
Первые попытки создания кодов с избыточной информацией начались задолго до появление современных ПК. К примеру, ещё в шестидесятых годах прошлого века Ридом и Соломоном была разработана эффективная методика кодирования — Код Рида-Соломона. Использование её в те времена не представлялось возможным, так как произвести операцию декодирования за разумное время первыми алгоритмами не удавалось. Точку в этом вопросе поставила фундаментальная работа Берлекампа, опубликованная в 1968 году. Эта методика, на практическое применение которой указал через год Мэсси, и по сей день используется в цифровых устройствах, обеспечивающих прием RS-кодированных данных. Более того: данная система позволяет не только определять позиции, но и исправлять неверные кодовые символы (чаще всего октеты).
Но далеко не везде от кода требуется коррекция ошибок. Многие современные каналы связи обладают приемлемыми характеристиками, и зачастую достаточно лишь проверить, успешно ли прошла передача или возникли какие-нибудь сложности; структура же ошибок и конкретные позиции неверных символов совершенно не интересуют принимающую сторону. И в этих условиях очень удачным решением оказались алгоритмы, использующие контрольные суммы. CRC как нельзя лучше подходит для подобных задач: невысокие затраты ресурсов, простота реализации и уже сформированный математический аппарат из теории линейных циклических кодов обеспечили ей огромную популярность.
Контрольная сумма
В самом общем своем виде контрольная сумма представляет собой некоторое значение, построенное по определенной схеме на основе кодируемого сообщения. Проверочная информация при систематическом кодировании дописывается в конец сообщения — после полезных данных. На принимающей стороне абонент знает алгоритм вычисления контрольной суммы: соответственно, программа имеет возможность проверить корректность принятых данных.
При передаче пакетов по реальному каналу, разумеется, могут возникнуть искажения исходной информации вследствие разных внешних воздействий: электрических наводок, плохих погодных условий и многих других. Сущность методики в том, что при хороших характеристиках хэш-функции в подавляющем числе случаев ошибка в сообщении приведет к изменению вычисленного на приеме значения CRC. Если исходная и вычисленная суммы не равны между собой, принимается решение о недостоверности принятых данных, и можно запросить повторную передачу пакета.
Математическое описание
Алгоритм CRC базируется на свойствах деления с остатком двоичных многочленов, то есть многочленов над конечным полем 
. Значение CRC является по сути остатком от деления многочлена, соответствующего входным данным, на некий фиксированный порождающий многочлен.
Каждой конечной последовательности битов 
взаимно однозначно сопоставляется двоичный полином 
, последовательность коэффициентов которого представляет собой исходную последовательность. Например, последовательность битов 1011010 соответствует многочлену:
Количество различных многочленов степени меньшей 
равно 
, что совпадает с числом всех двоичных последовательностей длины .
Значение контрольной суммы в алгоритме с порождающим многочленом G(x) степени N определяется как битовая последовательность длины N, представляющая многочлен R(x), получившийся в остатке при делении многочлена P(x), представляющего входной поток бит, на многочлен G(x):
— многочлен, представляющий значение CRC. 
— многочлен, коэффициенты которого представляют входные данные. 
— порождающий многочлен. — степень порождающего многочлена.
Умножение 
осуществляется приписыванием нулевых битов к входной последовательности, что улучшает качество хеширования для коротких входных последовательностей.
При делении с остатком исходного многочлена на порождающий полином G(x) степени N можно получить 2 N различных остатков от деления. G(x) всегда является неприводимым многочленом. Обычно его подбирают в соответствии с требованиями к хэш-функции в контексте каждого конкретного применения.
Тем не менее, существует множество стандартизированных образующих многочленов, обладающих хорошими математическими и корреляционными свойствами (минимальное число коллизий, простота вычисления). В статье приведены некоторые из них, а также соответствующие реализации на языке Си.
Вычисление CRC
Параметры алгоритма
Говоря о формировании контрольной суммы CRC, в первую очередь нужно упомянуть о полиноме-генераторе. Существует огромное множество многочленов, участвующих в формировании cyclic reduntancy code; многие из них указаны в конце статьи.
Другим параметром конкретного алгоритма вычисления контрольной суммы является размер слова, или суммарное количество регистров — информационных ячеек, используемых для вычисления численного значения хэша. При этом обязательно учитывается то, что размер слова и степень образующего контрольную сумму полинома совпадают. На практике более всего распространены 8, 16 и 32 — битовые слова, что является следствием особенностей архитектуры современной вычислительной техники.
И последний параметр, важный при описании определенной методики — начальные состояния регистров (стартовое слово). Это последняя из трех значимых характеристик; зная их в совокупности, мы можем восстановить алгоритм вычисления CRC, если данная модификация методики не имеет специфических особенностей, таких, как обратный порядок обработки битов.
Описание процедуры
Из файла берется первое слово — это может быть битовый (CRC-1), байтовый (CRC-8) или любой другой элемент. Если старший бит в слове «1», то слово сдвигается влево на один разряд с последующим выполнением операции XOR. Соответственно, если старший бит в слове «0», то после сдвига операция XOR не выполняется. После сдвига теряется старый старший бит, а младший бит освобождается — его значение устанавливается равным нулю. На место младшего бита загружается очередной бит из файла, и операция повторяется до тех пор, пока не загрузится последний бит файла. После прохождения всего файла, в слове остается остаток, который и является контрольной суммой.
Наиболее используемые и стандартизованные полиномы
В то время, как циклические избыточные коды являются частью стандартов, у этого термина не существует общепринятого определения — трактовки различных авторов нередко противоречат друг другу. [1] [5]
При этом многие широко используемые полиномы не являются наиболее эффективными из всех возможных. В 1993—2004 годах группа ученых занималась исследованием порождающих многочленов разрядности до 16, [1] 24 и 32 бит, [6] [7] и нашла полиномы, дающие лучшую, нежели стандартизированные многочлены, производительность в смысле кодового расстояния. [7] Один из результатов этого исследования уже нашёл своё применение в протоколе iSCSI.
Ниже в таблице перечислены наиболее распространенные многочлены — генераторы CRC.На практике вычисление CRC может включать пре- и пост-инверсию, а также обратный порядок обработки битов. В проприетарных реализациях CRC для усложнения анализа кода применяют ненулевые начальные значения регистров.
Существующие стандарты CRC-128 (IEEE) и CRC-256 (IEEE) в настоящее время вытеснены криптографическими хеш-функциями.
Попытки описания алгоритмов CRC
Примеры спецификаций некоторых алгоритмов CRC
Примеры программ для вычисления CRC на языке C
Разработка простых цифровых устройств
Разработка вычислителя контрольной суммы
Различные контрольные суммы широко применяются в цифровых устройствах и системах для контроля правильности хранения или передачи массивов информации. Суть этого метода контроля проста: к хранимому или передаваемому информационному массиву присоединяется небольшой контрольный код (обычно от 1 разряда до 32 разрядов), в котором в свернутом виде содержится информация обо всем массиве. При чтении или получении этого массива еще раз вычисляется тот же самый контрольный код по тому же самому алгоритму. Если этот вновь вычисленный код равен тому коду, который был присоединен к массиву, то считается, что массив сохранен или передан без ошибок. Логика здесь следующая: контрольный код (он же контрольная сумма ) гораздо меньше контролируемого массива, поэтому вероятность искажения контрольной суммы гораздо меньше, чем вероятность искажения массива. Если же исказятся как массив, так и контрольная сумма, то вероятность того, что эти искажения не будут замечены при повторном подсчете контрольной суммы, крайне мала. Существует, правда, вероятность, что массив будет искажен в нескольких местах таким образом, что контрольная сумма от этих искажений никак не изменится, но такая вероятность также обычно мала.
Контрольные суммы применяются при хранении данных в памяти (оперативной и постоянной), при хранении данных на магнитных носителях (дисках, лентах), в локальных и глобальных сетях передачи информации. В случае защиты контрольной суммой хранимой информации можно определить, что данный массив (файл, сектор на диске) испорчен и его нельзя использовать. В случае защиты контрольной суммой передаваемой по сети информации приемник может потребовать от передатчика повторной передачи искаженного массива.
Вычисляется циклическая контрольная сумма следующим образом. Весь массив информации рассматривается как одно N-разрядное двоичное число, где N — количество бит во всех байтах массива. Для вычисления контрольной суммы это N-разрядное число делится на некоторое постоянное число ( полином ), выбранное специальным образом (но делится не просто, а по модулю 2). Частное от этого деления отбрасывается, а остаток как раз и используется в качестве контрольной суммы.
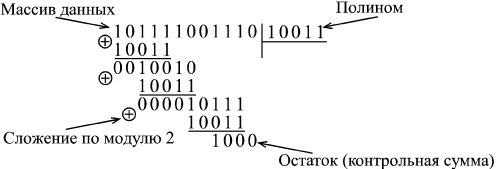
Деление по модулю 2 производится точно так же, как и привычное для нас деление «в столбик» (рис. 14.6), но вместо вычитания в данном случае используется поразрядное сложение по модулю 2, то есть каждый результирующий бит представляет собой функцию Исключающее ИЛИ от соответствующих битов слагаемых. Частное от деления нас не интересует, а остаток, равный в нашем примере 1000, и будет циклической контрольной суммой.
| Адрес в таблице | Данные в таблице (числа) |
|---|---|
| 0 | 0 |
| 1 | Остаток от деления числа 1 0000 0000 на полином |
| 2 | Остаток от деления числа 10 0000 0000 на полином |
| 3 | Остаток от деления числа 11 0000 0000 на полином |
| 4 | Остаток от деления числа 100 0000 0000 на полином |
| 5 | Остаток от деления числа 101 0000 0000 на полином |
 | |
| 255 | Остаток от деления числа 1111 1111 0000 0000 на полином |
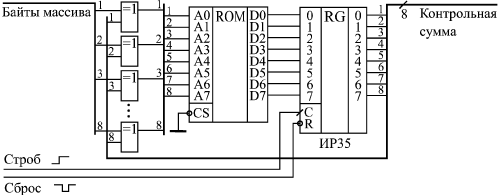
Числа представляют собой остаток от деления по модулю 2 числа с n конечными нулями (в нашем примере n = 8) и с n начальными разрядами, равными номеру числа (его адресу) в таблице. Деление производится на выбранный полином (в нашем случае — 9-разрядный). Таблица вычисляется один раз и хранится на диске или в ПЗУ.
Недостаток данной схемы параллельного вычислителя очевиден: в случае большого числа разрядов контрольной суммы требуется очень большой объем ПЗУ (64Кх16 для 16-разрядной суммы и 4Гх32 для 32-разрядной суммы). Поэтому она применяется сравнительно редко. Зато параллельный вычислитель обладает высоким быстродействием (байты могут поступать с периодом, равным сумме задержки выходного регистра, времени выборки адреса ПЗУ и задержки элемента Исключающее ИЛИ).
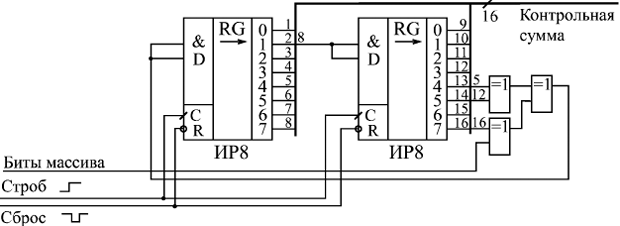
Для многоразрядной контрольной суммы чаще применяется другой подход — вычисление в последовательном коде, при котором массив данных поступает на вычислитель последовательно, бит за битом. Последовательный вычислитель контрольной суммы представляет собой сдвиговый регистр с обратными связями от некоторых разрядов через сумматоры по модулю 2 (то есть элементы Исключающее ИЛИ). Полное количество разрядов регистра сдвига должно быть равно разрядности вычисляемой контрольной суммы (или, что то же самое, быть на единицу меньше разрядности используемого полинома). Место включения обратных связей однозначно определяется выбранным полиномом. Это очень похоже на генератор квазислучайной последовательности.
Количество точек включения обратной связи определяется количеством единиц в полиноме (единица в младшем разряде не учитывается), а номера разрядов сдвигового регистра, с которых берутся сигналы обратной связи, определяются номерами единичных разрядов в коде полинома. В отличие от генератора квазислучайного сигнала, в данном случае необходимо смешать по функции Исключающее ИЛИ не только сигналы обратной связи, но и входной сигнал данных в последовательном коде.
Может показаться, что такой последовательный вычислитель не слишком удобен из-за того, что данные массива должны подаваться на него в последовательном коде. Однако именно в последовательном коде передаются данные в информационных сетях, и в последовательном коде записываются данные на магнитные носители. Поэтому во всех подобных случаях последовательные вычислители идеально подходят.
Период поступления битов массива на последовательный вычислитель не должен быть меньше суммы задержки регистра сдвига и элементов Исключающее ИЛИ. В итоге предельная скорость вычисления циклической контрольной суммы оказывается значительно меньшей, чем в случае параллельного вычислителя. Это также недостаток данного метода вычисления.
Циклические избыточные коды
Циклический избыточный код (Cyclical Redundancy Check — CRC) имеет фиксированную длину и используется для обнаружения ошибок. Наибольшее распространения получили коды CRC-16 и CRC-32, имеющие длину 16 и 32 бита соответственно. Код CRC строится по исходному сообщению произвольной длины, т.е. этот код не является блочным в строгом смысле этого слова. Но при каждом конкретном применении этот код — блочный, (m, m + 16)-код для CRC-16 или (m, m + 32)-код для CRC-32.
Вычисление значения кода CRC происходит посредством деления многочлена, соответствующего исходному сообщению (полином-сообщение), на фиксированный многочлен (полином-генератор). Остаток от такого деления и есть код CRC, соответствующий исходному сообщению. Для кода CRC-16 полином-генератор имеет степень 16, а для CRC-32 — 32. Полиномы-генераторы подбираются специальным образом и для кодов CRC-16/32 стандартизированы Международным консультативным комитетом по телеграфной и телефонной связи (CCITT). Для CRC-16, например, стандартным является полином-генератор
Пример построения CRC-4 кода для сообщения 11010111, используя полином-генератор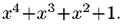
Исходному сообщению соответствует полином
x 7 + x 6 + x 4 + x 2 + x +1, т. е. нумерация битов здесь начинается справа.
Полиному х 2 + 1 соответствуют биты 0101 — это и есть CRC-4 код.
Существуют быстрые алгоритмы для расчета CRC-кодов, использующие специальные таблицы, а не деление многочленов с остатком.
CRC-коды способны обнаруживать одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга. При реальной передаче или хранении информации ошибки обычно группируются на некотором участке, а не распределяются равномерно по всей длине данных. Таким образом, хотя для идеального случая двоичного симметричного канала CRC-коды не имеют никаких теоретических преимуществ по сравнению, например, с простыми контрольными суммами, для реальных систем эти коды являются очень полезными.
Коды CRC используются очень широко: модемами, телекоммуникационными программами, программами архивации и проверки целостности данных и многими другими программными и аппаратными компонентами вычислительных систем.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Табличный метод вычисления CRC
Операция деление по модулю 2
Пусть массив (последовательность бит) имеет следующий вид: 101111001110 (для простоты примера берем небольшую разрядность). Число, на которое выполняется деление по модулю (носит название образующего полинома ) для примера будет 10011. Выбирается это число с учетом тех свойств, что оно должно делиться по модулю 2 без остатка только на единицу и само на себя. Образующий полином имеет разрядность на единицу больше чем разрядность контрольного кода. К примеру, если требуется получить 8 – разрядный контрольный код необходимо взять образующий полином 9 – разрядный.
В рассматриваемом примере это полином 5-го разряда, а контрольная сумма (остаток от деления) будет 4-х разрядной. Если бы требовалось получить 8-разрядный остаток то можно, к примеру, было бы взять образующий полином равным 100011101 в шестнадцатеричном коде 11D.
Операция деления по модулю два выполняется практически так же как обычное деление в столбик (рис. 1), но вместо вычитания выполняется поразрядное сложение по модулю 2, где каждый полученный бит есть результат выполнения функции исключающее ИЛИ (XOR) от соответствующих слагаемых битов. Остаток от деления в данном примере 1000 есть циклическая контрольная сумма (частное отбрасывается).
Реализация на практике вычисления циклического контрольного кода, выполняется параллельным и последовательным методами. Практическая реализация вычисления этого остатка возможна по приведенному здесь примеру аппаратным или программным способом, но этот способ считается медленным. Увеличить скорость вычисления контрольного кода можно, прибегнув, к так называемому табличному методу. Суть метода такова создается таблица чисел размером 2 n хn, где n — разрядность контрольной суммы. Метод вычисления чисел в таблице следующий (табл. 1).
Таблица 1. Табличный метод вычисления контрольной суммы.
| Адрес в таблице | Данные в таблице (числа) |
| Остаток от деления числа 1 0000 0000 на полином | |
| Остаток от деления числа 10 0000 0000 на полином | |
| Остаток от деления числа 11 0000 0000 на полином | |
| Остаток от деления числа 100 0000 0000 на полином | |
| Остаток от деления числа 101 0000 0000 на полином | |
| … | |
| Остаток от деления числа 1111 1111 0000 0000 на полином |
Числа являются остатком от деления по модулю 2 числа с n конечными нулями (в нашем примере n = 8) и с n начальными разрядами, равными номеру числа (его адресу) в таблице. Выполняется деление на 9-разрядный образующий полином. Вычисление таблицы производится однократно, и она хранится в ПЗУ или на диске.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Циклический избыточный код
Циклический избыточный код
Циклический избыточный код (англ. Cyclic redundancy check, CRC) — алгоритм нахождения контрольной суммы, предназначенный для проверки целостности данных. CRC является практическим приложением помехоустойчивого кодирования, основанном на определённых математических свойствах циклического кода.
Понятие циклические коды достаточно широкое. В англоязычной литературе CRC расшифровывается двояко в зависимости от контекста: Cyclic Redundancy Code или Cyclic Redundancy Check. Под первой расшифровкой понимают математический феномен циклических кодов, под второй — конкретное применение этого феномена как хэш-функции.
Первые попытки создания кодов с избыточной информацией начались задолго до появления современных компьютеров. К примеру, ещё в 1960-х годахРидом и Соломоном была разработана эффективная методика кодирования — Код Рида-Соломона. Использование её в те времена не представлялось возможным, так как произвести операцию декодирования за разумное время первыми алгоритмами не удавалось. Точку в этом вопросе поставила фундаментальная работа Берлекампа, опубликованная в 1968 году. Эта методика, на практическое применение которой указал через год Мэсси, и по сей день используется в цифровых устройствах, обеспечивающих приём RS-кодированных данных. Более того: данная система позволяет не только определять позиции, но и исправлять неверные кодовые символы (чаще всего октеты).
Но далеко не всегда от кода требуется коррекция ошибок. Многие современные каналы связи обладают приемлемыми характеристиками, и зачастую достаточно лишь проверить, успешно ли прошла передача или возникли какие-нибудь сложности; структура же ошибок и конкретные позиции неверных символов совершенно не интересуют принимающую сторону. И в этих условиях очень удачным решением оказались алгоритмы, использующие контрольные суммы. CRC как нельзя лучше подходит для подобных задач: невысокие затраты ресурсов, простота реализации и уже сформированный математический аппарат из теории линейных циклических кодов обеспечили ей огромную популярность.
В общем виде контрольная сумма представляет собой некоторое значение, вычисленное по определённой схеме на основе кодируемого сообщения. Проверочная информация при систематическом кодировании приписывается к передаваемым данным. На принимающей стороне абонент знает алгоритм вычисления контрольной суммы: соответственно, программа имеет возможность проверить корректность принятых данных.
При передаче пакетов по сетевому каналу могут возникнуть искажения исходной информации вследствие разных внешних воздействий: электрических наводок, плохих погодных условий и многих других. Сущность методики в том, что при хороших характеристиках контрольной суммы в подавляющем числе случаев ошибка в сообщении приведёт к изменению его контрольной суммы. Если исходная и вычисленная суммы не равны между собой, принимается решение о недостоверности принятых данных, и можно запросить повторную передачу пакета.
Алгоритм CRC базируется на свойствах деления с остатком двоичных многочленов, то есть многочленов над конечным полем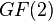 
. Значение CRC является по сути остатком от деления многочлена, соответствующего входным данным, на некий фиксированный порождающий многочлен.
Каждой конечной последовательности битов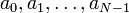 
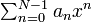
взаимно однозначно сопоставляется двоичный полином 
, последовательность коэффициентов которого представляет собой исходную последовательность. Например, последовательность битов 1011010 соответствует многочлену:
Количество различных многочленов степени меньшей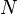 
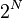
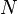
равно 
, что совпадает с числом всех двоичных последовательностей длины 
.
Значение контрольной суммы в алгоритме с порождающим многочленом G(x) степени N определяется как битовая последовательность длины N, представляющая многочлен R(x), получившийся в остатке при делении многочлена P(x), представляющего входной поток бит, на многочлен G(x):
— многочлен, представляющий значение CRC;
— многочлен, коэффициенты которого представляют входные данные;
— порождающий многочлен;
— степень порождающего многочлена.
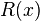
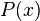
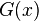
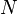
Умножение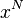 
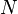
осуществляется приписыванием 
нулевых битов к входной последовательности, что улучшает качество хеширования для коротких входных последовательностей.
При делении с остатком исходного многочлена на порождающий полином G(x) степени N можно получить 2 N различных остатков от деления. G(x) зачастую является неприводимым многочленом. Обычно его подбирают в соответствии с требованиями к хэш-функции в контексте каждого конкретного применения. Тем не менее, существует множество стандартизированных образующих многочленов, обладающих хорошими математическими и корреляционными свойствами (минимальное число коллизий, простота вычисления), некоторые из которых перечислены ниже.
Схема формирования контрольной суммы CRC-8. Порождающий многочлен g(x) = x8+x5+x4+1
Одним из основных параметров CRC является порождающий полином.
С порождающим полиномом связан другой параметр — его степень, которая определяет количество битов, используемых для вычисления значения CRC. На практике наиболее распространены 8-ми, 16-ти и 32-х битовые слова, что является следствием особенностей архитектуры современной вычислительной техники.
Ещё одним параметром является начальное (стартовое) значение слова. Указанные параметры полностью определяют «традиционный» алгоритм вычисления CRC. Существуют также модификации алгоритма, например, использующие обратный порядок обработки битов.