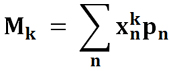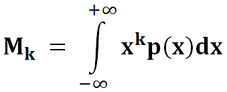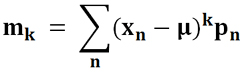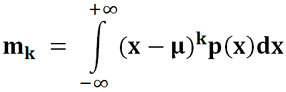указать верное определение мода распределения это
Тест с ответами по теории вероятности
1.Указать верное определение.Суммой двух событий называется:
а ) Новое событие, состоящее в том, что происходят оба события одновменно;
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;+
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
а ) Новое событие, состоящее в том, что происходят оба события одновременно;+
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
а ) Произведение числа исходов, благоприятствующих появлению события на общее число исходов;
б ) Сумма числа исходов, благоприятствующих появлению события и общего числа исходов;
в ) Отношение числа исходов, благоприятствующих появлению события к общему числу исходов;+
а ) больше нуля и меньше единицы;
а ) больше нуля и меньше единицы;
а ) больше нуля и меньше единицы;+
а ) Вероятность суммы событий равна сумме вероятностей этих событий;
б ) Вероятность суммы независимых событий равна сумме вероятностей этих событий;
в ) Вероятность суммы несовместных событий равна сумме вероятностей этих событий;+
а ) Вероятность произведения событий равна произведению вероятностей этих событий;
б ) Вероятность произведения независимых событий равна произведению вероятностей этих событий;+
в ) Вероятность произведения несовместных событий равна произведению вероятностей этих событий;
а ) Элементарный исход;
б ) Пространство элементарных исходов;
в ) Подмножество множества элементарных исходов.+
а ) любые попарно несовместные события;
б ) попарно несовместные события, объединение которых образует достоверное событие;+
в ) пространство элементарных событий.
а ) априорную вероятность гипотезы,
б ) апостериорную вероятность гипотезы,
в ) вероятность гипотезы.+
а) невозрастающей; б) неубывающей; +в) произвольного вида.
а) независимых+; б) зависимых; в) всех.
а) независимых;+ б) зависимых; в) всех.
а) отсутствует функциональная зависимость между Х и Y;
б) величины Х и Y независимы;+
в) отсутствует линейная корреляция между Х и Y;
а) указывая её вероятности;
б) указывая её закон распределения;+
в) поставив каждому элементарному исходу в соответствие
а) начальный момент первого порядка;+
б) центральный момент первого порядка;
в) произвольный момент первого порядка.
а) начальный момент второго порядка;
б) центральный момент второго порядка;+
в) произвольный момент второго порядка.
а) значение случайной величины при котором вероятность равняется 0,5;
б) значение случайной величины при котором либо вероятность, либо функция плотности достигают максимального значения ;+
в) значение случайной величины при котором вероятность равняется 0.
а) если все варианты увеличить в одно и тоже число раз, то и дисперсия увеличится в такое же число раз.
б) дисперсия постоянной равняется нулю.
в) если все варианты увеличить на одно и тоже число, то выборочная дисперсия не изменится.+
а) Представление наблюдений в качестве независимых случайных величин имеющих один и тот же закон распределения.
б) совокупность результатов наблюдений;
в) всякую функцию результатов наблюдения.+
а) Метод максимального правдоподобия используется для получения оценок;
б) Выборочная дисперсия является смещенной оценкой для дисперсии;
в) В качестве статистических оценок параметров используются несмещённые, несостоятельные, эффективные оценки.+
а) По многомерной функции распределения всегда можно найти одномерные (маргинальные) распределения отдельных компонент.
б) По одномерным (маргинальным) распределениям отдельных компонент всегда можно найти многомерную функцию распределения.
в) По многомерной функции плотности всегда можно найти одномерные (маргинальные) плотности распределения отдельных компонент.
а) Закон распределения случайной величины X не зависит от того, какое значение приняла случайная величина Y.
в) коэффициент корреляции между случайными величинами X и Y равен нулю.
а) аналогом формулы Байеса для непрерывных случайных величин;
б) аналогом формулы полной вероятности для непрерывных случайных величин;+
в) аналогом формулы произведения вероятностей независимых событий для непрерывных случайных величин.
а) выборка и группировка статистических данных, полученных в результате эксперимента;
б) определение параметров распределения, вид которого заранее известен;+
в) получение оценки вероятности изучаемого события.
Кто поможет решить тесты по теории вероятностей. 16 тестов. ОТпишитесь кто может помочь.
1.Указать верное определение. Суммой двух событий называется:
а ) Новое событие, состоящее в том, что происходят оба события одновменно;
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе; +
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
Указать верное определение. Произведением двух событий называется:
а ) Новое событие, состоящее в том, что происходят оба события одновременно; +
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
Указать верное определение. Вероятностью события называется:
а ) Произведение числа исходов, благоприятствующих появлению события на общее число исходов;
б ) Сумма числа исходов, благоприятствующих появлению события и общего числа исходов;
в ) Отношение числа исходов, благоприятствующих появлению события к общему числу исходов; +
Указать верное утверждение. Вероятность невозможного события:
а ) больше нуля и меньше единицы;
Указать верное утверждение. Вероятность достоверного события:
а ) больше нуля и меньше единицы;
Указать верное свойство. Вероятность случайного события:
а ) больше нуля и меньше единицы; +
Указать правильное утверждение:
а ) Вероятность суммы событий равна сумме вероятностей этих событий;
б ) Вероятность суммы независимых событий равна сумме вероятностей этих событий;
в ) Вероятность суммы несовместных событий равна сумме вероятностей этих событий; +
Указать правильное утверждение:
а ) Вероятность произведения событий равна произведению вероятностей этих событий;
б ) Вероятность произведения независимых событий равна произведению вероятностей этих событий; +
в ) Вероятность произведения несовместных событий равна произведению вероятностей этих событий;
Указать верное определение. Событие это:
а ) Элементарный исход;
б ) Пространство элементарных исходов;
в ) Подмножество множества элементарных исходов. +
Указать правильный ответ. Какие события называются гипотезами?.
а ) любые попарно несовместные события;
б ) попарно несовместные события, объединение которых образует достоверное событие; +
в ) пространство элементарных событий.
Указать правильный ответ Формулы Байеса определяют:
а ) априорную вероятность гипотезы,
б ) апостериорную вероятность гипотезы,
в ) вероятность гипотезы. +
Указать верное свойство. Функция распределения случайной величины Х является:
а) невозрастающей; б) неубывающей; +в) произвольного вида.
Указать верное свойство. Равенство справедливо для случайных величин:
а) независимых+; б) зависимых; в) всех.
Указать верное свойство. Равенство справедливо для случайных величин:
а) независимых; + б) зависимых; в) всех.
Указать правильное заключение. Из того, что корреляционный момент для двух случайных величин Х и Y равен нулю следует:
а) отсутствует функциональная зависимость между Х и Y;
б) величины Х и Y независимы; +
в) отсутствует линейная корреляция между Х и Y;
Указать правильный ответ. Дискретную случайную величину задают:
а) указывая её вероятности;
б) указывая её закон распределения; +
в) поставив каждому элементарному исходу в соответствие
Указать верное определение. Математическое ожидание случайной величины — это:
а) начальный момент первого порядка; +
б) центральный момент первого порядка;
в) произвольный момент первого порядка.
Указать верное определение. Дисперсия случайной величины- это:
а) начальный момент второго порядка;
Тест с ответами по Теории вероятности (Указать верное определение …)
1.Указать верное определение. Суммой двух событий называется:
а ) Новое событие, состоящее в том, что происходят оба события одновменно;
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;+
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
а ) Новое событие, состоящее в том, что происходят оба события одновременно;+
б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;
в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.
а ) Произведение числа исходов, благоприятствующих появлению события на общее число исходов;
б ) Сумма числа исходов, благоприятствующих появлению события и общего числа исходов;
в ) Отношение числа исходов, благоприятствующих появлению события к общему числу исходов;+
а ) больше нуля и меньше единицы;
а ) больше нуля и меньше единицы;
а ) больше нуля и меньше единицы;+
а ) Вероятность суммы событий равна сумме вероятностей этих событий;
б ) Вероятность суммы независимых событий равна сумме вероятностей этих событий;
в ) Вероятность суммы несовместных событий равна сумме вероятностей этих событий;+
а ) Вероятность произведения событий равна произведению вероятностей этих событий;
б ) Вероятность произведения независимых событий равна произведению вероятностей этих событий;+
в ) Вероятность произведения несовместных событий равна произведению вероятностей этих событий;
а ) Элементарный исход;
б ) Пространство элементарных исходов;
в ) Подмножество множества элементарных исходов.+
а ) любые попарно несовместные события;
б ) попарно несовместные события, объединение которых образует достоверное событие;+
в ) пространство элементарных событий.
а ) априорную вероятность гипотезы,
б ) апостериорную вероятность гипотезы,
в ) вероятность гипотезы.+
а) невозрастающей; б) неубывающей; +в) произвольного вида.
а) независимых+; б) зависимых; в) всех.
а) независимых;+ б) зависимых; в) всех.
а) отсутствует функциональная зависимость между Х и Y;
б) величины Х и Y независимы;+
в) отсутствует линейная корреляция между Х и Y;
а) указывая её вероятности;
б) указывая её закон распределения;+
в) поставив каждому элементарному исходу в соответствие
а) начальный момент первого порядка;+
б) центральный момент первого порядка;
в) произвольный момент первого порядка.
б) центральный момент второго порядка;+
в) произвольный момент второго порядка.
а) значение случайной величины при котором вероятность равняется 0,5;
б) значение случайной величины при котором либо вероятность, либо функция плотности достигают максимального значения ;+
в) значение случайной величины при котором вероятность равняется 0.
а) если все варианты увеличить в одно и тоже число раз, то и дисперсия увеличится в такое же число раз.
б) дисперсия постоянной равняется нулю.
в) если все варианты увеличить на одно и тоже число, то выборочная дисперсия не изменится.+
а) Представление наблюдений в качестве независимых случайных величин имеющих один и тот же закон распределения.
б) совокупность результатов наблюдений;
в) всякую функцию результатов наблюдения.+
а) Метод максимального правдоподобия используется для получения оценок;
б) Выборочная дисперсия является смещенной оценкой для дисперсии;
в) В качестве статистических оценок параметров используются несмещённые, несостоятельные, эффективные оценки.+
а) По многомерной функции распределения всегда можно найти одномерные (маргинальные) распределения отдельных компонент.
б) По одномерным (маргинальным) распределениям отдельных компонент всегда можно найти многомерную функцию распределения.
в) По многомерной функции плотности всегда можно найти одномерные (маргинальные) плотности распределения отдельных компонент.
а) Закон распределения случайной величины X не зависит от того, какое значение приняла случайная величина Y.
в) коэффициент корреляции между случайными величинами X и Y равен нулю.
а) аналогом формулы Байеса для непрерывных случайных величин;
б) аналогом формулы полной вероятности для непрерывных случайных величин;+
в) аналогом формулы произведения вероятностей независимых событий для непрерывных случайных величин.
а) выборка и группировка статистических данных, полученных в результате эксперимента;
б) определение параметров распределения, вид которого заранее известен;+
в) получение оценки вероятности изучаемого события.
Мода в статистике
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Распределения и моменты
Закон распределения случайной величины
Для характеристики вероятности появления различных значений случайной величины используют законы распределения вероятностей случайной величины. При этом используют два вида представления законов распределения: интегральный и дифференциальный.
Интегральный закон, или функция распределения вероятностей случайной величины X, называется функция, значение которой для любого x является вероятностью события, заключающегося в том, что случайная величина X принимает значения, меньшие x, то есть функция F(x)=P
Рассмотрим типичную задачу по вычислению математического ожидания на бинарных опционах. Допустим, брокер на выигрыш выплачивает 75% от размера ставки, а на проигрыш забирает всю ставку 100%. Найдем матожидание для метода прогнозирования, который дает 65% успешных сделок.
Собираем это всё в сумму по формуле математического ожидания для дискретного распределения и получаем.
Положительное математическое ожидание говорит о том, что данный метод прогнозирования можно использовать на бинарных опционах. Трейдер будет в прибыли при большом количестве сделанных ставок, теоретически при бесконечном числе ставок (и если у него хватит начального депозита на просадки в серии проигрышей).
А если метод прогнозирования трейдера дает только 65% прибыльных сделок?
В этом случае p=0.55, q=0.45. Подставляя эти данные в формулу математического ожидания для дискретного распределения, получаем μ=-0.0375.
Отрицательное матожидание говорит о том, что данный метод прогнозирования ни в коем случае нельзя применять. Если с таким методом прогнозирования трейдер получил прибыль на конечной серии ставок, то это простое случайное везение.
Формула математического ожидания позволяет найти пограничное значение доли прибыльных сделок, которое необходимо получить от метода прогнозирования, и вывести основную формулу бинарных опционов. Основная формула бинарных опционов соответствует нулевому математическому ожиданию.
На Форексе и на фондовой бирже всё вычисляется аналогично. С той лишь разницей, что там параметры α и ß определяются через положения ордеров TakeProfit и StopLoss. Суть параметров α и ß, это доли прибыли и убытка от размера собственных средств трейдера, участвующих в сделке.
Моменты распределения
Начальный момент k-го порядка вычисляется по следующим формулам.
Для дискретного распределения:
Для непрерывного распределения:
Нулевой начальный момент всегда равен единице, так как эти формулы при k=0 переходят в условия нормировки. А первый начальный момент (k=1), это как раз и есть математическое ожидание, о котором говорилось выше.
Центральный момент k-го порядка вычисляется по следующим формулам.
Для дискретного распределения:
Для непрерывного распределения:
Для центральных моментов также нулевой момент всегда равен единице. А первый центральный момент всегда равен нулю. Мы, как бы, делаем такой параллельный перенос, при котором точка математического ожидания переходит в точку ноль.