статистика медиана мода среднее
Статистика медиана мода среднее
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
Среднее значение, медиана и мода
Эти три термина являются основными показателями в статистическом анализе. Если 20 лет назад в нашей стране они интересовали только экономистов и работников статистики, то теперь почти каждый, кто имеет хоть какое-либо отношение к коммерции, следит за этими данными. Это работники банковского сектора, торговли, сервиса о больше всех брокеры.
Но в этой статье мы не будем подробно объяснять каждый из этих терминов. Их достаточно распиарили и без нас. Вместо этого остановимся на объяснении этих трех терминов: среднее значение, медиана и мода. Все три термина объясним с примерами.
Среднее значение
Часто так называют среднеарифметическое значение выборки (или множества чисел). Это, пожалуй, самый распространенный термин, из вышеперечисленных трех. Хотя бы потому, что почти каждый день мы слышим это слово в СМИ. Значение его тоже объясняет само название. Тем не менее, для тех, кому непонятен смысл этого слова, объясним “на пальцах”.
Это сумма данных чисел, деленное на количество. Если написать в виде формулы, это выглядит так.
Пример из практики
Медиана
Медиана – число, характеризующее выборку, т.е. если взять все элементы множества, то это число ровно делит множество пополам. Одна половина множества равна или больше этого число, а другая меньше или равна этому числу.
Пример из практики
Значит, среднее значение в год составляет
$(1,000,000 + 200,000 + 8,900) : 100 = 1,208,900 : 100 = 12,089$ у.е.
Зная соотношение неработающих людей, на каждого работающего, и поделив полученное на это число, получим доход на душу населения (с учетом детей, стариков и больных без пенсии).
Итак, такая статистика показывает, что народ живет припеваючи, зарабатывая примерно 1,000 у.е. в месяц, а действительность другая. Как раз, так и вычисляется доход на душу населения. Берется национальный доход и делится на численность населения. Теперь вы понимаете, почему в сводках всегда называют эту цифру, потому что она никоим образом не отображает благосостояние большинства, а только является показателем экономического благосостояния страны.
Пример из практики
Если постоять на проспекте и в течение 10 минут и посчитать все проезжающие автомобили и классифицировать их по цветам, то можно определить моду для цвета автомобилей этого города. Допустим, насчитали 95 белых, 45 черных, 12 красных, 38 серых и 70 других цветов. Значит, модой в этом городе являются автомобили белого цвета. Это хорошая информация для дистрибьюторов автомобилей.
Подробнее о среднем значении
Иногда вычисляют среднее значение для группы данных. Тогда значения разбивают на группы и вычисляют серединную точку каждой группы. Затем эти значения умножают на количество членов каждой группы (на частотность) и складывают. А результат делят на общее количество. Такое значение называют средним значением группы. Посмотрите на этот пример:
| Группа | Частота | Середина |
|---|---|---|
| 1-20 | 5 | 10.5 |
| 21-40 | 25 | 30.5 |
| 41-60 | 37 | 50.5 |
| 61-80 | 23 | 70.5 |
Умножаем эти значения на частоты и складываем, затем делим на общее количество:
Как уже показали на примере с доходом населения, экстремумы сильно влияют на среднеарифметическое значение, поэтому иногда полезно их отбрасывать. Тогда среднее значение называется урезанным средним.
В симметричном распределении (типа нормального распределения) среднее значение, медиана и мода равны или близки друг другу. В асимметричном же, они отличаются, и число, на которое отличаются эти показатели, дают информацию о “скошенности” распределения относительно нормального.
Надеемся, что нам удалось “на пальцах” объяснить значение терминов среднеарифметическое значение, медиана и мода. Если кто-то из Ваших знакомых до сих пор в недоумении, просвещайте их, поделившись данной статьей в соц. сетях.
Читайте также
Переменные потока и запасы
Все экономические переменные, которые имеют временное измерение, т.е. величины которых можно измерить по истечении времени называем переменными потока. А запас не имеет временное измерение.
Показатели вариации
Чтобы знать, насколько далеко значение совокупности простирается от центральной тенденции, вычисляют вариацию (на английском dispersion или variability, но не путайте с variation). Есть несколько показателей вариации. Это размах, межквартильный размах, среднее линейное отклонение, дисперсия и стандартное отклонение.
Типы выборки
Для расследования генеральной совокупности применяют два вида выборки. Случайную и неслучайную выборку. Простая, систематическая, стратифицированная и кластерная выборка являются случайными выборками. Стихийная, удобная и квотная выборка являются примером неслучайной выборки.
Скользящее среднее значение
Среди наиболее популярных технических индикаторов чаще всего, скользящее среднее значение используются для измерения направления текущего тренда. Самая простая формула скользящей средней, известна как Простое Скользящее Среднее значение.
Генеральная совокупность и выборка
Генеральной совокупностью называют всё исследуемое множество. На английском языке этот термин называется популяцией (population). Выборкой (на английском sample) называют некоторое случайно отобранное подмножество из генеральной совокупности.
Нулевая гипотеза
Нулевая гипотеза утверждает, что между исследуемыми данными никакой закономерности нет. Пока нулевая гипотеза не опровергнута, она в силе. Альтернативная гипотеза является обратной нулевой гипотезе.
Типы данных в статистике
Такие выражения, как минимум, максимум, медиана и процентиль имеют значение лишь для порядковых данных. Порядковые данные делятся на метрические и неметрические.
Что такое тренд?
Термины тренд и тенденция используются в различных целях. Люди часто говорят о тенденции относительно роста цен и падения курса какой-то валюты. Здесь мы раскроем статистическое значение этих терминов.
Ошибка репрезентативности
Стандартная ошибка (standard error) и ошибка репрезентативности часто употребляются, как взаимозаменяемые термины. Ошибка репрезентативности показывает, насколько результаты, полученные при выборочном наблюдении отличаются от результатов, полученных при исследовании генеральной совокупности.
Медиана в статистике
Медиана – середина упорядоченного ряда. Медиана делит этот ряд пополам таким образом, что в одной половине стоят все значения меньшие, а в другой все значения большие медианы.
© Все права защищены
Все статьи этого сайта написаны Джафаром Н.Алиевым. Перепечатывание любой статьи на стороннем ресурсе должно сопровождаться именем автора и ссылкой на данный ресурс. Сам автор следует этим правилам.
Статистика медиана мода среднее
Каков средний возраст современного кинозрителя? (величина А)
Какой самый популярный фильм 2016 года? (величина В)
Чему равен максимальный возраст младшей половины аудитории фильма «Кунг-фу Панда»? (величина С)
Такая информация всегда необходима кинокомпаниям, может быть полезна владельцам кинозалов и даже может заинтересовать кинозрителей. Знаете, что общего у этих разных, на первый взгляд, величин? Величины А, В и С являются серединами. О них мы и поговорим.
Начнём с того, что все эти величины – А, B и С – можно определить только тогда, если у вас есть данные. В первом случае, это количество людей, посетивших кинотеатры и их возраст. Во втором – список фильмов 2016 года и количество билетов, проданных на каждый фильм. И в последнем случае – это количество людей, посмотревших фильм «Кунг-фу Панда» с указанием их возраста.
Проанализировав и обработав имеющиеся данные, мы можем найти значение величин А, В и С. Каждая из названных величин является «центром» или «серединой» этих данных. В математической статистике их называют средним арифметическим (А), модой (В) и медианой (С). Эти величины несут в себе определённую информацию об имеющихся данных и могут быть полезными в повседневной жизни. Чтобы было понятно, объясним это на примере.
Средняя величина – это усреднённый показатель, который уничтожает индивидуальные различия и даёт обобщающую характеристику показателю. Бывают случаи, когда средняя арифметическая не совсем подходит для решения поставленной задачи и даже может ввести в заблуждение. Тогда используются другие средние величины – мода и медиана. Мода и медиана – важные показатели, они отражают структуру данных и, в отличие от средней арифметической, не погашают индивидуальных различий изучаемого показателя. Поэтому они являются дополнительными и очень важными характеристиками и на практике часто используются вместо средней арифметической либо наряду с ней.
Среди школьников четвёртых классов провели годовую контрольную по математике. Класс, который покажет наилучший результат, наградят поездкой в летний лагерь. В каждом классе по 30 учеников. Победителя решили определить, вычислив среднюю арифметическую оценку по каждому классу.
Самый распространённый вид средней величины – средняя арифметическая. Как она считается, знают все: нужно сложить все слагаемые и сумму разделить на количество этих слагаемых.
Результаты получились следующими:
Наивысший результат показал 4 «В» класс. «Ура! Мы едем в лагерь!» – обрадовались ученики 4 «В» класса. Но тут возмутились ученики 4 «А» и 4 «Б» классов: «Мы должны поехать в летний лагерь, у нас больше «пятёрок»! Директор был в замешательстве: «Что делать?»
Тогда учитель математики предложил посчитать моду.
Мода – это наиболее часто встречающееся значение в данных. Мода применяется, например, на обувных фабриках, при определении самого «ходового» размера обуви, то есть пользующегося наибольшим спросом у покупателей. В самом деле, не будут же производители обуви ориентироваться на средний размер обуви и шить всю обувь среднего размера.

Медиана – это некая отметка, делящая ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Она расположена в центре ранжированного ряда. То есть половина исходных данных по своему значению меньше этой отметки, а половина – больше.
Вот как нужно находить её в наборе данных.
«Ну теперь точно поедем мы!» – радовался 4 «А», наша медиана «4,5», а у 4 «Б» и 4 «В» – «четвёрка». Это значит, что половина нашего класса получила отметку выше, чем 4,5 (то есть только пятёрки), а у других классов эта же половина получила отметку выше «4» (то есть не только «пятёрки», но и «четвёрки»).
Но тут подал голос 4 «В», до этого не вступавший в спор: «А у нас вообще «троек» нет, значит, у нас нет отстающих, и это немаловажный показатель!». «А ведь они тоже правы», – подумал директор и ещё больше загрустил.
Итак, мы увидели, что, используя разные средние величины, мы получаем разные результаты, то есть каждый раз лучшим становится другой класс. Поэтому, чтобы выбрать самый лучший класс, надо сначала дать чёткое описание поставленной задачи, в зависимости от того, чего вы добиваетесь.
А какой класс отправили бы вы, будь вы на месте директора?
Среднее арифметическое, мода и медиана
Предмет, цели и методы математической статистики
Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.
Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
В зависимости от предмета исследований математическая статистика делится на:
В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.









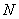 , а именно её числовая характеристика
, а именно её числовая характеристика 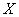 , не важно, дискретная или непрерывная (Занятия 2, 3).
, не важно, дискретная или непрерывная (Занятия 2, 3).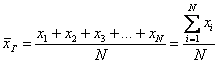
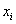 есть одинаковые (что характерно для дискретного ряда), то формулу можно записать в более компактном виде:
есть одинаковые (что характерно для дискретного ряда), то формулу можно записать в более компактном виде: 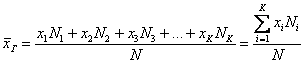 , где
, где 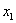 повторяется
повторяется 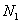 раз;
раз; 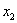 –
– 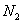 раз;
раз; 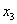 –
– 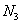 раз;
раз; 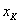 –
– 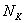 раз.
раз.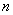 , и на основании исследования этой выборки делают вывод обо всей совокупности.
, и на основании исследования этой выборки делают вывод обо всей совокупности.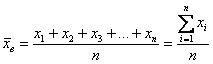
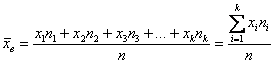 – как сумма произведений вариант
– как сумма произведений вариант 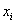 на соответствующие частоты
на соответствующие частоты 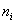 .
.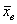 позволяет достаточно точно оценить истинное значение
позволяет достаточно точно оценить истинное значение 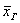 , чего вполне достаточно для многих исследований. При этом, чем больше выборка, тем точнее будет эта оценка.
, чего вполне достаточно для многих исследований. При этом, чем больше выборка, тем точнее будет эта оценка.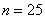 рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.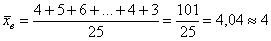 – среднестатистический квалификационный разряд рабочих цеха.
– среднестатистический квалификационный разряд рабочих цеха.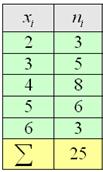
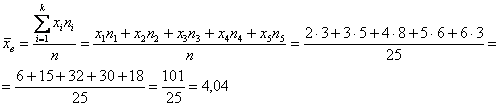
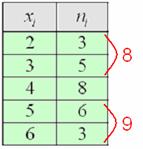
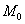 дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае
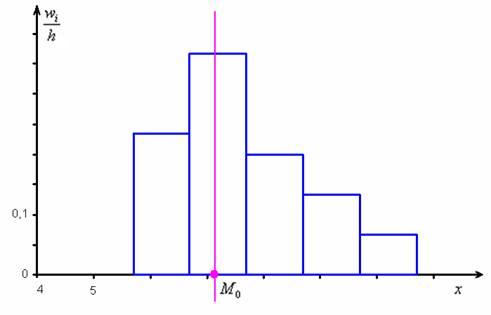
дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае 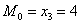 . Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки:
. Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки: 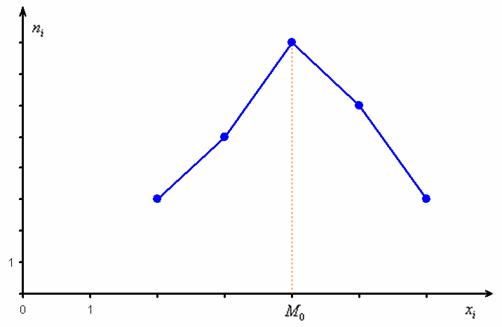
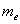 вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).
вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).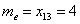 . Почему именно 13-е число? Потому что перед ним находится 12 чисел и после него тоже 12 чисел, таким образом, значение
. Почему именно 13-е число? Потому что перед ним находится 12 чисел и после него тоже 12 чисел, таким образом, значение 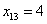 разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически:
разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически: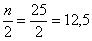 и округляем полученное значение в бОльшую сторону: 13 – получая тем самым срединный номер.
и округляем полученное значение в бОльшую сторону: 13 – получая тем самым срединный номер.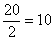 , и медианное значение здесь рассчитывается как среднее арифметическое 10-го и следующего числа:
, и медианное значение здесь рассчитывается как среднее арифметическое 10-го и следующего числа: 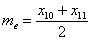 .
.
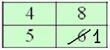
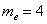
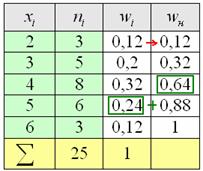
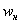 «переваливает» за отметку 0,5 (50% упорядоченной совокупности). Для 3-го разряда успело накопиться
«переваливает» за отметку 0,5 (50% упорядоченной совокупности). Для 3-го разряда успело накопиться 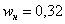 (32% совокупности), а вот для 4-го – уже
(32% совокупности), а вот для 4-го – уже 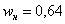 (64%). Таким образом, отметка в 50% пройдена именно здесь, и, стало быть,
(64%). Таким образом, отметка в 50% пройдена именно здесь, и, стало быть, 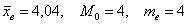
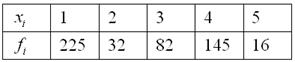
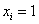 – количество пуговиц на пиджаке,
– количество пуговиц на пиджаке, 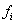 – число продаж, буква «эф» – это тоже достаточно популярная буква для обозначения частот, и она не должна вас смущать при встрече.
– число продаж, буква «эф» – это тоже достаточно популярная буква для обозначения частот, и она не должна вас смущать при встрече.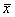 , без подстрочного индекса.
, без подстрочного индекса.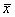 ? С такой статистикой магазин разорится.
? С такой статистикой магазин разорится.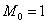 . Потому что такая мода 🙂 Более того, в прикладных исследованиях рассматривают несколько модальных значений (вроде даже в Экселе функция есть), в частности, ещё одной модой можно считать варианту
. Потому что такая мода 🙂 Более того, в прикладных исследованиях рассматривают несколько модальных значений (вроде даже в Экселе функция есть), в частности, ещё одной модой можно считать варианту 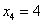 . Но это уже попсовая статистика, которую я не буду развивать в этом курсе.
. Но это уже попсовая статистика, которую я не буду развивать в этом курсе.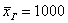 денежных единиц. Здесь мы плавно перешли к интервальному ряду, который целесообразно составлять для «денежных» показателей.
денежных единиц. Здесь мы плавно перешли к интервальному ряду, который целесообразно составлять для «денежных» показателей.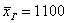 , и это уже будет несколько искажённая картина.
, и это уже будет несколько искажённая картина.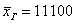 не только дезинформирует, но и вызовет широкое возмущение общественности.
не только дезинформирует, но и вызовет широкое возмущение общественности.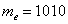 . Ниже этой планки зарабатывает ровно половина совокупности и выше – другая половина, включая Петрова и Петровского. …Главное только, чтобы они наняли правильного статистика 🙂
. Ниже этой планки зарабатывает ровно половина совокупности и выше – другая половина, включая Петрова и Петровского. …Главное только, чтобы они наняли правильного статистика 🙂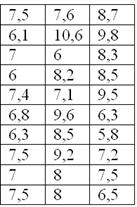
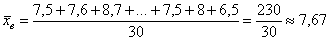 ден. ед.
ден. ед.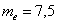 . Причём, здесь даже ничего не нужно сортировать.
. Причём, здесь даже ничего не нужно сортировать.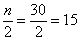 , и поскольку она состоит из чётного количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного ряда:
, и поскольку она состоит из чётного количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного ряда: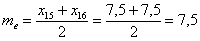 ден. ед.
ден. ед.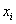 интервалов:
интервалов: 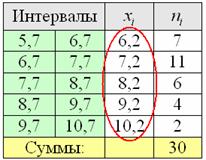
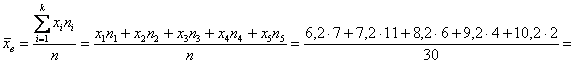
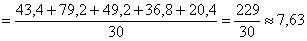 – отличный результат! Расхождение с более точным значением (
– отличный результат! Расхождение с более точным значением (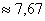 ), вычисленным по первичным данным, составляет всего 0,04.
), вычисленным по первичным данным, составляет всего 0,04.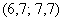 с частотой 11, и воспользоваться следующей страшненькой формулой:
с частотой 11, и воспользоваться следующей страшненькой формулой: 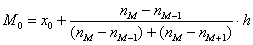 , где:
, где: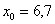 – нижняя граница модального интервала;
– нижняя граница модального интервала; 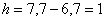 – длина модального интервала;
– длина модального интервала; 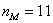 – частота модального интервала;
– частота модального интервала; 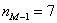 – частота предыдущего интервала;
– частота предыдущего интервала; 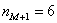 – частота следующего интервала.
– частота следующего интервала.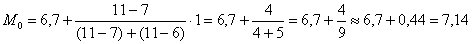 ден. ед. – как видите, «модная» цена на ботинки заметно отличается от средней арифметической
ден. ед. – как видите, «модная» цена на ботинки заметно отличается от средней арифметической 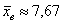 .
.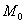 :
: 
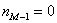 либо
либо 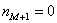 ;
;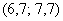 и
и 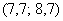 , то рассматриваем модальный интервал
, то рассматриваем модальный интервал 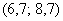 , при этом близлежащие интервалы (слева и справа) по возможности тоже укрупняем в 2 раза.
, при этом близлежащие интервалы (слева и справа) по возможности тоже укрупняем в 2 раза.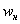 , здесь же сподручнее рассчитать «обычные» накопленные частоты
, здесь же сподручнее рассчитать «обычные» накопленные частоты 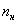 . Вычислительный алгоритм точно такой же – первое значение сносим слева (красная стрелка), и каждое следующее получается как сумма предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):
. Вычислительный алгоритм точно такой же – первое значение сносим слева (красная стрелка), и каждое следующее получается как сумма предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера): 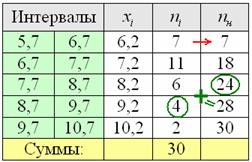
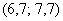 .
.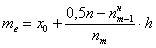 , где:
, где: 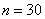 – объём статистической совокупности;
– объём статистической совокупности; 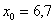 – нижняя граница медианного интервала;
– нижняя граница медианного интервала; 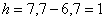 – длина медианного интервала;
– длина медианного интервала; 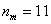 – частота медианного интервала;
– частота медианного интервала; 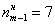 – накопленная частота предыдущего интервала.
– накопленная частота предыдущего интервала.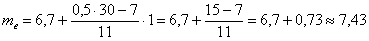 ден. ед. – заметим, что медианное значение, наоборот, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:
ден. ед. – заметим, что медианное значение, наоборот, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант: 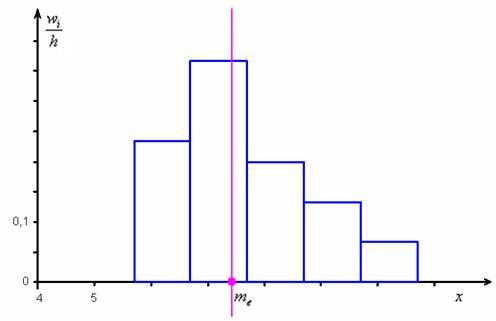
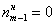 ;
;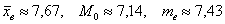 ден. ед.
ден. ед.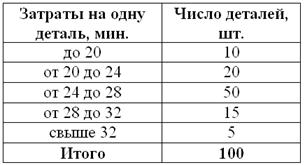
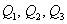 , которые делят его на 4 равные (по количеству вариант) части. Откуда автоматически следует, что 2-я квартиль – есть в точности медиана:
, которые делят его на 4 равные (по количеству вариант) части. Откуда автоматически следует, что 2-я квартиль – есть в точности медиана: 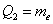 .
.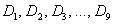 – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по количеству вариант) частей.
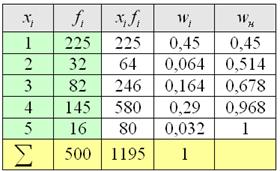
– это варианты, который делят упорядоченный вариационный ряд на 10 равных (по количеству вариант) частей. .
.
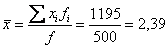 – две с половиной пуговицы, Карл!
– две с половиной пуговицы, Карл! 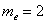 (именно здесь накопленная частота «перевалила» за 0,5).
(именно здесь накопленная частота «перевалила» за 0,5).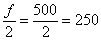 , а сумма первых двух частот
, а сумма первых двух частот 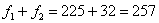 , то совершенно понятно, что 250-й и 251-й пиджак – двухпуговичные.
, то совершенно понятно, что 250-й и 251-й пиджак – двухпуговичные.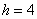 , то длины крайних интервалов полагаем такими же (см. конец статьи Интервальный вариационный ряд). Заполним расчётную таблицу:
, то длины крайних интервалов полагаем такими же (см. конец статьи Интервальный вариационный ряд). Заполним расчётную таблицу: 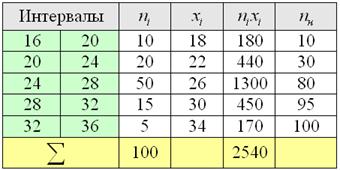
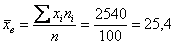 мин.
мин.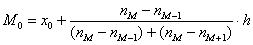 , в данном случае:
, в данном случае: 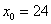 – нижняя граница модального интервала;
– нижняя граница модального интервала; 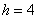 – длина модального интервала;
– длина модального интервала; 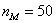 – частота модального интервала;
– частота модального интервала; 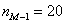 – частота предшествующего интервала;
– частота предшествующего интервала; 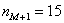 – частота следующего интервала.
– частота следующего интервала. 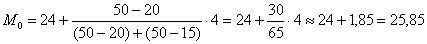 мин.
мин.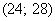 (именно он содержит 50-ю и 51-ю варианты, которые делят ряд пополам).
(именно он содержит 50-ю и 51-ю варианты, которые делят ряд пополам). 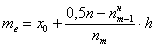 , в данном случае:
, в данном случае: 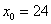 – нижняя граница медианного интервала;
– нижняя граница медианного интервала; 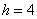 – длина этого интервала;
– длина этого интервала; 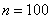 – объём статистической совокупности;
– объём статистической совокупности; 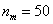 – частота медианного интервала;
– частота медианного интервала; 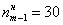 – накопленная частота предыдущего интервала.
– накопленная частота предыдущего интервала. 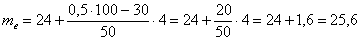 мин.
мин.
 «Всё сдал!» — онлайн-сервис помощи студентам
«Всё сдал!» — онлайн-сервис помощи студентам