средняя длина кода хаффмана
Алгоритм Хаффмана
Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.
Содержание
Определение [ править ]
Алгоритм построения бинарного кода Хаффмана [ править ]
Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:
Время работы [ править ]
Пример [ править ]
В дереве Хаффмана будет [math]5[/math] узлов:
| Узел | a | b | r | с | d |
|---|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 1 | 1 |
| Узел | a | b | r | cd |
|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 2 |
Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :
| Узел | a | rcd | b |
|---|---|---|---|
| Вес | 5 | 4 | 2 |
Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :
| Узел | brcd | a |
|---|---|---|
| Вес | 6 | 5 |
На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :
| Узел | abrcd |
|---|---|
| Вес | 11 |
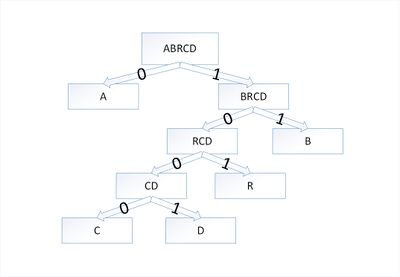
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):
| Символ | a | b | r | с | d |
|---|---|---|---|---|---|
| Код | 0 | 11 | 101 | 1000 | 1001 |
Корректность алгоритма Хаффмана [ править ]
Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.
[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_
из чего следует, что
[math] B(T) = B(T’) + f[x] + f[y] [/math]
Код Хаффмана
Построение кода Хаффмана для таблицы вероятностей.
Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.
Код Хаффмана
Таблица вероятности символов
Таблица вероятности символов
Импортировать данные Ошибка импорта
Небольшой отрывок из Википедии.
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.
Сжатие данных алгоритмом Хаффмана
Вступление
В данной статье я расскажу вам о широко известном алгоритме Хаффмана, и вы наконец разберетесь, как все там устроено изнутри. После прочтения вы сможете своими руками(а главное, головой) написать архиватор, сжимающий реальные, черт подери, данные! Кто знает, быть может именно вам светит стать следующим Ричардом Хендриксом!
Да-да, об этом уже была статья на Хабре, но без практической реализации. Здесь же мы сфокусируемся как на теоретической части, так и на программерской. Итак, все под кат!
Немного размышлений
В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASY\n». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — ‘\n’. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или ‘\n’) — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.
Кодирование
Почему бы символу ‘S’ не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ‘ ‘(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:
Ни один код не должен быть префиксом другого
Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:
Символы с наибольшим количеством вхождений должны кодироваться наименьшим возможным количеством битов. Приведу пример одной из возможных таблиц кодов:
Таким образом, закодированное сообщение будет выглядеть так:
Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос: как этот салага придумал код как создать таблицу кодов? Об этом пойдет речь ниже.
Построение дерева Хаффмана
Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:
Это не полный код, полный код будет ниже.
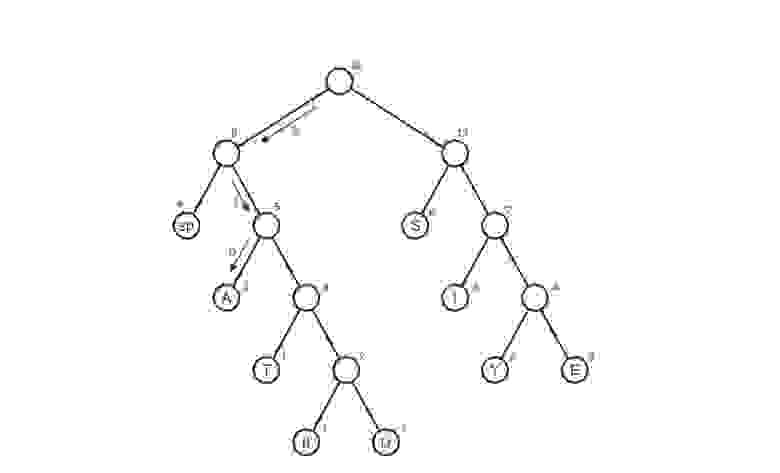
Вот сам алгоритм построения дерева:
Здесь символ «lf»(linefeed) обозначает переход на новую строку, «sp» (space) — это пробел.
А что дальше?
Мы получили дерево Хаффмана. Ну окей. И что с ним делать? Его и за бесплатно не возьмут А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.
Декодирование
Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:
Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:
Ни один код не должен являться префиксом другого
Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.
Реализация
Пришло время унижать мой код писать архиватор. Назовем его Compressor.
Начнем с начала. Первым делом пишем класс Node:
Класс, создающий дерево Хаффмана:
Класс, содержащий который кодирует/декодирует:
Класс, облегчающий запись в файл:
Класс, облегчающий чтение из файла:
Ну, и главный класс:
Файл с инструкциями readme.txt предстоит вам написать самим 🙂
Заключение
Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу моей некомпетентности улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!
Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то только не по лицу вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.
Выпустил upgrade: добавил GUI + изменил алгоритм обработки исходного текста так, чтобы не читать весь файл в память. Короче, кидаю ссылку на git для любознательных: сами всё увидите.
Благодарности
Как и автор каждой хорошей книги, я созидал эту статью не без помощи других людей. Имхо, очень мало людей сделало что-то крутое в одиночку.
Огромное спасибо Исаеву Виталию Вячеславовичу за небходимую теоретическую поддержку.
Также, часть материала этой статьи взята из книги Роберта Лафоре «Data Structures and Algorithms in Java». Если сомневаетесь как или окуда начать свой путь в теории алгоритмов и структур данных — берите, не прогадаете.
Алгоритмы сжатия данных
Кодовые деревья
Рассмотрим реализацию алгоритма Хаффмана с использованием кодовых деревьев.
Метод Хаффмана на входе получает таблицу частот встречаемости символов в исходном тексте. Далее на основании этой таблицы строится дерево кодирования Хаффмана.
Алгоритм построения дерева Хаффмана.
Шаг 2. Выбираются два свободных узла дерева с наименьшими весами.
Шаг 3. Создается их родитель с весом, равным их суммарному весу.
Шаг 4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.
Существует два подхода к построению кодового дерева: от корня к листьям и от листьев к корню.
Пример построения кодового дерева. Пусть задана исходная последовательность символов:
Ее исходный объем равен 20 байт (160 бит ). В соответствии с приведенными на рис. 41.1 данными ( таблица вероятности появления символов, кодовое дерево и таблица оптимальных префиксных кодов ) закодированная исходная последовательность символов будет выглядеть следующим образом:
Следовательно, ее объем будет равен 42 бита. Коэффициент сжатия приближенно равен 3,8.
Классический алгоритм Хаффмана имеет один существенный недостаток. Для восстановления содержимого сжатого текста при декодировании необходимо знать таблицу частот, которую использовали при кодировании. Следовательно, длина сжатого текста увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию данных. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по тексту: одного для построения модели текста (таблицы частот и дерева Хаффмана), другого для собственно кодирования.
Пример 2. Программная реализация алгоритма Хаффмана с помощью кодового дерева.
Ключевые термины
Сжатие данных – это процесс, обеспечивающий уменьшение объема данных путем сокращения их избыточности.
Сжатие без потерь (полностью обратимое) – это метод сжатия данных, при котором ранее закодированная порция данных восстанавливается после их распаковки полностью без внесения изменений.
Сжатие с потерями – это метод сжатия данных, при котором для обеспечения максимальной степени сжатия исходного массива данных часть содержащихся в нем данных отбрасывается.
Алфавит кода – это множество всех символов входного потока.
Кодовый символ – это наименьшая единица данных, подлежащая сжатию.
Кодовое слово – это последовательность кодовых символов из алфавита кода.
Токен – это единица данных, записываемая в сжатый поток некоторым алгоритмом сжатия.
Фраза – это фрагмент данных, помещаемый в словарь для дальнейшего использования в сжатии.
Кодирование – это процесс сжатия данных.
Декодирование – это обратный кодированию процесс, при котором осуществляется восстановление данных.
Отношение сжатия – это величина для обозначения эффективности метода сжатия, равная отношению размера выходного потока к размеру входного потока.
Коэффициент сжатия – это величина, обратная отношению сжатия.
Средняя длина кодового слова – это величина, которая вычисляется как взвешенная вероятностями сумма длин всех кодовых слов.
Статистические методы – это методы сжатия, присваивающие коды переменной длины символам входного потока, причем более короткие коды присваиваются символам или группам символам, имеющим большую вероятность появления во входном потоке.
Словарное сжатие – это методы сжатия, хранящие фрагменты данных в некоторой структуре данных, называемой словарем.
Хаффмановское кодирование (сжатие) – это метод сжатия, присваивающий символам алфавита коды переменной длины основываясь на вероятностях появления этих символов.
Префиксный код – это код, в котором никакое кодовое слово не является префиксом любого другого кодового слова.
Средняя длина кода хаффмана
Кодирование Хаффмана является простым алгоритмом для построения кодов переменной длины, имеющих минимальную среднюю длину. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Метод Хаффмана [Huffman 52] производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Алгоритм начинает строить кодовое дерево снизу вверх, затем скользит вниз по дереву, чтобы построить каждый индивидуальный код справа налево (от самого младшего бита к самому старшему). Начиная с работ Д.Хаффмана 1952 года, этот алгоритм являлся предметом многих исследований. (Последнее утверждение из § 3.8.1 показывает, что наилучший код переменной длины можно иногда получить без этого алгоритма.)
Алгоритм начинается составлением списка символов алфавита в порядке убывания их вероятностей. Затем от корня строится дерево, листьями которого служат эти символы. Это делается по шагам, причем на каждом шаге выбираются два символа с наименьшими вероятностями, добавляются наверх частичного дерева, удаляются из списка и заменяются вспомогательным символом, представляющим эти два символа. Вспомогательному символу приписывается вероятность, равная сумме вероятностей, выбранных на этом шаге символов. Когда список сокращается до одного вспомогательного символа, представляющего весь алфавит, дерево объявляется построенным. Завершается алгоритм спуском по дереву и построением кодов всех символов.
Лучше всего проиллюстрировать этот алгоритм на простом примере. Имеется пять символов с вероятностями, заданными на рис. 1.3а.
Рис. 1.3. Коды Хаффмана.
Символы объединяются в пары в следующем порядке:
1. 
объединяется с 
, и оба заменяются комбинированным символом 
с вероятностью 0.2;
2. Осталось четыре символа, 
с вероятностью 0.4, а также 
и с вероятностями по 0.2. Произвольно выбираем 
и , объединяем их и заменяем вспомогательным символом 
с вероятностью 0.4;
3. Теперь имеется три символа 
и с вероятностями 0.4, 0.2 и 0.4, соответственно. Выбираем и объединяем символы 
и во вспомогательный символ 
с вероятностью 0.6;
4. Наконец, объединяем два оставшихся символа и и заменяем на 
с вероятностью 1.
Средняя длина этого кода равна 
бит/символ. Очень важно то, что кодов Хаффмана бывает много. Некоторые шаги алгоритма выбирались произвольным образом, поскольку было больше символов с минимальной вероятностью. На рис. 1.3b показано, как можно объединить символы по-другому и получить иной код Хаффмана (11, 01, 00, 101 и 100). Средняя длина равна 
бит/символ как и у предыдущего кода.
Пример: Дано 8 символов А, В, С, D, Е, F, G и H с вероятностями 1/30, 1/30, 1/30, 2/30, 3/30, 5/30, 5/30 и 12/30. На рис. 1.4а,b,с изображены три дерева кодов Хаффмана высоты 5 и 6 для этого алфавита.
Рис. 1.4. Три дерева Хаффмана для восьми символов.
Средняя длина этих кодов (в битах на символ) равна
,
,
.
Пример: На рис. 1.4d показано другое дерево высоты 4 для восьми символов из предыдущего примера. Следующий анализ показывает, что соответствующий ему код переменной длины плохой, хотя его длина меньше 4.
(Анализ.) После объединения символов А, В, С, D, Е, F и G остаются символы ABEF (с вероятностью 10/30), CDG (с вероятностью 8/30) и H (с вероятностью 12/30). Символы ABEF и CDG имеют наименьшую вероятность, поэтому их необходимо было слить в один, но вместо этого были объединены символы CDG и H. Полученное дерево не является деревом Хаффмана.
Таким образом, некоторый произвол в построении дерева позволяет получать разные коды Хаффмана с одинаковой средней длиной. Напрашивается вопрос: «Какой код Хаффмана, построенный для данного алфавита, является наилучшим?» Ответ будет простым, хотя и неочевидным: лучшим будет код с наименьшей дисперсией.
Дисперсия показывает насколько сильно отклоняются длины индивидуальных кодов от их средней величины (это понятие разъясняется в любом учебнике по статистике). Дисперсия кода 1.3а равна 
, а для кода 1.3b 
.
Код 1.3b является более предпочтительным (это будет объяснено ниже). Внимательный взгляд на деревья показывает, как выбрать одно, нужное нам. На дереве рис. 1.3а символ сливается с символом , в то время как на рис. 1.3b он сливается с . Правило будет такое: когда на дереве имеется более двух узлов с наименьшей вероятностью, следует объединять символы с наибольшей и наименьшей вероятностью; это сокращает общую дисперсию кода.
Если кодер просто записывает сжатый файл на диск, то дисперсия кода не имеет значения. Коды Хаффмана с малой дисперсией более предпочтительны только в случае, если кодер будет передавать этот сжатый файл по линиям связи. В этом случае, код с большой дисперсией заставляет кодер генерировать биты с переменной скоростью. Обычно данные передаются по каналам связи с постоянной скоростью, поэтому кодер будет использовать буфер. Биты сжатого файла помещаются в буфер по мере их генерации и подаются в канал с постоянной скоростью для передачи. Легко видеть, что код с нулевой дисперсией будет подаваться в буфер с постоянной скоростью, поэтому понадобится короткий буфер, а большая дисперсия кода потребует использование длинного буфера.
Следующее утверждение можно иногда найти в литературе по сжатию информации: длина кода Хаффмана символа 
с вероятностью 
всегда не превосходит 
. На самом деле, не смотря на справедливость этого утверждения во многих примерах, в общем случае оно не верно. Я весьма признателен Гаю Блелоку, который указал мне на это обстоятельство и сообщил пример кода, приведенного в табл. 1.5. Во второй строке этой таблицы стоит символ с кодом длины 3 бита, в то время как 
.
является степенью 2, то получаются просто коды фиксированной длины. В других случаях коды весьма близки к кодам с фиксированной длиной. Это означает, что использование кодов переменной длины не дает никаких преимуществ. В табл. 1.8 приведены коды, их средние длины и дисперсии.
, в которой каждый символ встречается длинными сериями. Такую строку можно сжать методом RLE, но не методом Хаффмана. (Буквосочетание RLE означает «run-length encoding», т.е. «кодирование длин серий». Этот простой метод сам по себе мало эффективен, но его можно использовать в алгоритмах сжатия со многими этапами, см. [Salomon, 2000).)
увеличивается до длины 
, то число групп растет экспоненциально с 
до 
).
, выбирается одно семейство кодов, и