сортировка пузырьком питон код
Сортировка методом пузырька в Python
На сегодняшний день создано множество алгоритмов сортировки, каждый из которых решает весьма распространенную задачу — сортировку данных.
Сортировка пузырьком — это один из самых простых, но и малоэффективных алгоритмов, который используется для сортировки небольших массивов.
Алгоритмы сортировки на собеседовании
Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.
На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.
На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:
Метод пузырька
Сортировка пузырьком в основном применяется в учебных проектах. В реальной практике её заменяют более эффективные алгоритмы, однако сортировка пузырьком лежит в основе некоторых из них.
В общем случае алгоритм сортировки пузырьком следующий:
В алгоритме используется два цикла: основной и вложенный. В результате одного прохода вложенного цикла наибольший элемент помещается в конец массива, а наименьший смещается на одну позицию ближе к началу.
Внешний цикл в худшем случае совершает N (кол-во элементов) — 1 проходов, то есть внутренний цикл выполняется N-1 раз.
Таким образом, в каждом проходе совершается серия обменов элементов так, что наибольший элемент передвигается в конец массив перед элементом, который переместился туда в прошлой итерации. Процесс происходит до тех пор, пока массив не будет отсортирован.
Сложность алгоритма
Сложность алгоритма позволяет дать ему оценку по времени выполнения, то есть определяет его эффективность. Можно выражать сложность по-разному, но чаще всего используется асимптотическая сложность, которая определяет его эффективность при стремлении входных данных к бесконечности.
Точное время выполнения алгоритма не рассматривается, потому что оно зависит слишком от многих факторов: мощность процессора, тип данных массива, используемый язык программирования.
Следует понимать, что с помощью асимптотической функции нельзя точно вычислить время работы алгоритма. Например, дана последовательность «6 5 4 3 2 1», для её сортировки придется сделать максимальное количество проходов. Такой случай называют наихудшим. Если дана последовательность «3 1 2 4 5», то количество проходов будет минимально, соответственно сортировка пройдет гораздо быстрее. Если же дан уже отсортированный массив, то алгоритму сортировки и вовсе не нужно совершать проходов. Это называется наилучшим случаем.
Реализация на Python
Сортировку пузырьком лучше вывести в отдельную функцию. Код функции будет выглядеть так:
Реализовать обмен значений соседних элементов можно в одну строку, использовав множественное присваивание, тогда код будет выглядеть так:
Множественное присваивание — одна из полезных фич Python, позволяющее не вводить дополнительную переменную для обмена значений двух и более переменных.
Чтобы продемонстрировать работу функции пузырьковой сортировки, создадим список, которые необходимо отсортировать:
Отсортируем его с помощью нашей функции и выведем на экран:
Заключение
Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.
Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.
Сортировка пузырьком
В процессе выполнения данного алгоритма элементы с большими значениями оказываются в конце списка, а элементы с меньшими значениями постепенно перемещаются по направлению к началу списка. Образно говоря, тяжелые элементы падают на дно, а легкие медленно всплывают подобно пузырькам воздуха.
В сортировке методом пузырька количество итераций внешнего цикла определяется длинной списка минус единица, так как когда второй элемент становится на свое место, то первый уже однозначно минимальный и находится на своем месте.
Количество итераций внутреннего цикла зависит от номера итерации внешнего цикла, так как конец списка уже отсортирован, и выполнять проход по этим элементам смысла нет.
Пусть имеется список [6, 12, 4, 3, 8].
За первую итерацию внешнего цикла число 12 переместится в конец. Для этого потребуется 4 сравнения во внутреннем цикле:
Результат: [6, 4, 3, 8, 12]
За вторую итерацию внешнего цикла число 8 переместиться на предпоследнее место. Для этого потребуется 3 сравнения:
Результат: [4, 3, 6, 8, 12]
На третьей итерации внешнего цикла исключаются два последних элемента. Количество итераций внутреннего цикла равно двум:
Результат: [3, 4, 6, 8, 12]
На четвертой итерации внешнего цикла осталось сравнить только первые два элемента, поэтому количество итераций внутреннего равно единице:
Результат: [3, 4, 6, 8, 12]
Реализация сортировки пузырьком с помощью циклов for
Пример выполнения кода:
С помощью циклов while
Функция сортировки пузырьком на Python
Объяснение алгоритмов сортировки с примерами на Python
В этой статье будут рассмотрены популярные алгоритмы, принципы их работы и реализация на Python. А ещё сравним, как быстро они сортируют элементы в списке.
В качестве общего примера возьмём сортировку чисел в порядке возрастания. Но эти методы можно легко адаптировать под ваши потребности.
Пузырьковая сортировка
Этот простой алгоритм выполняет итерации по списку, сравнивая элементы попарно и меняя их местами, пока более крупные элементы не «всплывут» в начало списка, а более мелкие не останутся на «дне».
Алгоритм
Сначала сравниваются первые два элемента списка. Если первый элемент больше, они меняются местами. Если они уже в нужном порядке, оставляем их как есть. Затем переходим к следующей паре элементов, сравниваем их значения и меняем местами при необходимости. Этот процесс продолжается до последней пары элементов в списке.
При достижении конца списка процесс повторяется заново для каждого элемента. Это крайне неэффективно, если в массиве нужно сделать, например, только один обмен. Алгоритм повторяется n² раз, даже если список уже отсортирован.
13 сентября – 9 октября, Санкт-Петербург и онлайн, Беcплатно
Для оптимизации алгоритма нужно знать, когда его остановить, то есть когда список отсортирован.
Реализация
Время сортировки
Если взять самый худший случай (изначально список отсортирован по убыванию), затраты времени будут равны O(n²), где n — количество элементов списка.
Сортировка выборкой
Этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Наименьший элемент удаляется из второго списка и добавляется в первый.
Алгоритм
На практике не нужно создавать новый список для отсортированных элементов. В качестве него используется крайняя левая часть списка. Находится наименьший элемент и меняется с первым местами.
Теперь, когда нам известно, что первый элемент списка отсортирован, находим наименьший элемент из оставшихся и меняем местами со вторым. Повторяем это до тех пор, пока не останется последний элемент в списке.
Реализация
По мере увеличения значения i нужно проверять меньше элементов.
Время сортировки
Затраты времени на сортировку выборкой в среднем составляют O(n²), где n — количество элементов списка.
Сортировка вставками
Как и сортировка выборкой, этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Алгоритм перебирает второй сегмент и вставляет текущий элемент в правильную позицию первого сегмента.
Алгоритм
Переходя к другим элементам несортированного сегмента, перемещаем более крупные элементы в отсортированном сегменте вверх по списку, пока не встретим элемент меньше x или не дойдём до конца списка. В первом случае x помещается на правильную позицию.
Реализация
Время сортировки
Время сортировки вставками в среднем равно O(n²), где n — количество элементов списка.
Пирамидальная сортировка
Также известна как сортировка кучей. Этот популярный алгоритм, как и сортировки вставками или выборкой, сегментирует список на две части: отсортированную и неотсортированную. Алгоритм преобразует второй сегмент списка в структуру данных «куча» (heap), чтобы можно было эффективно определить самый большой элемент.
Алгоритм
Сначала преобразуем список в Max Heap — бинарное дерево, где самый большой элемент является вершиной дерева. Затем помещаем этот элемент в конец списка. После перестраиваем Max Heap и снова помещаем новый наибольший элемент уже перед последним элементом в списке.
Этот процесс построения кучи повторяется, пока все вершины дерева не будут удалены.
Реализация
Создадим вспомогательную функцию heapify() для реализации этого алгоритма:
Время сортировки
В среднем время сортировки кучей составляет O(n log n), что уже значительно быстрее предыдущих алгоритмов.
Сортировка слиянием
Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.
Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.
Алгоритм
Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.
Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.
Реализация
Время сортировки
В среднем время сортировки слиянием составляет O(n log n).
Быстрая сортировка
Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие — позади.
Алгоритм
Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.
Реализация
Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).
Время выполнения
В среднем время выполнения быстрой сортировки составляет O(n log n).
Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²).
Встроенные функции сортировки на Python
Иногда полезно знать перечисленные выше алгоритмы, но в большинстве случаев разработчик, скорее всего, будет использовать функции сортировки, уже предоставленные в языке программирования.
Отсортировать содержимое списка можно с помощью стандартного метода sort() :
Или можно использовать функцию sorted() для создания нового отсортированного списка, оставив входной список нетронутым:
Оба эти метода сортируют в порядке возрастания, но можно изменить порядок, установив для флага reverse значение True :
В отличие от других алгоритмов, обе функции в Python могут сортировать также списки кортежей и классов. Функция sorted() может сортировать любую последовательность, которая включает списки, строки, кортежи, словари, наборы и пользовательские итераторы, которые вы можете создать.
Функции в Python реализуют алгоритм Tim Sort, основанный на сортировке слиянием и сортировке вставкой.
Сравнение скоростей сортировок
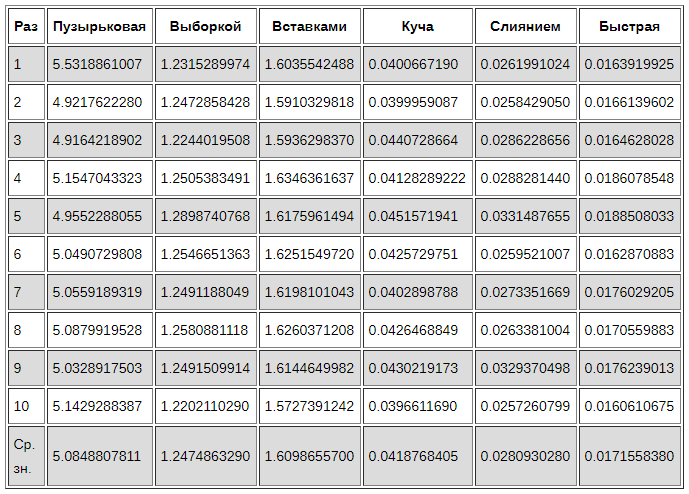
Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.
Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.
Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.
Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.
Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.
Лучше понять эти алгоритмы вам поможет их визуализация.
Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.
Перейти к регистрации
Пузырьковая сортировка в Python
Сортировка пузырьком – это простой алгоритм среди различных алгоритмов сортировки. Изучим его как первый алгоритм сортировки. Его легко освоить и он интуитивно очень понятен. Его несложно реализовать в коде, что очень выгодно для начинающих разработчиков программного обеспечения. Минус алгоритма в том, что для сортировки элементов данный метод производит проверку каждый раз, независимо от того, сортируется массив или нет.
Концепция пузырьковой сортировки
Разберемся на примере.
Мы создаем список элементов, в котором хранятся целые числа
list1 = [5, 3, 8, 6, 7, 2]
Так алгоритм сортирует элементы:
Первая итерация
Он сравнивает первые два элемента, и здесь 5> 3, а затем меняет их местами. Теперь у нас есть новый список –
Во втором сравнении 5 6, элементы меняются местами –
В четвертом сравнении 8> 7, элементы меняются местами –
В пятом сравнении 8> 2, также нужно их поменять местами –
На этом первая итерация завершена, и в конце мы получаем самый большой элемент. Теперь нам нужно len (list1) – 1
Вторая итерация
Пятая итерация
Мы видим, что наш список отсортирован с использованием метода пузырьковой сортировки.
Реализация в коде Python
Мы уже описывали технику пузырьковой сортировки. Теперь реализуем логику в коде Python.
В приведенном выше коде мы определили функцию bubble_sort(), которая принимает list1 в качестве аргумента.
Без использования временной переменной
Мы также можем поменять местами элементы, не используя временную переменную. У Python очень уникальный синтаксис. Мы можем использовать следующие строки кода.
Оптимизация реализации кода Python
Мы можем оптимизировать приведенный выше код, используя два метода. Свопы не производятся; это означает, что список отсортирован. В предыдущем методе оценивается полный список, хотя в этом нет необходимости.
Мы можем предотвратить ненужную оценку, используя логический флаг и проверяя, были ли сделаны какие-либо свопы в предыдущем разделе.
Во втором методе мы учитываем тот факт, что итерация заканчивается, когда самый большой элемент списка оказывается в конце списка.
В первый раз мы передаем самый большой элемент в конечную позицию, используя позицию n. Во второй раз мы проходим через позицию n-1, второй по величине элемент.
На каждой последующей итерации мы можем сравнивать на один элемент меньше, чем раньше. Точнее, на k-й итерации нужно сравнить только первые n – k + 1 элементов:
Сравнение времени
Давайте посмотрим на сравнение времени между приведенными выше фрагментами кода.
Все методы применимы для небольшого числа элементов, но если список состоит из многих элементов, то второй метод оптимизации имеет огромное значение.
Пузырьковая сортировка на Python и С#
В этом материале мы поговорим про алгоритм сортировки пузырьком (Bubble sort). Для примера попробуем отсортировать массив вручную, после чего напишем код для сортировки пузырьком на языке программирования Python и Си шарп.
Описание алгоритма
В процессе сортировки пузырьком происходит попарное сравнение соседних элементов массива, начиная с нулевого. После первой итерации самое большое число окажется на месте последнего, причем в дальнейших итерациях это значение уже задействоваться не будет (по сути, мы получим n-1 сравнений). Далее алгоритм находит второй по величине элемент, который ставится на предпоследнее место, потом третий и пр. В результате на месте нулевого элемента (не забываем, что нумерация в массиве начинается с нуля) окажется наименьшее число, а на месте последнего элемента – наибольшее. То есть мы можем сказать, что элементы от большего к меньшему «всплывают» по аналогии с пузырьками.
Проговорим алгоритм еще раз:
Важно понимать, что при реализации сортировки применяют 2 цикла: основной и вложенный (внутренний цикл). По результатам одного прохода внутреннего цикла самый большой элемент смещается в конец массива, тогда как самый маленький перемещается к началу (на одну позицию).
Рассмотрим пример
Представьте, что у нас есть следующий массив:
В процессе первой итерации мы возьмем нулевой элемент (это 7) и сравним его с соседним. Так как семь больше двух, числа меняются своими местами. То есть массив меняется:
2 7 9 4 1 0
Потом происходит сравнение второго и третьего числа. Так как изначально 9 больше семи, то семь остается на месте. Далее 9 последовательно сравнивается с остальными значениями и таким образом постепенно перемещается в самый конец массива (так как числа, большего, чем 9, в массиве нет, девятка занимает заслуженное последнее место).
2 7 4 1 0 9
Первая итерация закончена, количество шагов уменьшилось на 1 (n-1), то есть 9 находится там, где надо. Больше это число не затрагивается.
Во второй итерации все опять начинается с нулевого элемента массива (в нашем случае это двойка) с последующими сравнениями и перемещениями. В результате массив будет выглядеть следующим образом:
2 4 1 0 7 9
И так далее. Итоговый вид массива после сортировки по методу пузырьком вы можете видеть ниже:
Как видите, ничего сложного в этом нет.
Реализация на Си шарп
Чтобы реализовать сортировку пузырьком, сначала над создать саму функцию сортировки, которая будет располагаться в итоге перед функцией main: