обратный код двоичного числа калькулятор
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Обратный код двоичного числа калькулятор
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код 
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Двоично-десятичное кодирование
Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот.
После калькулятора Перевод дробных чисел из одной системы счисления в другую я думал, что тема с системами счисления уже закрыта. Но, как оказалось, еще нет.
Как я писал по ссылке выше, основная проблема при переводе дробных чисел из одной системы счисления в другую это потеря точности, когда, например, десятичное число 0.8 нельзя перевести в двоичное без погрешности.
Поскольку десятичные числа активно используются человеком, а двоичные — компьютером, этой проблемой в применении к двоичной и десятичной системам однажды уже озаботились какие-то светлые умы и придумали двоично-десятичное кодирование (binary coded decimal, BCD). Суть идеи проста — берем и для каждой десятичной цифры заводим байт. И в этом байте тупо пишем значение десятичной цифры в двоичном коде. Тогда число, например, 0.8 будет 0.00001000. Потом, правда, подумали еще, и решили, что раз уж верхняя часть байта всегда пустует (так как максимум 9 — это 1001), то давайте для каждой десятичной цифры заводить полубайт. И назвали это упакованным двоично-десятичным кодированием (packed BCD).
В упакованном кодировании наше 0.8 будет 0.1000, а какое-нибудь 6.75 будет 0110.01110101.
Прекрасная идея, конечно. Точность не теряется, человек может двоичные числа переводить в десятичные и наоборот прямо на лету, округлять можно, откидывая лишнее. Но как-то не получила она широкого распространения, потому как жизнь машинам она, наоборот, усложняла — и памяти для хранения чисел надо больше, и операции над числами реализовать сложнее. Так и осталась забавным курьезом, и я бы ничего о ней не знал, если бы пользователи не подсказали, что есть такая.
Ну и небольшой калькулятор по этому поводу — вводим либо десятичное число, либо двоичное, подразумевая, что это упакованный двоично-десятичный код, и получаем результат. Понятно, что все преобразования можно проделать и в уме, и в этом ее преимущество; но зачем же лишний раз мозги напрягать, верно?
Представление чисел в ЭВМ
Целые числа
Для числа +1101 :
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
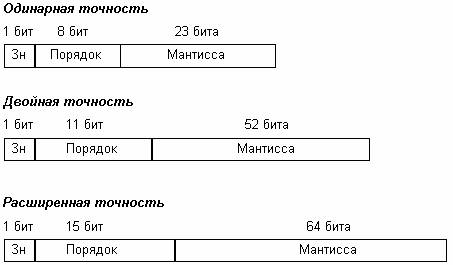
Вещественные числа (числа с плавающей точкой)
0.15625 = 001012
446.15625 = 110111110,001012 = 1,1011111000101*2 8
Знак S = 0
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE2800000000016
455,375 = 111000111,01102 = 1,110001110110*2 8 2
Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 100000010002 = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101
1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881
б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 100000010002 = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011
1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818