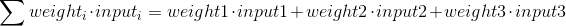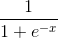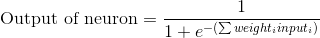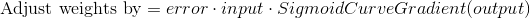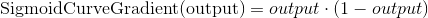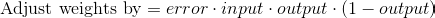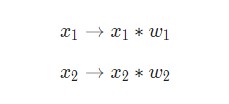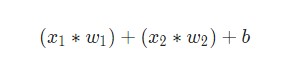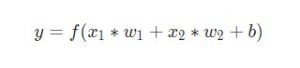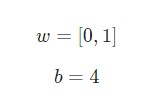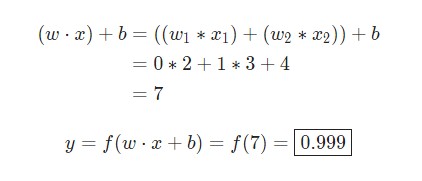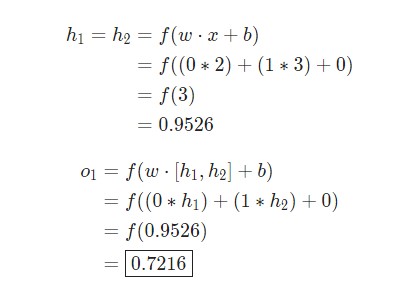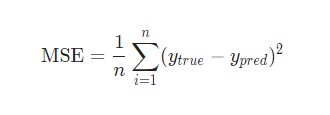нейросеть на питоне код
Простая нейронная сеть в 9 строк кода на Python
Из статьи вы узнаете, как написать свою простую нейросеть на python с нуля, не используя никаких библиотек для нейросетей. Если у вас еще нет своей нейронной сети, вот всего лишь 9 строчек кода:
Перед вами перевод поста How to build a simple neural network in 9 lines of Python code, автор — Мило Спенсер-Харпер. Ссылка на оригинал — в подвале статьи.
В статье мы разберем, как это получилось, и вы сможете создать свою собственную нейронную сеть на python. Также будут показаны более длинные и красивые версии кода.

Но для начала, что же такое нейронная сеть? Человеческий мозг состоит из 100 миллиарда клеток, называемых нейронами, соединенных синапсами. Если достаточное количество синаптичеких входов возбуждены, то и нейрон тоже становится возбужденным. Этот процесс также называется “мышление”.
Мы можем смоделировать этот процесс, создав нейронную сеть на компьютере. Не обязательно моделировать всю сложную модель человеческого мозга на молекулярном уровне, достаточно только высших правил мышления. Мы используем математические техники называемые матрицами, то есть просто сетки с числами. Чтобы сделать все максимально просто, построим модель из трех входных сигналов и одного выходного.
Мы будем тренировать нейрон на решение задачи, представленной ниже.
Первые четыре примера назовем тренировочной выборкой. Вы сможете выделить закономерность? Что должно стоять на месте “?”
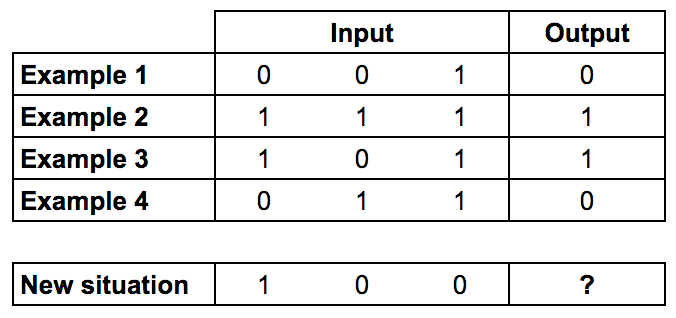
Вероятно вы заметили, что выходной сигнал всегда равен самой левой входной колонке. Таким образом ответ будет 1.
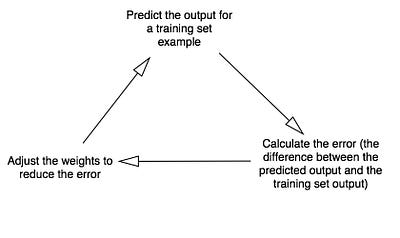
Процесс обучения нейронной сети
Как же должно происходить обучение нашего нейрона, чтобы он смог ответить правильно? Мы добавим каждому входу вес, который может быть положительным или отрицательным числом. Вход с большим положительным или большим отрицательным весом сильно повлияет на выход нейрона. Прежде чем мы начнем, установим каждый вес случайным числом. Затем начнем обучение:
В конце концов вес нейрона достигнет оптимального значения для тренировочного набора. Если мы позволим нейрону «подумать» в новой ситуации, которая сходна с той, что была в обучении, он должен сделать хороший прогноз.
Формула для расчета выхода нейрона
Вам может быть интересно, какова специальная формула для расчета выхода нейрона? Сначала мы берем взвешенную сумму входов нейрона, которая:
Затем мы нормализуем это, поэтому результат будет между 0 и 1. Для этого мы используем математически удобную функцию, называемую функцией Sigmoid:
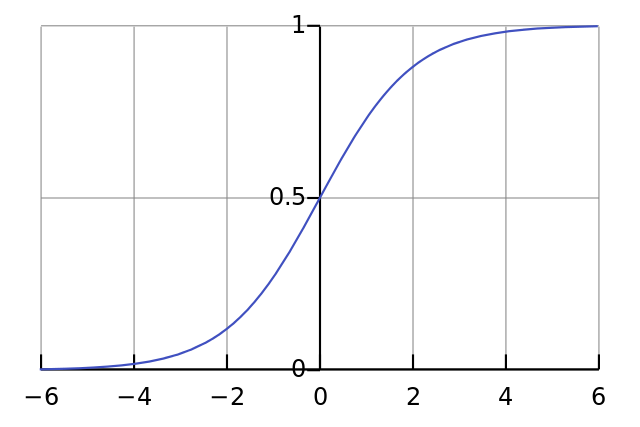
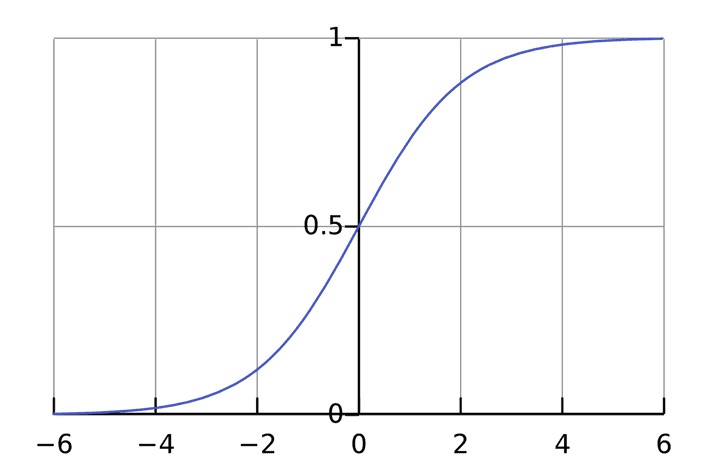
Если график нанесен на график, функция Sigmoid рисует S-образную кривую.
Подставляя первое уравнение во второе, получим окончательную формулу для выхода нейрона:
Возможно, вы заметили, что мы не используем пороговый потенциал для простоты.
Формула для корректировки веса
Во время тренировочного цикла (Диаграмма 3) мы корректируем веса. Но насколько мы корректируем вес? Мы можем использовать формулу «Взвешенная по ошибке» формула
Почему эта формула? Во-первых, мы хотим сделать корректировку пропорционально величине ошибки. Во-вторых, мы умножаем на входное значение, которое равно 0 или 1. Если входное значение равно 0, вес не корректируется. Наконец, мы умножаем на градиент сигмовидной кривой (диаграмма 4). Чтобы понять последнее, примите во внимание, что:
Градиент Сигмоды получается, если посчитать взятием производной:
Вычитая второе уравнение из первого получаем итоговую формулу:
Существуют также другие формулы, которые позволяют нейрону учиться быстрее, но приведенная имеет значительное преимущество: она простая.
Написание Python кода
Хоть мы и не будем использовать библиотеки с нейронными сетями, мы импортируем 4 метода из математической библиотеки numpy. А именно:
Например, мы можем использовать array() для представления обучающего множества, показанного ранее.
“.T” — функция транспонирования матриц. Итак, теперь мы готовы для более красивой версии исходного кода. Заметьте, что на каждой итерации мы обрабатываем всю тренировочную выборку одновременно.
Код также доступен на гитхабе. Если вы используете Python3 нужно заменить xrange на range.
Заключительные мысли
Попробуйте запустить нейросеть, используя команду терминала:
Итоговый должен быть похож на это:
У нас получилось! Мы написали простую нейронную сеть на Python!
Сначала нейронная сеть присваивала себе случайные веса, а затем обучалась с использованием тренировочного набора. Затем нейросеть рассмотрела новую ситуацию [1, 0, 0] и предсказала 0.99993704. Правильный ответ был 1. Так очень близко!
Традиционные компьютерные программы обычно не могут учиться. Что удивительного в нейронных сетях, так это то, что они могут учиться, адаптироваться и реагировать на новые ситуации. Так же, как человеческий разум.
Конечно, это был только 1 нейрон, выполняющий очень простую задачу. А если бы мы соединили миллионы этих нейронов вместе?
Как построить свою первую нейросеть
С помощью статьи PhD Оксфордского университета и автора книг о глубоком обучении Эндрю Траска показываем, как написать простую нейронную сеть на Python. Она умещается всего в девять строчек кода и выглядит вот так:
from numpy import exp, array, random, dot
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
random.seed(1)
synaptic_weights = 2 * random.random((3, 1)) — 1
for iteration in xrange(10000):
output = 1 / (1 + exp(-(dot(training_set_inputs, synaptic_weights))))
synaptic_weights += dot(training_set_inputs.T, (training_set_outputs — output) * output * (1 — output))
print 1 / (1 + exp(-(dot(array([1, 0, 0]), synaptic_weights))))
Чуть ниже объясним как получается этот код и какой дополнительный код нужен к нему, чтобы нейросеть работала. Но сначала небольшое отступление о нейросетях и их устройстве.
Человеческий мозг состоит из ста миллиардов клеток, которые называются нейронами. Они соединены между собой синапсами. Если через синапсы к нейрону придет достаточное количество нервных импульсов, этот нейрон сработает и передаст нервный импульс дальше. Этот процесс лежит в основе нашего мышления.
Мы можем смоделировать это явление, создав нейронную сеть с помощью компьютера. Нам не нужно воссоздавать все сложные биологические процессы, которые происходят в человеческом мозге на молекулярном уровне, нам достаточно знать, что происходит на более высоких уровнях.
Для этого мы используем математический инструмент — матрицы, которые представляют собой таблицы чисел. Чтобы сделать все как можно проще, мы смоделируем только один нейрон, к которому поступает входная информация из трех источников и есть только один выход (рис. 1). Наша задача — научить нейронную сеть решать задачу, которая изображена на рисунке ниже. Первые четыре примера будут нашим тренировочным набором. Получилось ли у вас увидеть закономерность? Что должно быть на месте вопросительного знака — 0 или 1?
Вы могли заметить, что вывод всегда равен значению левого столбца. Так что ответом будет 1.
Процесс тренировки
Но как научить наш нейрон правильно отвечать на заданный вопрос? Для этого мы зададим каждому входящему сигналу вес, который может быть положительным или отрицательным числом. Если на входе будет сигнал с большим положительным весом или отрицательным весом, то это сильно повлияет на решение нейрона, которое он подаст на выход. Прежде чем мы начнем обучение модели, зададим для каждого примера случайное число в качестве веса. После этого мы можем приняться за тренировочный процесс, который будет выглядеть следующим образом:
В какой-то момент веса достигнут оптимальных значений для тренировочного набора. Если после этого нейрону будет дана новая задача, которая следует такой же закономерности, он должен дать верный ответ.
Формула для вычисления выхода нейронной сети
Итак, что же из себя представляет формула, которая рассчитывает значение выхода нейрона? Для начала мы возьмем взвешенную сумму входных сигналов:
После этого мы нормализуем это выражение, чтобы результат был между 0 и 1. Для этого, в этом примере, я использую математическую функцию, которая называется сигмоидой:
Если мы нарисуем график этой функции, то он будет выглядеть как кривая в форме буквы S (рис. 4).
Подставив первое уравнения во второе, мы получим итоговую формулу выхода нейрона.
Вы можете заметить, что для простоты мы не задаем никаких ограничений на входящие данные, предполагая, что входящий сигнал всегда достаточен для того, чтобы наш нейрон подал сигнал на выход.
Машинное обучение и нейросети
Комплект продвинутых курсов для освоения машинного и глубокого обучения от классических моделей до нейронных сетей. Дополнительная скидка 5% по промокоду BLOG.
Формула корректировки весов
Во время тренировочного цикла (он изображен на рисунке 3) мы постоянно корректируем веса. Но на сколько? Для того, чтобы вычислить это, мы воспользуемся следующей формулой:
Давайте поймем почему формула имеет такой вид. Сначала нам нужно учесть то, что мы хотим скорректировать вес пропорционально размеру ошибки. Далее ошибка умножается на значение, поданное на вход нейрона, что, в нашем случае, 0 или 1. Если на вход был подан 0, то вес не корректируется. И в конце выражение умножается на градиент сигмоиды. Разберемся в последнем шаге по порядку:
Градиент сигмоиды может быть найден по следующей формуле:
Таким образом, подставляя второе уравнение в первое, конечная формула для корректировки весов будет выглядеть следующим образом:
Существуют и другие формулы, которые позволяют нейрону обучаться быстрее, но преимущество этой формулы в том, что она достаточно проста для понимания.
Как написать это на Python
Хотя мы не будем использовать специальные библиотеки для нейронных сетей, мы импортируем следующие 4 метода из математической библиотеки numpy:
Теперь мы можем, например, представить наш тренировочный набор с использованием array():
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])=
training_set_outputs = array([[0, 1, 1, 0]]).T
Теперь мы готовы к более изящной версии кода. После нее добавим несколько финальных замечаний.
Обратите внимание, что на каждой итерации мы обрабатываем весь тренировочный набор одновременно. Таким образом наши переменные все являются матрицами.
Итак, вот полноценно работающий пример нейронной сети, написанный на Python:
from numpy import exp, array, random, dot
class NeuralNetwork():
def __init__(self):
Задаем порождающий элемент для генератора случайных чисел, чтобы он генерировал одинаковые числа при каждом запуске программы
random.seed(1)
Функция сигмоиды, график которой имеет форму буквы S.
Мы используем эту функцию, чтобы нормализовать взвешенную сумму входных сигналов.
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
Производная от функции сигмоиды. Это градиент ее кривой. Его значение указывает насколько нейронная сеть уверена в правильности существующего веса.
def __sigmoid_derivative(self, x):
return x * (1 — x)
Мы тренируем нейронную сеть методом проб и ошибок, каждый раз корректируя вес синапсов.
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
for iteration in xrange(number_of_training_iterations):
Тренировочный набор передается нейронной сети (одному нейрону в нашем случае).
output = self.think(training_set_inputs)
Вычисляем ошибку (разницу между желаемым выходом и выходом, предсказанным нейроном).
error = training_set_outputs — output
Умножаем ошибку на входной сигнал и на градиент сигмоиды. В результате этого, те веса, в которых нейрон не уверен, будут откорректированы сильнее. Входные сигналы, которые равны нулю, не приводят к изменению веса.
adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))
Корректируем веса.
self.synaptic_weights += adjustment
Заставляем наш нейрон подумать.
def think(self, inputs):
Пропускаем входящие данные через нейрон.
return self.__sigmoid(dot(inputs, self.synaptic_weights))
if __name__ == «__main__»:
Инициализируем нейронную сеть, состоящую из одного нейрона.
neural_network = NeuralNetwork()
print «Random starting synaptic weights:
» print neural_network.synaptic_weights
Тренировочный набор для обучения. У нас это 4 примера, состоящих из 3 входящих значений и 1 выходящего значения.
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
Обучаем нейронную сеть на тренировочном наборе, повторяя процесс 10000 раз, каждый раз корректируя веса.
neural_network.train(training_set_inputs, training_set_outputs, 10000)
print «New synaptic weights after training:
» print neural_network.synaptic_weights
Этот код также можно найти на GitHub. Обратите внимание, что если вы используете Python 3, то вам будет нужно заменить команду “xrange” на “range”.
Несколько финальных замечаний
Попробуйте теперь запустить нейронную сеть, используя в терминале эту команду:
Результат должен быть таким:
Random starting synaptic weights:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
New synaptic weights after training:
[[ 9.67299303]
[-0.2078435 ]
[-4.62963669]]
Ура, мы построили простую нейронную сеть с помощью Python!
Сначала нейронная сеть задала себе случайные веса, затем обучилась на тренировочном наборе. После этого она предсказала в качестве ответа 0.99993704 для нового примера [1, 0, 0]. Верный ответ был 1, так что это очень близко к правде!
Традиционные компьютерные программы обычно не способны обучаться. И это то, что делает нейронные сети таким поразительным инструментом: они способны учиться, адаптироваться и реагировать на новые обстоятельства. Точно так же, как и человеческий мозг.
Конечно, мы создали модель всего лишь одного нейрона для решения очень простой задачи. Но что если мы соединим миллионы нейронов? Сможем ли мы таким образом однажды воссоздать реальное сознание?
Машинное обучение и нейросети
Научим вас создавать чат-ботов, нейросети и агента для игры в Pong.
Машинное обучение для начинающих: создание нейронных сетей
Далее будет представлено максимально простое объяснение того, как работают нейронные сети, а также показаны способы их реализации в Python. Приятная новость для новичков – нейронные сети не такие уж и сложные. Термин нейронные сети зачастую используют в разговоре, ссылаясь на какой-то чрезвычайно запутанный концепт. На деле же все намного проще.
Данная статья предназначена для людей, которые ранее не работали с нейронными сетями вообще или же имеют довольно поверхностное понимание того, что это такое. Принцип работы нейронных сетей будет показан на примере их реализации через Python.
Содержание статьи
Создание нейронных блоков
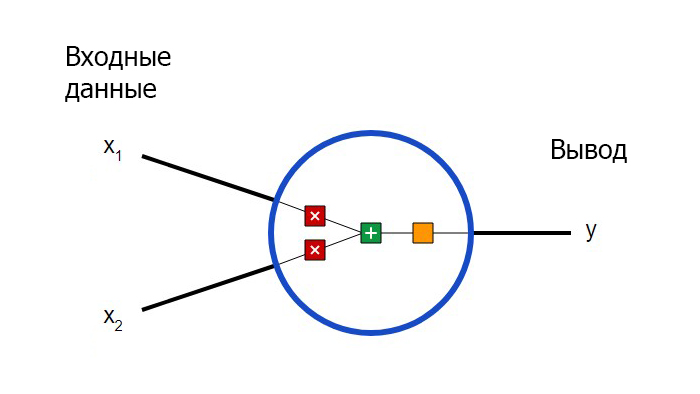
Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным ):
Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым ):
Наконец, сумма передается через функцию активации (на схеме обозначена желтым ):
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:
Простой пример работы с нейронами в Python
Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:
Создание нейрона с нуля в Python
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:
Пример сбор нейронов в нейросеть
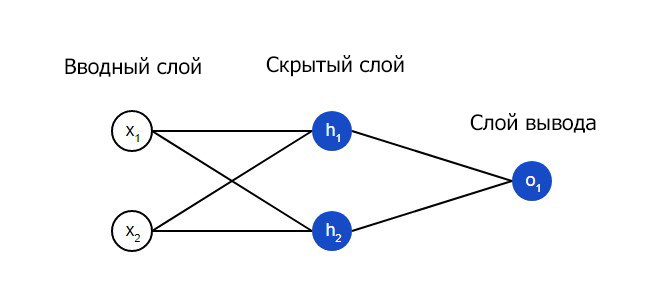
Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:
Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.
Пример прямого распространения FeedForward
Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.
Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.
Создание нейронной сети прямое распространение FeedForward
Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Предположим, у нас есть следующие параметры:
| Имя/Name | Вес/Weight (фунты) | Рост/Height (дюймы) | Пол/Gender |
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
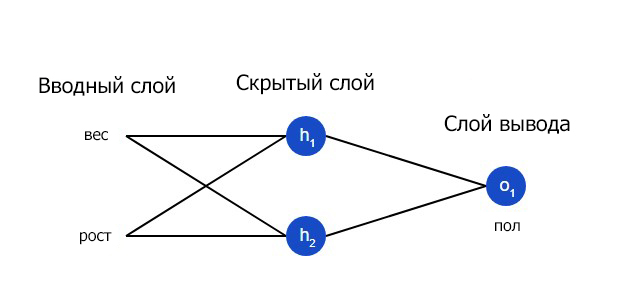
Давайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
Потери
В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:
Лучшие предсказания = Меньшие потери.
Тренировка нейронной сети = стремление к минимизации ее потерь.