Методы перевода десятичного числа в двоичное

В одном из наших материалов мы рассмотрели определение двоичного числа. Оно имеет самый короткий алфавит. Только две цифры: 0 и 1. Примеры алфавитов позиционных систем счисления приведены в таблице.

Позиционные системы счисления

Название системы

Основание

Алфавит

Для перевода небольшого числа из десятичного в двоичное, и обратно, лучше пользоваться следующей таблицей.

Таблица перевода десятичных чисел от 0 до 20 в двоичную систему счисления.

десятичное

число

двоичное число

десятичное

число

двоичное число

Однако таблица получится огромной, если записать туда все числа. Искать среди них нужное число будет уже сложнее. Гораздо проще запомнить несколько алгоритмов перевода чисел из одной позиционной системы счисления в другую.

Как сделать перевод из одной системы счисления в другую? В информатике существует несколько простых способов перевода десятичных чисел в двоичные числа. Рассмотрим два из них.

Способ №1.

Допустим, требуется перевести число 637 десятичной системы в двоичную систему.

Делается это следующим образом: отыскивается максимальная степень двойки, чтобы два в этой степени было меньше или равно исходному числу.

В нашем случае это 9, т.к. 2 9 =512, а 2 10 =1024, что больше нашего начального числа. Таким образом, мы получили число разрядов результата. Оно равно 9+1=10. Значит, результат будет иметь вид 1ххххххххх, где вместо х может стоять 1 или 0.

Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 637-2 9 =125. Затем сравниваем с числом 2 8 =256. Так как 125 меньше 256, то девятый разряд будет 0, т.е. результат уже примет вид 10хххххххх.

2 7 =128 > 125, значит и восьмой разряд будет нулём.

2 6 =64, то седьмой разряд равен 1. 125-64=61 Таким образом, мы получили четыре старших разряда и число примет вид 10011ххххх.

2 5 =32 и видим, что 32 4 =16 1001111ххх. Остаток 29-16=13.

2 3 =8 10011111хх. 13-8=5

2 2 =4 10011111хх, остаток 5-4=1.

2 1 =2 > 1 => 100111110х, остаток 2-1=1.

2 0 =1 => 1001111101.

Это и будет конечный результат.

Способ №2.

Правило перевода целых десятичных чисел в двоичную систему счисления, гласит:

Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков. Записывать его начинаем с последнего найденного.

Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

Получили 11₁₀=1011₂.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

Источник

Как проводится перевод числа из десятичной системы в двоичную?

Содержание:

Перевод из десятичной в двоичную систему исчисления проводится несложно. Для этого действия есть собственный специализированный алгоритм, который мы рассмотрим чуть ниже.

Перевод из десятичной в двоичную систему: целые числа

Пример, как осуществляется перевод из десятичной в двоичную систему

Перевод из десятичной в двоичную систему: дробные числа

Здесь тоже не все может быть сразу понятно, но взглянув на пример, все сразу станет ясно.

Пример, как осуществляется перевод дробного десятичного числа в двоичную систему

Эту конвертацию можно осуществлять до того момента, пока мы не добьемся нужного уровня погрешности. Но для демонстрации алгоритма конвертации этого достаточно. В результате мы получили, что десятичное число 0,234 в двоичном исчислении будет равняться 0011101111100.

А как конвертировать дробное число, если у него в целой части будет какое-то другое значение, кроме 0? Например нам нужно конвертировать число 10,25. В этом случае целая и дробная части будут переводиться раздельно:

Вот что мы получим по факту:

В конце наших вычислений мы получим, что десятичное число 10,25 в двоичной форме будет выглядеть вот так — 1010,01. Кстати, если внимательно посмотреть, то видно, что при конвертации в двоичную форму дробной части нашего примера (при умножении на 2), дробная часть стала равняться 0, поэтому вычисления закончились.

Источник

Перевод из десятичной системы счисления в двоичную

Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:

Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.

Алгоритм перевода целых десятичных чисел в двоичную систему счисления

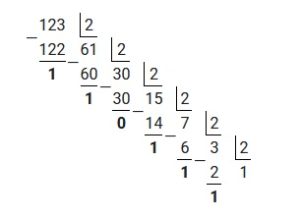
Пример 1 : перевести десятичное число 123 в двоичную систему счисления

Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:

Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.

Алгоритм перевода десятичной дроби в двоичную систему

Пример 2: перевести число 0,123 в двоичную систему.

Решение будет выглядеть следующим образом:

0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)

В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.

Перевод дробного десятичного числа в двоичную систему

Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.

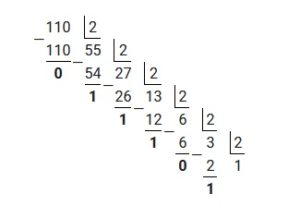
Пример 3: перевести число 110,625 из десятичной системы в двоичную

Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:

Перевод десятичной дроби 0,625 выглядит так:

0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)

Теперь осталось соединить результаты перевода. Таким образом: 110.625₁₀=1101110.101₂

Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.

Источник

Напишите правило перехода десятичных чисел в двоичный код.

Можно записать две похожих формулировки правила перевода из десятичной системы в двоичную:

Формулировка 1. Для перевода чисел из десятичной системы в двоичную нужно разделить число на 2, где 2 — основание двоичной системы, и записать остаток от деления. Полученное частное снова разделить на 2 и также записать остаток. Повторять действия, пока частное не станет равным 0. Записать все остатки в обратном порядке.

Пример 1: переведем число 36 в двоичную систему счисления:

36 / 2 = 18в остатке 0
18 / 2 = 9в остатке 0
9 / 2 = 4в остатке 1
4 / 2 = 2в остатке 0
2 / 2 = 1в остатке 0
1 / 2 = 0в остатке 1
И запишем полученные остатки снизу вверх ↑

Формулировка 2. Для перевода чисел из десятичной системы в двоичную нужно разделить число на 2, где 2 — основание двоичной системы, и записать остаток от деления. Полученное частное снова разделить на 2 и также записать остаток. Повторять действия, пока частное не станет равным 1. Записать последнее частное (1) и все остатки в обратном порядке.

Пример 2: переведем число 123 в двоичную систему счисления:

123 / 2 = 61в остатке 1
61 / 2 = 30в остатке 1
30 / 2 = 15в остатке 0
15 / 2 = 7в остатке 1
7 / 2 = 3в остатке 1
3 / 2 = 1в остатке 1
Последняя цифра — 1
И запишем эту последнюю 1 и остатки снизу вверх ↑

И в целом, первое правило более универсальное, оно подходит ко всем системам, выучите его и забудьте все прочие, чему бы там не учили в школе.

Последняя цифра двоичного числа будет нулем, если число четное и единицей, если число нечетное.

Проверить полученные значения можно с помощью стандартного калькулятора в любой операционной системе. Системы счисления в калькуляторе обозначаются сокращенно: дес — десятичная, бин — двоичная, ост — восьмеричная, хекс — шестнадцатеричная.

Электронное устройство, осуществляющее подобный перевод, называется шифратором.

Шифратор или кодер — логическое устройство, выполняющее логическую функцию (операцию) преобразования позиционного н-разрядного кода в м-разрядный двоичный, то есть на выходных линиях такой микросхемы появляется двоичный код, соответствующий десятичному номеру входной линии.

Источник

Напишите правило перехода десятичных чисел в двоичный код.

Можно записать две похожих формулировки правила перевода из десятичной системы в двоичную:

Формулировка 1. Для перевода чисел из десятичной системы в двоичную нужно разделить число на 2, где 2 — основание двоичной системы, и записать остаток от деления. Полученное частное снова разделить на 2 и также записать остаток. Повторять действия, пока частное не станет равным 0. Записать все остатки в обратном порядке.

Пример 1: переведем число 36 в двоичную систему счисления:

36 / 2 = 18в остатке 0
18 / 2 = 9в остатке 0
9 / 2 = 4в остатке 1
4 / 2 = 2в остатке 0
2 / 2 = 1в остатке 0
1 / 2 = 0в остатке 1
И запишем полученные остатки снизу вверх ↑

Формулировка 2. Для перевода чисел из десятичной системы в двоичную нужно разделить число на 2, где 2 — основание двоичной системы, и записать остаток от деления. Полученное частное снова разделить на 2 и также записать остаток. Повторять действия, пока частное не станет равным 1. Записать последнее частное (1) и все остатки в обратном порядке.

Пример 2: переведем число 123 в двоичную систему счисления:

123 / 2 = 61в остатке 1
61 / 2 = 30в остатке 1
30 / 2 = 15в остатке 0
15 / 2 = 7в остатке 1
7 / 2 = 3в остатке 1
3 / 2 = 1в остатке 1
Последняя цифра — 1
И запишем эту последнюю 1 и остатки снизу вверх ↑

И в целом, первое правило более универсальное, оно подходит ко всем системам, выучите его и забудьте все прочие, чему бы там не учили в школе.

Последняя цифра двоичного числа будет нулем, если число четное и единицей, если число нечетное.

Проверить полученные значения можно с помощью стандартного калькулятора в любой операционной системе. Системы счисления в калькуляторе обозначаются сокращенно: дес — десятичная, бин — двоичная, ост — восьмеричная, хекс — шестнадцатеричная.

Электронное устройство, осуществляющее подобный перевод, называется шифратором.

Шифратор или кодер — логическое устройство, выполняющее логическую функцию (операцию) преобразования позиционного н-разрядного кода в м-разрядный двоичный, то есть на выходных линиях такой микросхемы появляется двоичный код, соответствующий десятичному номеру входной линии.

Источник