линейные коды общего вида

Линейные коды общего вида

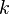
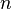
Линейный блоковый код — такой код, что множество его кодовых слов образует -мерное линейное подпространство (назовём его ) в -мерном линейном пространстве, изоморфноепространству -битных векторов.

Это значит, что операция кодирования соответствует умножению исходного 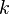-битного вектора на невырожденную матрицу , называемую порождающей матрицей.

Пусть — ортогональное подпространство по отношению к , а — матрица, задающая базис этого подпространства. Тогда для любого вектора справедливо:

Минимальное расстояние и корректирующая способность

Основная статья: Расстояние Хемминга

Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами и называется количество отличных бит на соответствующих позициях:

.

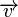
Минимальное расстояние Хемминга является важной характеристикой линейного блокового кода. Она показывает, насколько «далеко» расположены коды друг от друга. Она определяет другую, не менее важную характеристику — корректирующую способность:

.

Корректирующая способность определяет, сколько ошибок передачи кода (типа ) можно гарантированно исправить. То есть вокруг каждого кодового слова имеем -окрестность , которая состоит из всех возможных вариантов передачи кодового слова с числом ошибок ( ) не более . Никакие две окрестности двух любых кодовых слов не пересекаются друг с другом, так как расстояние между кодовыми словами (то есть центрами этих окрестностей) всегда больше двух их радиусов .

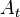
Таким образом, получив искажённую кодовую комбинацию из 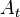, декодер принимает решение, что исходной была кодовая комбинация , исправляя тем самым не более ошибок.

Поясним на примере. Предположим, что есть два кодовых слова и , расстояние Хемминга между ними равно 3. Если было передано слово , и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову , чем к любому другому, и, в частности, к . Но если каналом были внесены ошибки в двух битах (в которых отличалось от ), то результат ошибочной передачи окажется ближе к , чем , и декодер примет решение, что передавалось слово .

Коды Хемминга

Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, чтосиндром

, где — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.

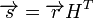
В вычислительной технике и сетях передачи данных би́том чётности (англ. Parity bit) называют контрольный бит, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).

Применение

В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCIIсимволы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода/вывода операционной системы)

Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка, будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило, к каждому байту, что дает коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.

Источник

Линейные коды и способы модуляции

Преобразование к троичным кодам

Последовательность чисел от 0 до 15 можно закодировать и передать с помощью четырех битов. При троичных кодах для этого потребуется только три разряда. Таким образом, требуемая скорость (в битах) в канале уменьшается и составляет только часть от скорости, требуемой для передачи двоичными кодами. Например, если при передаче двоичными кодами требуется скорость 160 бит /с, то при троичном коде 4B3T (когда 4 двоичных символа передаются с помощью 3 троичных символов) — только 120 бит /c. Одно из частных преимуществ троичного кодирования состоит в избыточности кода. Три троичных символа дают 27 комбинаций, а четыре двоичных — 16. Поэтому для передачи многим двоичным комбинациям можно сопоставить по две троичных комбинации. Это делается для несбалансированных кодов, т.е. тех, в которых преобладают сигналы положительной или отрицательной полярности. Тогда второй код выбирается с обратной балансировкой, и их попеременная передача обеспечивает отсутствие постоянной составляющей в линии. Те коды, которые не имеют второго варианта, выбираются из множества сбалансированных комбинаций, как это показано в табл. 9.3. Этот код получил обозначение 4B3T (так как преобразует четыре двоичных символа в 3 троичных).

Эта тенденция получила дальнейшее развитие в своем применении для расширения пропускной способности канала многоуровневых кодов.

Многоуровневые коды

Основное применение многоуровневые коды получили на абонентских участках для повышения скорости передачи двоичных символов.

В этом случае можно говорить не о повышении скорости передачи по каналу, а об увеличении информационного содержания каждого символа.

Объем передаваемой информации в единицу времени в двоичных символах достигает

,

— число уровней, из которых можно производить выбор в каждом такте;

— длительность тактового интервала.

Эта формула показывает скорость передаваемой информации в единицу времени в двоичных символах.

Ее размерность определяется в бит /с.

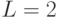
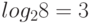
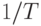
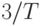
При она действительно равна частоте тактовых импульсов. При 2″ style=»display: inline; «> она показывает, сколько двоичных символов переносит многоуровневый сигнал в секунду. Это иллюстрирует рис.9.3. Каждый один из восьми уровней имеет двоичную нумерацию бита. Если импульсы идут с частотой , то скорость передачи бит /с.

При использовании кодеками недвоичных систем исчисления, например десятичной системы, информационная скорость может возрасти еще больше. Скорость передачи в многоуровневых кодах часто измеряют в бодах, при двоичном сигнале она совпадает со скоростью, передаваемой в битах.

Таблица 9.4. Пример трехуровневого кодирования

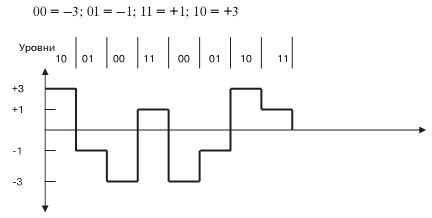
1	0	0	1	0	0	1	1	0	0	0	1	1	0	1	1
+3		–1		–3		+1		–3		–1		+3		+1

На рис. 9.3 показан пример передачи четырехуровневого сигнала, при котором за один такт передается два двоичных бита (содержание бода — два бита). Несмотря на более высокую скорость передачи информации, достигнутую благодаря повышенной информационной емкости символа, многоуровневая передача не применяется. Выше уже было отмечено, что помехи и шумы в канале, а также ограничения на уровень сигнала в усилителях воздействуют прежде всего на амплитуду. Поэтому рассматриваемый способ не нашел применения. Однако в сочетании с другими способами (в частности, частотной модуляцией) он дает высокий эффект и хорошую помехоустойчивость. Наибольшее распространение получило сочетание многоуровневой передачи постоянными импульсами совместно с частотной фазовой манипуляцией. Это позволило резко расширить полосу пропускания на абонентском участке. В следующем параграфе рассмотрен один из таких способов.

Способы модуляции

Модуляция — это процесс изменения параметров несущей частоты (амплитуды, частоты или фазы) по заданному закону. Она осуществляется с более низкой скоростью по сравнению с периодом высокочастотного колебания.

Принято выделять еще один способ передачи информации по каналу.

Манипуляция — процесс воздействия на несущую частоту с помощью входного цифрового сигнала с целью изменения ее параметров (амплитуды, частоты, фазы). К настоящему времени имеется большое число способов модуляции и манипуляции. Ниже изложены некоторые способы, которые будут употребляться в рассматриваемых далее приложениях

Источник

Линейные коды общего вида

Двоичные коды строятся с использованием только двух элементов. В литературе встречаются различные условные обозначения символов двоичного кода. Наиболее употребительные из них рекомендованы МСЭ-Т и представлены в Табл. 6.7.

При реализации кодов необходимо представлять их символы в виде элементов дискретного сигнала той или иной формы, удобной для выполнения последующих операций и передачи по линиям связи.

Формы цифровых сигналов, предназначенных для передачи по линии связи, получили наименование линейных кодов (ЛК). ЛК применяются для передачи данных без модуляции в первичной полосе частот, начинающейся с нуля. Иначе говоря, кадры цифровых систем передачи, сформированные в соответствии с правилами ПЦИ или СЦИ и представляющие собой обычные двоичные последовательности, перед подачей в линию связи подвергаются соответствующему преобразованию в линейном кодере.

Рассмотрим основные типы линейных кодов.

Смысл скремблирования состоит в получении последовательности, в которой статистика появления нулей и единиц приближается к случайной, что позволяет удовлетворять требованиям надежного выделения тактовой частоты и постоянной, сосредоточенной в заданной области частот спектральной плотности мощности передаваемого сигнала.

Заметим, что скремблирование широко применяется во многих видах систем связи для улучшения статистических свойств сигнала. Обычно скремблирование осуществляется непосредственно перед модуляцией.

Особенностью скремблера СС (Рис. 6.52) является то, что он управляется скремблированной последовательностью, т.е. той, которая передается в канал. Поэтому при данном виде скремблирования не требуется специальной установки состояний скремблера и дескремблера; скремблированная последовательность записывается в регистры сдвига скремблера и дескремблера, устанавливая их в идентичное состояние. При потере синхронизма между скремблером и дескремблером время восстановления синхронизма не превышает числа тактов, равного числу ячеек регистра скремблера.

Рис. 6.52. Самосинхронизирующиеся скремблер и дескремблер

Второй недостаток СС скремблера связан с возможностью появления на его выходе при определенных условиях так называемых критических ситуаций, когда выходная последовательность приобретает периодический характер с периодом, меньшим длины ПСП. Чтобы предотвратить это, в скремблере и дескремблере согласно рекомендациям МСЭ-Т предусматриваются специальные дополнительные схемы контроля, которые выявляют наличие периодичности элементов на входе и нарушают ее.

Рис. 6.50. Аддитивные скремблер и дескремблер

Суммируемые в скремблере последовательности независимы, поэтому их период всегда равен наименьшему общему краткому величин периодов входной последовательности и ПСП и критическое состояние отсутствует. Отсутствие эффекта размножения ошибок и необходимости в специальной логике защиты от нежелательных ситуаций делают способ аддитивного скремблирования предпочтительнее, если не учитывать затрат на решение задачи фазирования скремблера и дескремблер. В качестве сигнала установки в ЦСП используют сигнал цикловой синхронизации.

Источник

Систематические корректирующие коды. Линейно групповой код

В данной публикации будет рассматриваться линейно групповой код, как один из представителей систематических корректирующих кодов и предложена его реализация на C++.

Что из себя представляет корректирующий код. Корректирующий код – это код направленный на обнаружение и исправление ошибок. А систематические коды — Это коды, в которых контрольные и информационные разряды размещаются по определенной системе. Одним из таких примеров может служить Код Хэмминга или собственно линейно групповые коды.
Линейно групповой код состоит из информационных бит и контрольных. Например, для исходной комбинации в 4 символа, линейно групповой код будет выглядеть вот так:

Где первые 4 символа это наша исходная комбинация, а последние 3 символа это контрольные биты.

Общая длина линейно группового кода составляет 7 символов. Если число бит исходной комбинации нам известно, то чтобы вычислить число проверочных бит, необходимо воспользоваться формулой:

Где n — это число информационных бит, то есть длина исходной комбинации, и log по основанию 2. И общая длина N кода будет вычисляться по формуле:

Допустим исходная комбинация будет составлять 10 бит.

d всегда округляется в большую сторону, и d=4.

И полная длина кода будет составлять 14 бит.

Разобравшись с длиной кода, нам необходимо составить производящую и проверочную матрицу.

Производящая матрица, размерностью N на n, где N — это длина линейно группового кода, а n — это длина информационной части линейно группового кода. По факту производящая матрица представляет из себя две матрицы: единичную размерностью m на m, и матрицу контрольных бит размерностью d на n. Если единичная матрица составляется путём расставления единиц по главной диагонали, то составление «контрольной» части матрицы имеет некоторые правила. Проще объяснить на примере. Мы возьмем уже известную нам комбинацию из 10 информационных битов, но добавим коду избыточность, и добавим ему 5-ый контрольный бит. Матрица будет иметь размерность 15 на 10.

«Контрольная» часть составляется по схеме уменьшения двоичного числа и соблюдения минимального кодового расстояния между строками: в нашем случае это 11111, 11110, 11101…
Минимальное кодовое расстояние для комбинации будет вычисляться по формуле:

Где r – это ранг обнаруживаемой ошибки, а s – ранг исправляемой ошибки.
В нашем случае ранг исправляемой и обнаруживаемой ошибки 1.
Также необходимо составить проверочную матрицу. Она составляется путём транспонирования «контрольной» части и после неё добавляется единичная матрица размерности d на d.

Составив матрицы, мы уже можем написать линейно групповой код, путём суммирования строк производящей матрицы под номерами ненулевых бит исходного сообщения.

Рассмотрим этот этап на примере исходного сообщения 1001101010.

Линейно групповой код: 100110101011100

Сразу обозначим, что контрольные разряды в ЛГК определяются по правилам чётности суммы соответствующих индексов, в нашем случае, эти суммы составляют: 5,3,3,4,4. Следовательно, контрольная часть кода выглядит: 11100.

В результате мы составили линейно групповой код. Однако, как уже говорилось ранее, линейно групповой код имеет исправляющую способность, в нашем случае, он способен обнаружить и исправить одиночную ошибку.

Допустим, наш код был отправлен с ошибкой в 6-ом разряде. Для определения ошибок в коде служит, уже ранее составленная проверочная матрица

Для того, чтобы определить, в каком конкретно разряде произошла ошибка, нам необходимо узнать «синдром ошибки». Синдром ошибки вычисляется методом проверок по ненулевым позициям проверочной матрицы на чётность. В нашем случае этих проверок пять, и мы проводим наше полученное сообщение через все эти проверки.

Получив двоичное число, мы сверяем его со столбцами проверочной матрицы. Как только находим соответствующий «синдром», определяем его индекс, и выполняем инверсию бита по полученному индексу.

В нашем случае синдром равен: 01111, что соответствует 6-му разряду в ЛГК. Мы инвертируем бит и получаем корректный линейно групповой код.

Декодирование скорректированного ЛГК происходит путём простого удаления контрольных бит. После удаления контрольных разрядов ЛГК мы получаем исходную комбинацию, которая была отправлена на кодировку.

В заключение можно сказать, что такие корректирующие коды как линейно групповые коды, Код Хэмминга уже достаточно устарели, и в своей эффективности однозначно уступят своим современным альтернативам. Однако они вполне справляются с задачей познакомиться с процессом кодирования двоичных кодов и методом исправления ошибок в результате воздействия помех на канал связи.

Реализация работы с ЛГК на C++:

1. StudFiles – файловый архив студентов [Электронный ресурс] studfiles.net/preview/4514583/page:2/.

2. Задачник по теории информации и кодированию [Текст] / В.П. Цымбал. – Изд. объед. «Вища школа», 1976. – 276 с.

3. Тенников, Ф.Е. Теоретические основы информационной техники / Ф.Е. Тенников. – М.: Энергия, 1971. – 424 с.

Источник