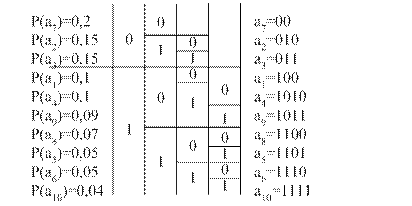код шеннона фано код хаффмана

Сравнительная характеристика Шеннона-Фано и Хаффмана (кодов)

Primary tabs

Forums:

Методика Шеннона–Фано не всегда приводит к однозначному построению кода.
Ведь при разбиении на подгруппы на 1-й итерации можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. В результате среднее число символов на букву окажется другим.
Таким образом, построенный код может оказаться не самым лучшим.

От указанного недостатка свободна методика Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Метод Хаффмана производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Результаты эффективного кодирования по методу Хаффмана всегда лучше результатов кодирования по методу Шеннона-Фано.

Предложенный Хаффманом алгоритм построения оптимальных неравномерных кодов – одно из самых важных достижений теории информации, как с теоретической, так и с прикладной точек зрения. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия.

Трудно поверить, но этот алгоритм был придуман в 1952 г. студентом Дэвидом Хаффманом в процессе выполнения домашнего задания =).

Кодирование методом Хаффмана называют двухпроходным, так как его реализация распадается на два этапа:

Источник

Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана.

Код Шеннона-Фано

Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.

Рис. Кодовое дерево кода Шеннона – Фано

Методика Шеннона – Фано не всегда приводит к однозначному построе­нию кода, поскольку при разбиении на части можно сделать больше по веро­ятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспе­чивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмечен­ных недостатков.

Код Хаффмана

Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответ­ствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последователь­ное ветвление продолжается до тех пор, пока не дойдем до вероятности каж­дой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.

Источник

2.1. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды

Параллельно должна решаться проблема различимости кодов. На выходе кодера получена следующая последовательность элементарных сигналов:

Каким образом она может быть декодирована? Если бы код был равномерным, приемное устройство просто отсчитывало бы заданное (фиксированное) число элементарных сигналов (например, 5, как в коде Бодо) и интерпретировало их в соответствии с кодовой таблицей. При использовании неравномерного кодирования возможны два подхода к обеспечению различимости кодов.

Неравномерный код с разделителем

В соответствии с перечисленными правилами строится кодовая табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 1.3) вероятностях появления отдельных букв.

Теперь по формуле нахождения среднего для значений случайных независимых величин можно найти среднюю длину кода К(r,2) для данного способа кодирования:

Поскольку для русского языка I₁ ( r ) = 4,356 бит, избыточность данного кода, согласно (3.9), составляет:

это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение К(е,2) = 4,716, что при I₁ ( e ) = 4,036 бит приводят к избыточности кода Q(е,2) = 0,168.

Рассмотрев один из вариантов двоичного неравномерного кодирования, необходимо ответить на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?

Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.

Пусть имеется следующая таблица префиксных кодов:

Требуется декодировать сообщение:

Декодирование производится циклическим повторением следующих действий:

(a) отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;

(b) сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (а);

(c) декодировать рабочее кодовое слово, очистить его;

(d) проверить, имеются ли еще знаки в сообщении; если «да», перейти к (а).

Применение данного алгоритма дает:

Рис. 3.1. Результат применения алгоритма

Доведя процедуру до конца, получается сообщение: «мама мыла раму».

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.

Префиксный код Шеннона-Фано

Процедура построения кодов

Из процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, код является префиксным. Средняя длина кода равна:

I₁ ( A ) = 2,390 бит. Подставляя указанные значения в (3.5), получается избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%. Однако, данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (0,35 и 0,65, соответственно). Применение изложенной схемы построения к русскому алфавиту дает избыточность кода 0,0147.

Префиксный код Хаффмана

Рис. 3.2. Процедура построения кодов

К(А,2) = 0,3 ∙ 2 + 0,2 ∙ 2 + 0,2 ∙ 2 +0,15 ∙ 3 + 0,1 ∙ 4 + 0,05 ∙ 4 = 2,45. (3.13)

Рис. 3.3. Обратная процедура построения кодов

Избыточность снова оказывается равной Q(A, 2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона-Фано становится очевидной, если сравнить избыточности кодов для какого-либо естественного языка. Применение описанного метода для букв русского алфавита порождает коды, представленные в табл. 3.4. (для удобства сопоставления они приведены в формате табл. 3.1).

Коды для букв русского алфавита

Средняя длина кода оказывается равной К(r,2) = 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано (см. выше).

Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.

Источник

27. Код Шеннона-Фано. Код Хаффмана.

koralexand.ru > 27. Код Шеннона-Фано. Код Хаффмана.

Код Шеннона-Фано

Код строится следующим образом:

1) буквы алфавита сообщений выпи­сываются в таблицу в порядке убывания вероятностей;

2) затем они разделя­ются на две группы так, чтобы суммы вероятностей в каждой из групп бы­ли по возможности одинаковы;

3) всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним — 0;

4) каждая из получен­ных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д.

Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Пример. Рассмотрим алфавит из восьми букв (табл. 12). При обычном (не учитывающем статистических характеристик) кодировании для пред­ставления каждой буквы требуется три символа.

Таблица 8.12 Таблица 13

Буквы	Вероят­ности	Кодовые комбинации	Буквы	Вероят­ности	Кодовые комбинации
0,22	11	0,22	11
0,20	101	0,20	10
0,16	100	0,16	011
0,16	01	0,16	010
0,10	001	0,10	001
0,10	0001	0,10	0001
0,04	00001	0,04	00001
0,02	00000	0,02	00000

Вычислим энтропию набора букв: Н

и среднее число символов на букву

где n() — число символов в кодовой комбинации, соответствующей букве.

Значения Н(z) и l_ср не очень различаются по величине. Условие теоремы Шеннона выполнено Н(z) 2 неопределенность ста­новится еще больше.

Метод Хаффмена

Метод Хаффмена свободен от недостатка связанного с неоднозначностью построения кода. Данная методика также использует статистические свойства источника сообщений. Метод гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

В таблице 14 показаны основные шаги построения кода.

Буквы	Вероятности	Вспомогательные столбцы
		1	2	3	4	5	6	7
0,22	0,22	0,22	0,26	0,32	0,42	0,58	1
0,20	0,20	0,20	0,22	0,26	0,32	0,42
0,16	0,16	0,16	0,20	0,22	0,26
0,16	0,16	0,16	0,16	0,20
0,10	0,10	0,16	0,16
0,10	0,10	0,10
0,04	0,06
0,02

Для двоичного кода методика сводится к следующему:

1) Буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероят­ностей;

2) две последние буквы объединяются в одну вспомогательную бук­ву, которой приписывается суммарная вероятность;

3) вероятности букв, не участвовавших в объединении, и полу­ченная суммарная вероятность снова располагаются в порядке убывания ве­роятностей в дополнительном столбце, а две последние буквы снова объединяются.

Процесс продолжается до тех пор, пока не полу­чим единственную вспомогательную букву с вероятностью, равной единице.

Для составления кодовой комбина­ции, соответствующей данному сообще­нию, необходимо проследить путь пере­хода сообщений по строкам и столбцам таблицы. Для наглядности строится кодо­вое дерево(рис.1).

Рис.1 Кодовое дерево

Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей — 0. Такое последовательное ветвление продолжается до тех пор, пока не дойдем до каждой буквы (рис. 1).

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию;

01 00 111 110 100 1011 10101 10100

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

Кодирование Шеннона-Фано

Алгоритм Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона-Фано префиксные, то есть, никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.

Содержание

Основные сведения

Кодирование Шеннона-Фано (англ. Shannon-Fano coding) — алгоритм префиксного неоднородного кодирования. Относится к вероятностным методам сжатия (точнее, методам контекстного моделирования нулевого порядка). Подобно алгоритму Хаффмана алгоритм Шеннона-Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями.

Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).

Основные этапы

Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей p₀ − p₁ может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность, большую нуля).

Алгоритм вычисления кодов Шеннона-Фано

Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Все множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.

При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n+1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути еше не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.

Пример кодового дерева

A (частота встречаемости 50), B (частота встречаемости 39), C (частота встречаемости 18), D (частота встречаемости 49), E (частота встречаемости 35), F (частота встречаемости 24).

A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина сжатой последовательности, по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются неоптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным.

Литература

Ссылки

Методы сжатияТеория

Информация	Собственная · Взаимная · Энтропия · Условная энтропия · Сложность · Избыточность
Единицы измерения	Бит · Нат · Ниббл · Хартли · Формула Хартли

Без потерь

Энтропийное сжатие	Алгоритм Хаффмана · Адаптивный алгоритм Хаффмана · Арифметическое кодирование ( Алгоритм Шеннона — Фано · Интервальное) · Коды Голомба · Дельта · Универсальный код (Элиаса · Фибоначчи)
Словарные методы	RLE · · LZ ( · LZSS · LZW · LZWL · · · LZX · LZRW · LZJB · LZT)
Прочее	RLE · CTW · BWT · PPM · DMC

Аудио

Теория	Свёртка · PCM · Алиасинг · Дискретизация · Теорема Котельникова
Методы	LPC (LAR · LSP) · WLPC · CELP · ACELP · A-закон · μ-закон · MDCT · Преобразование Фурье · Психоакустическая модель
Прочее	Dynamic range compression · Сжатие речи · Полосное кодирование

Изображения

Термины	Цветовое пространство · Пиксел · Chroma subsampling · Артефакты сжатия
Методы	RLE · DPCM · Фрактальный · Wavelet · EZW · SPIHT · LP · ДКП · ПКЛ
Прочее	Битрейт · Test images · PSNR · Квантование

Видео

Термины	Характеристики видео · Кадр · Типы кадров · Качество видео
Методы	Компенсация движения · ДКП · Квантование
Прочее	Видеокодек · Rate distortion theory (CBR · ABR · VBR)

См. также: Программы для сжатия данных • Стандарты и форматы сжатия

Полезное

Смотреть что такое «Кодирование Шеннона-Фано» в других словарях:

Алгоритм Шеннона — Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет … Википедия

Код Шеннона-Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм… … Википедия

Кодирование энтропии — кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых… … Википедия

Кодирование с минимальной избыточностью — Кодирование энтропии кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных… … Википедия

Кодирование длин серий — (англ. Run length encoding, RLE) или Кодирование повторов простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд. При кодировании… … Википедия

Кодирование Хаффмана — Алгоритм Хаффмана (англ. Huffman) адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. В настоящее… … Википедия

Шеннона теорема — Теорема Котельникова (в англоязычной литературе теорема Найквиста) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой более… … Википедия

Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия

Алгоритм Шеннона — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Robert Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на… … Википедия

Энтропийное кодирование — Для термина «Кодирование» см. другие значения. Энтропийное кодирование кодирование последовательности значений с возможностью однозначного восстановления с целью уменьшения объёма данных (длины последовательности) с помощью усреднения… … Википедия

Источник