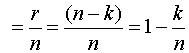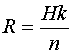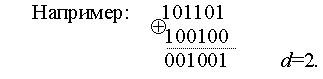код который всегда содержит постоянное количество информационных и контрольных знаков
Код который всегда содержит постоянное количество информационных и контрольных знаков
Классификация рассматриваемых в данной главе методов кодирования приведена на рис. 5.2. Эта классификация не является исчерпывающей, в нее включены лишь некоторые методы, которые широко используются в современных системах связи.
Коды можно разделить на две самостоятельные группы. К первой относятся коды, использующие все возможные комбинации – неизбыточные коды. В литературе их еще называют простыми, или первичными. Ко второй группе относятся коды, использующие лишь определенную часть всех возможных комбинаций, такие коды называются избыточными. Оставшаяся часть комбинаций используется для обнаружения или исправления ошибок, возникающих при передаче сообщений. В этих кодах количество разрядов кодовых комбинаций можно условно разделить на определенное число разрядов, предназначенных для информации (информационные разряды), и число разрядов, предназначенных для коррекции ошибок (проверочные разряды).
Обе группы кодов, в свою очередь, подразделяются на равномерные и неравномерные. Равномерные коды – это коды, все кодовые комбинации которых содержат постоянное количество разрядов. Неравномерные коды содержат кодовые комбинации с различным числом разрядов. Ввиду того что неравномерные избыточные коды не нашли применения на практике из-за сложности их технической реализации, в дальнейшем их рассматривать не будем.
Все корректирующие (избыточные) коды делятся на два больших класса: блочные и непрерывные коды (рис. 5.2).
При кодировании блочным кодом последовательность 




В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. Неразделимые коды не имеют четкого разделения кодовой комбинации на информационные и проверочные символы. К ним относятся коды с постоянным весом и коды Плоткина [2].
Разделимые блочные коды, в свою очередь, делятся на несистематические и систематические. Наиболее многочисленный класс разделимых кодов составляют систематические коды. Основная их особенность в том, что проверочные символы образуются как линейные комбинации информационных символов. К систематическим кодам относятся коды с проверкой на четность, коды с повторением, корреляционный, инверсный, коды Хэмминга, Голея, Рида-Маллера, Макдональда, Варшамова, с малой плотностью проверок на четность, итеративный код [2].
В несистематических кодах проверочные символы представляют собой суммы подблоков с 
Разновидностью систематических кодов являются циклические коды. Кроме всех свойств систематического кода, циклические коды имеют следующее свойство: если некоторая кодовая комбинация принадлежит коду, то получающаяся путем циклической перестановки символов новая комбинация также принадлежит данному коду. К наиболее известным циклическим кодам относятся простейшие коды, коды Хэмминга, Боуза-Чоудхури-Хоквингема, мажоритарные, коды Файра, Абрамсона, Миласа-Абрамсона, Рида-Соломона, компаундные коды.
Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
Электронные средства сбора, обработки и отображения информации
Оглавление
Помехоустойчивое кодирование
Понятие корректирующего кода
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.
Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).
В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.
Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.
Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.
Различают разделимые и неразделимые блоковые коды.
При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.
При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.
Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.
Общие принципы использования избыточности
Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть 





— 
— 

— 


Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:
Кобн 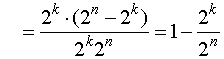
Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит 

Кобн 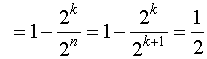
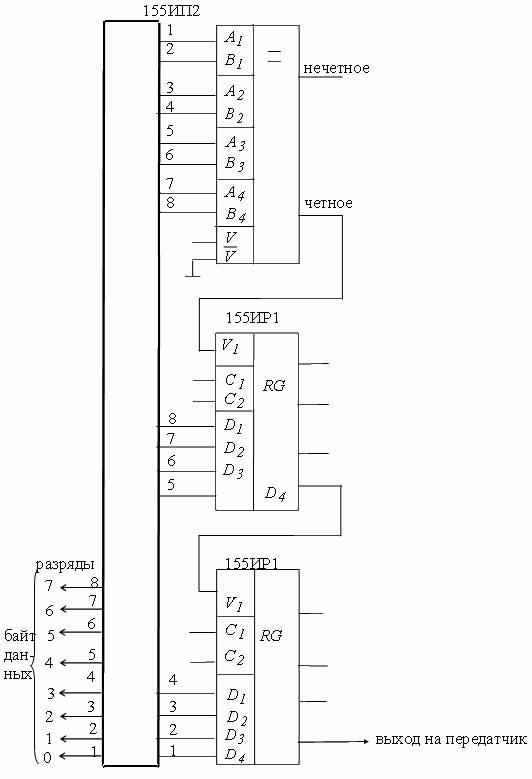
Пример кодирующего устройства с проверкой на четность показан на рис.
Основные параметры корректирующих кодов
Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.
Рассмотрим суть этих параметров.
Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов
Относительной избыточностью корректирующего кода называют величину
отн
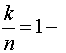
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.
Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна
поскольку в последовательности из п символов только k информационных.
Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.
Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.
Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.
Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.
Число обнаруживаемых ошибок определяется минимальным расстоянием 
В безызбыточном коде все комбинации являются разрешенными, 
Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.
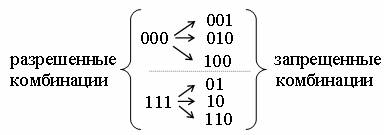
Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как 

Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:
Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.
В общем случае при необходимости обнаруживать ошибки кратности 


В этом случае никакая ошибка кратности 
Ошибки можно не только обнаруживать, но и исправлять.
Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.
Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.
Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:
В общем случае исправляемые ошибки кратности 


где 
Если, например, п=7, 
Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.
Групповой код с проверкой на четность
Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:
Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы 
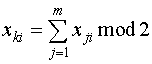
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.
Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).
Если проверка проводится по строкам и столбцам, то код называется матричным.
Проверочные символы располагаются следующим образом:
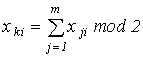
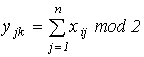
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.
Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.
Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.
Коды с постоянным весом
Весом называется число единиц, содержащихся в кодовых комбинациях.
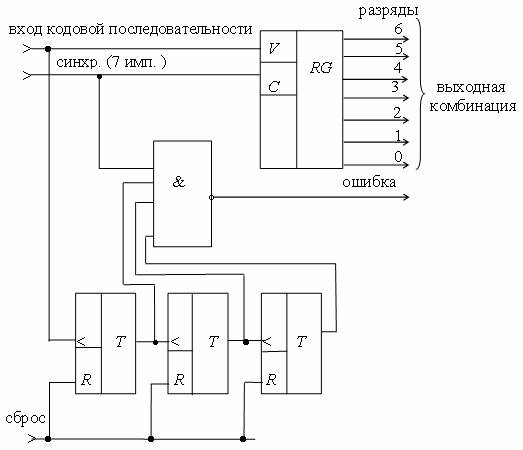
В коде «3 из 7» возможных комбинаций сто двадцать восемь (
Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.
Циклические коды
Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.


Например, комбинация 1001111 (п=7) будет представлена многочленом
При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.
Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.
Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:
Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.
Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=
Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.
Число разрядов регистра выбирается равным степени образующего полинома.
Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.
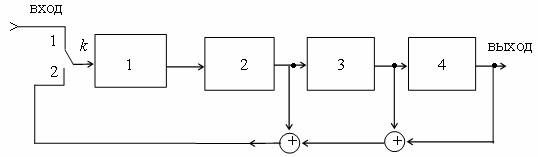
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.
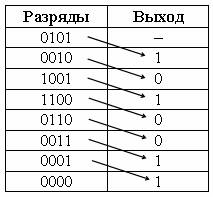
В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.
Свойства циклического кода:
1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;
2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;
Код Хэмминга. Пример работы алгоритма
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:
Стало:
Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее: 
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее: 
и для второй части:
Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно): 
Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину: 
Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.