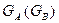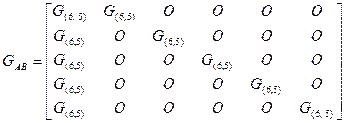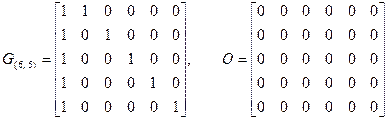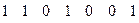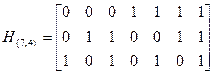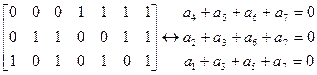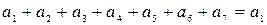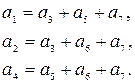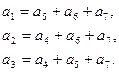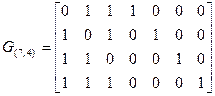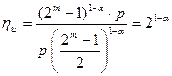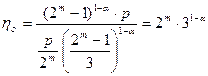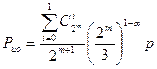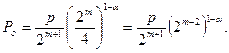какой размер кодового слова может быть у кода хэмминга

Помехоустойчивое кодирование. Коды Хэмминга

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.

Классификация помехоустойчивых кодов

По используемому алфавиту:

Блочные коды делятся на

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

Источник

Код Хэмминга. Пример работы алгоритма

Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.

Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.

Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

Как это работает.

Для того, чтобы понять работу данного алгоритма, рассмотрим пример.

Подготовка

Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.

На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

и

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):

Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».

Вычисление контрольных бит.

Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:

Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.

Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.

Декодирование и исправление ошибок.

Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.

Заключение.

В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.

Примечание.

На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.

Источник

Коды Хэмминга

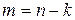
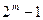
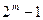
Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H_(n,k), имеющей строк и столбцов, причем столбцами H_(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до ).

Длина кодовой комбинации кода Хэмминга равна .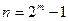

Число информационных элементов определяется как .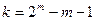

Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.

Зная вид матрицы H_(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбца H_(n,k) не являются линейно зависимыми. Наряду с этим, для любого числа m всегда можно указать три столбца матрицы H_(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэмминга d_min=3.

Код Хэмминга является одним из немногочисленных примеров совершенного кода.

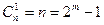
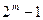
Действительно, поскольку (n, k) – код Хэмминга исправляет все одиночные ошибки, то все образцы одиночных ошибок (а их всего насчитывается вариантов) должны разместиться в различных смежных классах, число которых также равно . Следовательно, помимо смежных классов, содержащих образцы одиночных ошибок, никаких других в таблице декодирования не имеется, что и подтверждает совершенность кода Хэмминга.

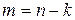
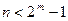
При фиксированном числе можно построить код Хэмминга любой длины () путем укорочения (n, k) – кода. Укорочение не уменьшает минимальное кодовое расстояние. В силу того, что для любого числа n существует код Хэмминга, любой групповой код с исправлением одиночных ошибок принято называть кодом Хэмминга.

Пример 5.13. Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.

m		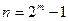k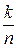
0,33
0,57
0,74
0,84
0,91
0,95

Очевидно, что минимальная длина кода Хэмминга, имеющего практическое значение, есть 3. При увеличении n отношение 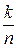возрастает и стремится к 1.

Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:

.

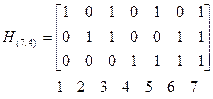
Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3( к примеру 1, 2 и 3), следовательно, d_min=3.

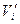
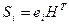
В том случае, когда столбцы матрицы H_(n,k) – кода Хэмминга есть упорядоченная запись m – разрядных двоичных чисел, декодирование осуществляется оригинальным образом. В результате вычисления проверочного соотношения для кодовой комбинации , имеющей одиночную ошибку, получается синдром в точности равный номеру элемента, в котором произошла ошибка.

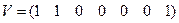
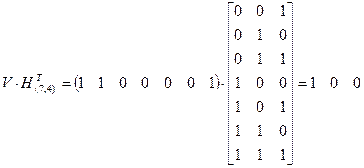
Пример 5.15. Пусть приемник УЗО системы передачи данных зарегистрировал комбинацию . Вычисление синдрома дает

,

т.е. ошибка в четвертом элементе и кодовая комбинация кода (7,4), которая была передана, имеет вид:

Путем несложных преобразований из (n, k) – кода Хэмминга с d_min=3 можно получить (n+1, k) – код Хэмминга с d_min=4.

Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.

Матрица проверок для (n+1, k) – кода Хэмминга с d_min=4 получается из матрицы проверок (n, k) – кода с d_min=3 путем введения дополнительной строки из (n+1)-ой единицы.

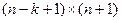
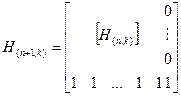
Так как размерность матрицы проверок кода с d_min=4 должна быть равна , то к каждой строке матрицы проверок кода с d_min=3, необходимо добавить один нулевой элемент для того, чтобы не нарушить введенные ранее проверки. Матрица проверок для (n+1, k) – кода d_min=4 имеет вид:

,

Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.

Пример 5.16. Построить код Хэмминга (8,4) с d_min=4 на основе матрицы проверок кода (7,4).

По виду матрицы 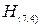можно сделать вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на четность.

Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.

Таким образом, матрице 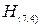соответствует следующая система проверочных соотношений:

Для того, чтобы получить код (8,4) с d_min=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:

.

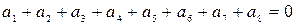
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н_(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н_(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:

.

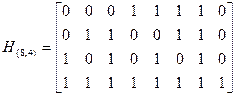
Определим известным способом d_min (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) d_min=4.

Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).

По виду матрицы 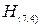, приведенной в предыдущем примере, в качестве проверочных элементов выбираем элементы, которым соответствуют столбцы, содержащие только по одной единице, т.е. первый, второй и четвертый. Следовательно, 4 информационных элемента кода (7,4) должны занимать места 3, 5, 6 и 7-го разрядов. Приведенная в предыдущем примере система проверочных соотношений позволяет определить значение каждого из проверочных элементов по значениям информационных элементов, т.е. по значению элементов простого кода, который необходимо закодировать кодом Хэмминга

Зная места проверочных элементов, легко привести матрицу H_(n,k) кода Хэмминга к канонической форме.

Пример 5.18. Преобразовать матрицу 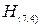к канонической форме.

Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:

.

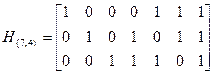
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:

Порождающую матрицу G_{(n, k)} для кода Хэмминга можно получить из матрицы H_(n,k), используя теорему 5.3:

Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.

Оценим эффективность кодов Хэмминга.

а) Коды Хэмминга с dmin=3

Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратности S=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:

.

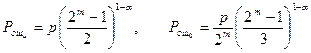
Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:

Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:

Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:

.

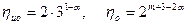
5.4.3Итеративные коды.

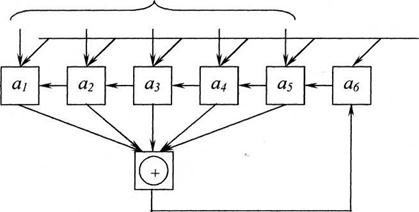
На основе (n, n-1) – кодов с d_min=2 или кодов Хэмминга с d_min=3 и d_min=4 можно построить коды с более высокими корректирующими свойствами. Для этой цели, наряду с защитой каждой передаваемой комбинации описанным выше способом, осуществляют помехоустойчивое кодирование одноименных разрядов групп передаваемых комбинаций. Процесс кодирования можно пояснить при помощи рис. 5.6.

Комбинации простого кода, подлежащие передаче по системе связи, записываются в виде таблицы – каждая комбинация составляет отдельную строку этой таблицы (информационные символы). Затем осуществляется кодирование по строкам и столбцам. В общем случае для кодирования строк и кодирования столбцов можно использовать различные коды. Избыточные элементы дописываются к каждой строке (проверка по строкам) и к каждому столбцу (проверка по столбцам). Проверка проверок осуществляется кодированием столбцов, составленных из избыточных элементов строк или кодированием строк, составленных из проверок столбцов. Последующее введение избыточности осуществляется для защиты блоков информации, представленных на рис. 5.6. Процесс кодирования поясняется на рис. 5.7. Из блоков информации, защищенных двумя проверками, составляется параллелепипед. Избыточные разряды третьей проверки образуют параллелепипед, выделенный утолщенной линией.

5 эл. комбинация

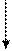В результате итеративного кодирования получаются групповые коды, которые обладают следующим важным свойством.

Теорема 5.3. Минимальное кодовое расстояние итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.

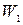
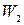
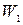
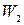
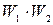
Действительно, если в случае двух проверок минимальный вес одного кода равен , а другого , то вектор итеративного кода имеет, по крайней мере, единиц в каждой строке и элементов в каждом столбце и, следовательно, не менее единиц.

Аналогичные рассуждения можно продолжить и на случай большего числа проверок.

Порождающая матрица итеративного кода может быть построена следующим образом.

Пусть G_A – порождающая матрица кода, используемого для проверки по строкам, а G_В – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (G_AВ) имеет вид:

.

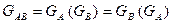
Запись означает, что на местах “1” в матрице G_A записывается матрица G_В, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам G_В. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то

,

.

Источник