как закодировать картинку в двоичный код
Двоичное кодирование графической информации
Важным этапом кодирования графического изображения является разбиение его на дискретные элементы (дискретизация).
Основными способами представления графики для ее хранения и обработки с помощью компьютера являются растровые и векторные изображения.
Векторное изображение представляет собой графический объект, состоящий из элементарных геометрических фигур (чаще всего отрезков и дуг). Положение этих элементарных отрезков определяется координатами точек и величиной радиуса. Для каждой линии указывается двоичные коды типа линии (сплошная, пунктирная, штрихпунктирная), толщины и цвета.
Растровое изображение представляет собой совокупность точек (пикселей), полученных в результате дискретизации изображения в соответствии с матричным принципом.
Матричный принцип кодирования графических изображений заключается в том, что изображение разбивается на заданное количество строк и столбцов. Затем каждый элемент полученной сетки кодируется по выбранному правилу.
В соответствии с матричным принципом строятся изображения, выводимые на принтер, отображаемые на экране дисплея, получаемые с помощью сканера.
Качество изображения будет тем выше, чем «плотнее» расположены пиксели, то есть чем больше разрешающая способность устройства, и чем точнее закодирован цвет каждого из них.
Для черно-белого изображения код цвета каждого пикселя задается одним битом.
Если рисунок цветной, то для каждой точки задается двоичный код ее цвета.
Графическая информация, как и информация любого другого типа, хранятся в памяти компьютера в виде двоичных кодов. Изображение, состоящее из отдельных точек, каждая из которых имеет свой цвет, называется растровым изображением. Минимальный элемент такого изображения в полиграфии называется растр, а при отображении графики на мониторе минимальный элемент изображения называют пиксель (pix).
 | |
| Пиксель | Растр |
Рис. 4.1. Минимальная единица изображения: пиксель и растр.
Если пиксель изображения может быть раскрашен только в один из 2х цветов, допустим, либо в черный (0), либо в белый (1), то для хранения информации о цвете пикселя достаточно 1 бита памяти (log2(2)=1 бит). Соответственно, объем, занимаемый в памяти компьютера всем изображением, будет равен числу пикселей в этом изображении (рис. 20а).
Если под хранение информации о цвете пикселя выделить 2 бита, то число цветов, допустимых для раскраски каждого пикселя, увеличится до 4х (N=2 2 =4), а объем файла изображения в битах будет вдвое больше, чем количество составляющих его пикселей (рис. 20b).
 |  |
| Рис. 4.2. 1 бит на пиксель – 2 цвета. | Рис. 4.3. 2 бита на пиксель – 4 цвета. |
При печати на не цветном принтере обычно допускает 256 градаций серого цвета (от черного (0) до белого (255)) для раскраски каждой точки изображения. Под хранение информации о цвете точки в этом случае отводится 1 байт, т.е. 8 бит (log2(256)=8 бит).
Восприятие цвета
Способность к цветоощущению возникла в процессе эволюции как реакция адаптации, как способ получения сведений об окружающем мире и способ ориентирования в нем. Каждый человек воспринимает цвета индивидуально, отлично от других людей. Однако у большей части людей цветовые ощущения очень схожи.
Физической основой цветовосприятия является наличие специфических светочувствительных клеток в центральном участке сетчатки глаза, так называемых палочек и колбочек.
Различают три вида колбочек, по чувствительности к разным длинам волн света (цветам). Колбочки S-типа чувствительны в фиолетово-синей, M-типа — в зелено-желтой, и L-типа — в желто-красной частях спектра.
Наличие этих трех видов колбочек (и палочек, чувствительных в изумрудно-зеленой части спектра) даёт человеку цветное зрение.
В ночное время зрение обеспечивают только палочки, поэтому ночью человек не может различать цвета.
Каждое животное видит мир по-своему. Сидя в засаде, лягушка видит только движущиеся предметы: насекомых, на которых она охотится, или своих врагов. Чтобы увидеть всё остальное, она должна сама начать двигаться.
Сумеречные и ночные животные (например, волки и другие хищные звери), как правило, почти не различают цветов.
Стрекоза хорошо различает цвета только нижней половиной глаз, верхняя половина смотрит в небо, на фоне которого добыча и так хорошо заметна.
Цветовые модели
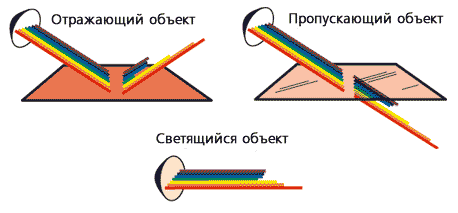
Все объекты окружающего мира можно разделить на: излучающие (светящиеся: солнце, лампа, монитор), отражающие излучение (бумага) и пропускающие (стекло).
Рис. 4.4. Излучающие, отражающие и пропускающие объекты.
В зависимости от того, является объект излучающим или отражающим для представления описания его цвета в виде числового кода используются две обратных друг другу цветовые модели: RGB или CMYK.
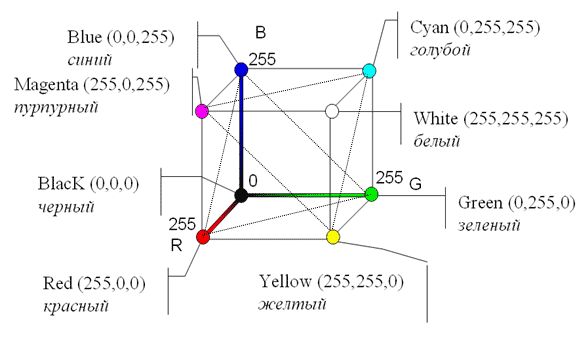
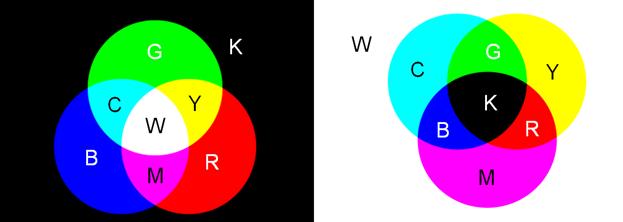
RGB.Модель RGB используется в телевизорах, мониторах, проекторах, сканерах, цифровых фотоаппаратах… Эта модель является аддитивной (суммарной), что означает, что цвета в этой модели добавляются к черному (blacK) цвету.
Основные цвета в этой модели: красный (Red), зеленый (Green), синий (Blue). Их парное сочетание в равных долях дает дополнительные цвета: желтый (Yellow), голубой (Cyan) и пурпурный (Magenta).
Сумма всех трех основных цветов в равных долях дает белый (White) цвет: R+G+B=W.
CMYK. Цветовая модель CMYK используется в полиграфии при формировании изображений, предназначенных для печати на бумаге. Основными цветами в ней являются те, которые являются дополнительными в модели RGB, т.к. они получаются вычитанием цветов RGB из белого цвета. Поэтому модель CMYK называется субтрактивной.
В свою очередь парное сочетание в равных долях цветов модели CMY дает цвета модели RGB. Всем известно, что если смешать на бумаге желтую и голубую краску, получится зеленый цвет. На языке цветовых моделей, это описывается выражением: Y+C=G, кроме того, C+M=B и M+Y=R.
В теории, сумма C+M+Y=K, т.е. дает черный (blacK) цвет, но поскольку реальные типографские краски имеют примеси, их цвет не совпадает в точности с теоретически рассчитанным голубым, желтым и пурпурным. Особенно трудно получить из этих красок черный цвет. Поэтому в модели CMYK к триаде CMY добавляют черный цвет K. От слова blacK для обозначения черного цвета взята последняя буква, и т.к. буква B уже используется в модели RGB для обозначения синего цвета.
 | |
| Рис. 4.5. Излучающий объект RGB. | Рис. 4.5. Отражающий объект CMYK. |
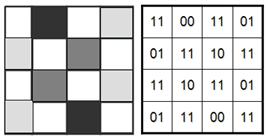
Если кодировать цвет одной точки изображения тремя битами, каждый из которых будет являться признаком присутствия (1) или отсутствия (0) соответствующей компоненты системы RGB, то мы получим все восемь различных цветов описанных выше моделей.
Таблица 4.2. Кодировка цветов
| 1 бит на каждый компонент RGB 2 3 =8 | R | G | B | Цвет |
| W (white /белый) | ||||
| Y (yellow / желтый) | ||||
| M (magenta / пурпурный) | ||||
| R (red / красный) | ||||
| C (cyan / голубой) | ||||
| G (green / зеленый) | ||||
| B (blue /синий) | ||||
| K (black / черный) |
Рис. 4.6. Цветовой куб.
Изменяющиеся в диапазоне от 0 до 255 координаты RGB образуют цветовой куб. Любой цвет расположен внутри этого куба и описывается своим набором координат, показывающем в каких долях смешаны в нем красная, зеленая и синяя составляющие.
Таблица 4.3. Справочная таблица
| Изображение | Основа кодирования | Памяти на пиксель | Кол-во цветов |
| байт | бит | ||
| Черно-белое | Bitmap | ||
| Оттенки серого | 256 градаций серого | 2 8 =256 | |
| Цветное излучающее | RGB | 2 24 =16 777 216 | |
| Цветное отражающее | CMYK | 2 32 =429 4967 296 |
HSB.Две описанные выше модели удобны скорее для компьютеров, чем для нас с вами. Человеку гораздо проще не синтезировать цвет из отдельных составляющих, а выбирать его, ориентируясь на более естественные параметры: тон, насыщенность, яркость. Именно эти три параметра и стали основой для модели HSB (Hue, Saturation, Brightness), она же HSL (Hue, Saturation, Lightness).
Параметр тона Hue (читается «хью») — это чистый цвет сам по себе — один из цветов спектра (радуги). В модели HSB он представлен как замкнутый круг, положение конкретного оттенка на котором указывается в градусах от 0 до 359.
Параметр Saturation — это насыщенность. Чем меньше насыщенность, тем ближе цвет к серому и наоборот: с увеличением насыщенности цвет становится сочнее. Lightness, соответственно, определяет долю белого в итоговом цвете.
Lab.В попытке совместить цветовой охват моделей RGB и CMYK была создана модель Lab, не привязанная к среде вывода. Параметр модели L показывает общую яркость пикселов, параметром a передаются цвета от темно-зеленого до ярко-розового с разными вариациями насыщенности и яркости, а параметром b — от светло-синего до ярко-желтого. Модель Lab обеспечивает наибольшую совместимость, цветовой охват и скорость. Из-за своей универсальности Lab широко используется способными в ней разобраться профессионалами.
Дата добавления: 2015-11-10 ; просмотров: 5920 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Урок 9
Кодирование рисунков
§ 12. Кодирование рисунков: растровый метод
§ 13. Кодирование рисунков: другие методы
Содержание урока
§ 12. Кодирование рисунков: растровый метод
Что такое растровое кодирование?
§ 13. Кодирование рисунков: другие методы
§ 12. Кодирование рисунков: растровый метод
Что такое растровое кодирование?
Ключевые слова:
• растр
• пиксель
• разрешение
• цветовая модель RGB
• цветовая модель CMYK
• цветовая модель HSB
• глубина цвета
• цветовая палитра
Рисунок состоит из линий и закрашенных областей. В идеале нам нужно закодировать все особенности этого изображения так, чтобы его можно было в точности восстановить из кода (например, распечатать на принтере).
И линия, и область состоят из бесконечного числа точек. Цвет каждой из этих точек нам нужно как-то закодировать. Так как точек бесконечно много, для этого нужно бесконечно много памяти, поэтому таким способом изображение закодировать не удастся. Однако «поточечную» идею всё-таки можно использовать.
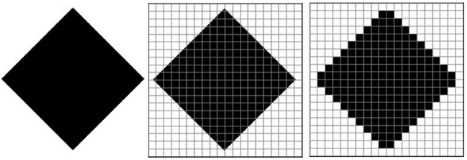
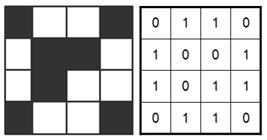
Начнём с чёрно-белого рисунка. Представим себе, что на изображение ромба наложена сетка, которая разбивает его на квадратики. Такая сетка называется растром. Теперь каждый квадратик внутри ромба зальём чёрным цветом, а каждый квадратик вне ромба — белым. Для тех квадратиков, в которых часть оказалась закрашена чёрным цветом, а часть — белым, выберем цвет в зависимости от того, какая часть (чёрная или белая) больше (рис. 2.19).
У нас получился растровый рисунок, состоящий из квадратиков-пикселей.

Разбив рисунок на квадратики, мы выполнили его дискретизацию. Действительно, у нас был непрерывный рисунок — изображение ромба. В результате мы получили дискретный объект — набор пикселей.
Двоичный код для чёрно-белого рисунка, полученного в результате дискретизации, можно построить следующим образом:
1) кодируем белые пиксели нулями, а чёрные — единицами 1) ;
2) выписываем строки полученной таблицы одну за другой.
1) Можно сделать и наоборот, чёрные пиксели обозначить нулями, а белые — единицами.
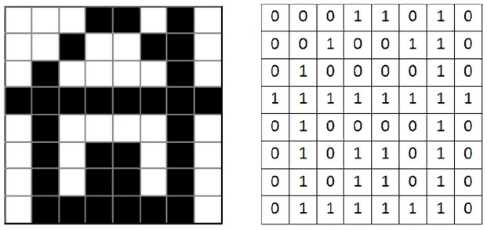
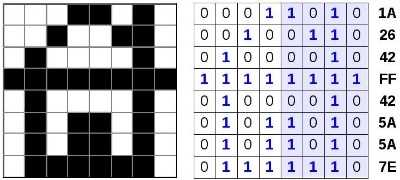
Покажем это на простом примере (рис. 2.20).
Ширина этого рисунка — 8 пикселей, поэтому каждая строка таблицы состоит из 8 двоичных разрядов — битов. Чтобы не писать очень длинную цепочку нулей и единиц, удобно использовать шестнадцатеричную систему счисления, закодировав 4 соседних бита (тетраду) одной шестнадцатеричной цифрой. Например, для первой строки получаем код 1А16:
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | A | ||||||
а для всего рисунка: 1A2642FF425A5A7E16.
Используя полученный шестнадцатеричный код картинки, подсчитайте её информационный объём в битах и байтах.
Очень важно понять, что мы приобрели и что потеряли в результате дискретизации. Самое главное — мы смогли закодировать изображение в двоичном коде. Однако при этом рисунок исказился — вместо ромба мы получили набор квадратиков. Причина искажения в том, что в некоторых квадратиках части исходного рисунка были закрашены разными цветами, а в закодированном изображении каждый пиксель обязательно имеет один цвет. Таким образом, часть исходной информации при кодировании была потеряна. Это проявится, например, при увеличении рисунка — квадратики увеличиваются и рисунок ещё больше искажается. Чтобы уменьшить потери информации, нужно уменьшать размер пикселя, т. е. увеличивать разрешение.

Разрешение обычно измеряется в пикселях на дюйм (используется английское обозначение ppi: — pixels per inch). Например, разрешение 254 ppi означает, что на дюйм приходится 254 пикселя.
Чем больше разрешение, тем точнее кодируется рисунок (меньше информации теряется), однако одновременно растёт и объём файла.
Одна и та же картинка была отсканирована дважды: в первый раз с разрешением 300 ppi, а второй раз — с разрешением 600 ppi. Что можно сказать о размерах полученных файлов?
Существуют два основных способа получения растровых изображений:
1) ввод с помощью какого-либо устройства, например сканера, цифрового фотоаппарата или веб-камеры; напомним, что при сканировании происходит преобразование информации в компьютерные данные (оцифровка);
2) создание рисунка с помощью какой-либо программы.
Используя дополнительные источники, найдите ответы на вопросы.
— Чему равен один дюйм в миллиметрах?
— Если отсканировать рисунок с разрешением 254 ppi, какой размер будет иметь изображение одного пикселя?
— Какие размеры в пикселях будет иметь изображение рисунка размером 10 х 15 см, если отсканировать его с разрешением 254 ppi?
Следующая страница 
Cкачать материалы урока
Декодирование JPEG для чайников
[FF D8]
Вам когда-нибудь хотелось узнать как устроен jpg-файл? Сейчас разберемся! Прогревайте ваш любимый компилятор и hex-редактор, будем декодировать это:
Специально взял рисунок поменьше. Это знакомый, но сильно пережатый favicon Гугла:
Последующее описание упрощено, и приведенная информация не полная, но зато потом будет легко понять спецификацию.
Даже не зная, как происходит кодирование, мы уже можем кое-что извлечь из файла.
[FF D8] — маркер начала. Он всегда находится в начале всех jpg-файлов.
Следом идут байты [FF FE]. Это маркер, означающий начало секции с комментарием. Следующие 2 байта [00 04] — длина секции (включая эти 2 байта). Значит в следующих двух [3A 29] — сам комментарий. Это коды символов «:» и «)», т.е. обычного смайлика. Вы можете увидеть его в первой строке правой части hex-редактора.
Немного теории
Закодированные данные располагаются поочередно, небольшими частями:
Каждый блок Yij, Cbij, Crij — это матрица коэффициентов ДКП (так же 8×8), закодированная кодами Хаффмана. В файле они располагаются в таком порядке: Y00Y10Y01Y11Cb00Cr00Y20.
Чтение файла
Файл поделен на секторы, предваряемые маркерами. Маркеры имеют длину 2 байта, причем первый байт [FF]. Почти все секторы хранят свою длину в следующих 2 байта после маркера. Для удобства подсветим маркеры:
Маркер [FF DB]: DQT — таблица квантования
Оставшимися 64-мя байтами нужно заполнить таблицу 8×8.
Приглядитесь, в каком порядке заполнены значения таблицы. Этот порядок называется zigzag order:
Маркер [FF C0]: SOF0 — Baseline DCT
Этот маркер называется SOF0, и означает, что изображение закодировано базовым методом. Он очень распространен. Но в интернете не менее популярен знакомый вам progressive-метод, когда сначала загружается изображение с низким разрешением, а потом и нормальная картинка. Это позволяет понять что там изображено, не дожидаясь полной загрузки. Спецификация определяет еще несколько, как мне кажется, не очень распространенных методов.
Находим Hmax=2 и Vmax=2. Канал i будет прорежен в Hmax/Hi раз по горизонтали и Vmax/Vi раз по вертикали.
Маркер [FF C4]: DHT (таблица Хаффмана)
Эта секция хранит коды и значения, полученные кодированием Хаффмана.
Следующие 16 значений:
Количество кодов означает количество кодов такой длины. Обратите внимание, что секция хранит только длины кодов, а не сами коды. Мы должны найти коды сами. Итак, у нас есть один код длины 1 и один — длины 2. Итого 2 кода, больше кодов в этой таблице нет.
С каждым кодом сопоставлено значение, в файле они перечислены следом. Значения однобайтовые, поэтому читаем 2 байта:
Далее в файле можно видеть еще 3 маркера [FF C4], я пропущу разбор соответствующих секций, он аналогичен вышеприведенному.
Построение дерева кодов Хаффмана
Мы должны построить бинарное дерево по таблице, которую мы получили в секции DHT. А уже по этому дереву мы узнаем каждый код. Значения добавляем в том порядке, в каком указаны в таблице. Алгоритм прост: в каком бы узле мы ни находились, всегда пытаемся добавить значение в левую ветвь. А если она занята, то в правую. А если и там нет места, то возвращаемся на уровень выше, и пробуем оттуда. Остановиться нужно на уровне равном длине кода. Левым ветвям соответствует значение 0, правым — 1.
Деревья для всех таблиц этого примера:
В кружках — значения кодов, под кружками — сами коды (поясню, что мы получили их, пройдя путь от вершины до каждого узла). Именно такими кодами закодировано само содержимое рисунка.
Маркер [FF DA]: SOS (Start of Scan)
Байт [DA] в маркере означает — «ДА! Наконец-то то мы перешли к финальной секции!». Однако секция символично называется SOS.
[00], [3F], [00] — Start of spectral or predictor selection, End of spectral selection, Successive approximation bit position. Эти значения используются только для прогрессивного режима, что выходит за рамки статьи.
Отсюда и до конца (маркера [FF D9]) закодированные данные.
Закодированные данные
Последующие значения нужно рассматривать как битовый поток. Первых 33 бит будет достаточно, чтобы построить первую таблицу коэффициентов:
Нахождение DC-коэффициента
1) Читаем последовательность битов (если встретим 2 байта [FF 00], то это не маркер, а просто байт [FF]). После каждого бита сдвигаемся по дереву Хаффмана (с соответствующим идентификатором) по ветви 0 или 1, в зависимости от прочитанного бита. Останавливаемся, если оказались в конечном узле.
2) Берем значение узла. Если оно равно 0, то коэффициент равен 0, записываем в таблицу и переходим к чтению других коэффициентов. В нашем случае — 02. Это значение — длина коэффициента в битах. Т. е. читаем следующие 2 бита, это и будет коэффициент:
Нахождение AC-коэффициентов
1) Аналогичен п. 1, нахождения DC коэффициента. Продолжаем читать последовательность:
2) Берем значение узла. Если оно равно 0, это означает, что оставшиеся значения матрицы нужно заполнить нулями. Дальше закодирована уже следующая матрица. В нашем случае значение узла: 0x31.
Читать AC-коэффициенты нужно пока не наткнемся на нулевое значение кода, либо пока не заполнится матрица.
В нашем случае мы получим:
Вы заметили, что значения заполнены в том же зигзагообразном порядке? Причина использования такого порядка простая — так как чем больше значения v и u, тем меньшей значимостью обладает коэффициент Svu в дискретно-косинусном преобразовании. Поэтому, при высоких степенях сжатия малозначащие коэффициенты обнуляют, тем самым уменьшая размер файла.
Аналогично получаем еще 3 матрицы Y-канала…
Но! Закодированные DC-коэффициенты — это не сами DC-коэффициенты, а их разности между коэффициентами предыдущей таблицы (того же канала)! Нужно поправить матрицы:
Теперь порядок. Это правило действует до конца файла.
… и по матрице для Cb и Cr:
Вычисления
Квантование
Вы помните, что матрица проходит этап квантования? Элементы матрицы нужно почленно перемножить с элементами матрицы квантования. Осталось выбрать нужную. Сначала мы просканировали первый канал. Он использует матрицу квантования 0 (у нас она первая из двух). Итак, после перемножения получаем 4 матрицы Y-канала:
… и по матрице для Cb и Cr.
Обратное дискретно-косинусное преобразование
Формула не должна доставить сложностей. Svu — наша полученная матрица коэффициентов. u — столбец, v — строка. Cx = 1/√2 для x = 0, а в остальных случаях = 1. syx — непосредственно значения каналов.
Приведу результат вычисления только первой матрицы канала Y (после обязательного округления):
Ко всем полученным значениям нужно прибавить по 128, а затем ограничить их диапазон от 0 до 255:
Например: 138 → 266 → 255, 92 → 220 → 220 и т. д.
YCbCr в RGB
4 матрицы Y, и по одной Cb и Cr, так как мы прореживали каналы и 4 пикселям Y соответствует по одному Cb и Cr. Поэтому вычислять так: YCbCrToRGB(Y[y,x], Cb[y/2, x/2], Cr[y/2, x/2]):
Вот полученные таблицы для каналов R, G, B для левого верхнего квадрата 8×8 нашего примера:
Конец
Вообще я не специалист по JPEG, поэтому вряд ли смогу ответить на все вопросы. Просто когда я писал свой декодер, мне часто приходилось сталкиваться с различными непонятными проблемами. И когда изображение выводилось некорректно, я не знал где допустил ошибку. Может неправильно проинтерпретировал биты, а может неправильно использовал ДКП. Очень не хватало пошагового примера, поэтому, надеюсь, эта статья поможет при написании декодера. Думаю, она покрывает описание базового метода, но все-равно нельзя обойтись только ей. Предлагаю вам ссылки, которые помогли мне: