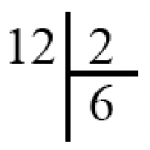как перевести число в бинарный код
Как проводится перевод числа из десятичной системы в двоичную?
Содержание:
Перевод из десятичной в двоичную систему исчисления проводится несложно. Для этого действия есть собственный специализированный алгоритм, который мы рассмотрим чуть ниже.
Перевод из десятичной в двоичную систему: целые числа
Пример, как осуществляется перевод из десятичной в двоичную систему
Перевод из десятичной в двоичную систему: дробные числа
Здесь тоже не все может быть сразу понятно, но взглянув на пример, все сразу станет ясно.
Пример, как осуществляется перевод дробного десятичного числа в двоичную систему
Эту конвертацию можно осуществлять до того момента, пока мы не добьемся нужного уровня погрешности. Но для демонстрации алгоритма конвертации этого достаточно. В результате мы получили, что десятичное число 0,234 в двоичном исчислении будет равняться 0011101111100.
А как конвертировать дробное число, если у него в целой части будет какое-то другое значение, кроме 0? Например нам нужно конвертировать число 10,25. В этом случае целая и дробная части будут переводиться раздельно:
Вот что мы получим по факту:
В конце наших вычислений мы получим, что десятичное число 10,25 в двоичной форме будет выглядеть вот так — 1010,01. Кстати, если внимательно посмотреть, то видно, что при конвертации в двоичную форму дробной части нашего примера (при умножении на 2), дробная часть стала равняться 0, поэтому вычисления закончились.
Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
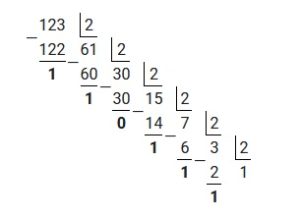
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
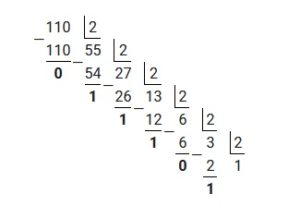
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Двоичная система счисления: как переводить, как реализовать на C и C#
Что такое двоичная система счисления?
Это такая бинарная система счисления (бинарная, потому что у неё имеется лишь два основания, т. е. две цифры – “0” и “1”), которая используется в самой основе компьютера, так как в компьютерных схемах, процессорах, платах имеются, так называемые, выключатели (или биты). Если на какой-либо схеме выключатель поставлен в позицию выкл., то ему соответствует цифра “0”, если вкл. – “1”. Благодаря таким вот массовым чередованиям позиций вкл\выкл и соответствующим им единиц и нулей и работают абсолютно все компьютеры.
Последовательность этих цифр, приводящая к каким-либо результатам в работе компьютера, называется машинным кодом – это самый сложный и самый низкий язык программирования, но раньше люди умудрялись программировать и на нём. Сейчас же эти коды обрамляются в более легкие и понятные ключевые слова, и формы, которые в последствии составляют различные языки программирования. Абсолютно все языки программирования в своей основе имеют под собой работу машинного кода, любая функция, любой оператор, любой метод записан в машинном коде в виде огромной последовательности единиц и нулей. Любой printf в С или Console.WriteLine обязательно разлагаются для компьютера на машинный код, только так он и может понять, что мы от него хотим.
Переводом исходного кода какого-либо языка программирования в машинный код занимается компилятор.
Алгоритм перевода в двоичную систему счисления из десятеричной.
Теперь рассмотрим алгоритм перевода каких-либо чисел из стандартной, десятеричной системы счисления в двоичную.
Итак, например, у нас имеется число 12 в десятеричной системе счисления, давайте переведем его в двоичную. Можно сделать это несколькими формами записи, кому как удобно.
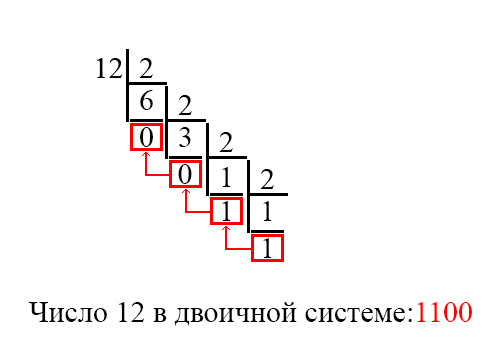
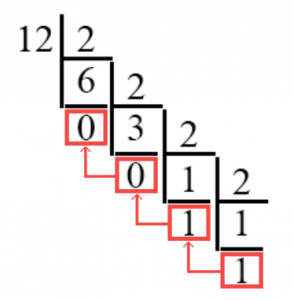
Рассмотрим первый вариант. Он будет похож на несколько видоизменённое деление в столбик, и выглядеть будет вот так:
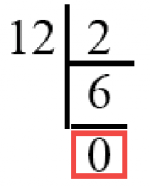
Теперь разберём, что тут написано. Сначала мы, как и в делении в столбик, пишем число, которое мы хотим делить (12), и число, на которое делим (в двоичной системе счисления это всегда 2).
12, делённое на 2 без остатка будет равно 6. Записываем это как положено в делении в столбик.
Итак, теперь стоит сказать самое главное о переводе чисел из десятичной системы счисления в двоичную: если число делится на двойку без остатка, то мы пишем ноль, если с остатком – единицу.
Рассмотрим это правило поподробнее. Мы уже сказали, что 12 / 2 =6. Остатка у нас нет. Значит мы пишем ноль. В данном методе разбора мы пишем его под цифрой 6.
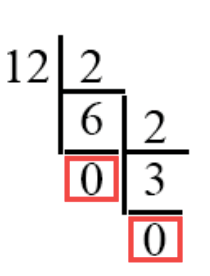
Кусочек двоичного кода мы уже получили. Вычисляем дальше.
Теперь мы делим 6 на 2. Получается 3, и опять деление прошло без остатка – опять мы пишем, уже под тройкой, ноль.
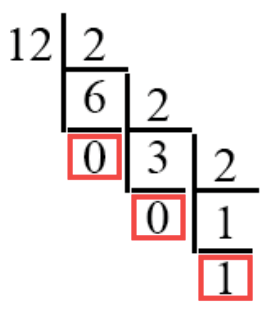
Теперь делим 3 на 2. На этот раз мы понимаем, что получается ответ с остатком – 1 и 0.5. Если происходит такое, то мы откидываем полученный остаток и делим полученное число без остатка на два, при этом подписываем ниже единицу.
Далее нам стоит запомнить, что мы всегда делим последнюю единицу на два. Всегда после того или иного вычисления двоичного числа у нас так или иначе в итоге получается число 1 (как на примере, при делении 3 на 2). И абсолютно всегда мы его делим на 2. И абсолютно всегда последней цифрой в последовательности наших нулей и единиц будет цифра 1, так как все числа в двоичной системе счисления начинаются с единицы (исключение – 0, в двоичной системе счисление он и будет записан как 0).
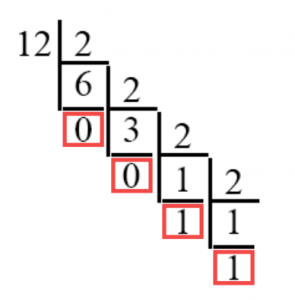
Поэтому мы считаем нашу последовательность “с конца”, и у нас получается число 1100. Это и есть ответ.
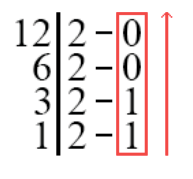
Теперь давайте рассмотрим вторую форму записи такого деления. Она менее громоздка, но по сути является той же самой формой деления.
Здесь мы просто делим получаемые числа на два через черту, и, если частное получается без остатка, через тире пишем 0, если с остатком – 1. Опять же не забываем округлять числа с остатком в меньшую сторону, делить последнюю единицу на двойку и считывать последовательность в обратном порядке.
Реализация перевода числа из десятичной системы счисления в двоичную на языке C#
Как быстро переводить из десятичной системы в двоичную
Бинарный код имеет огромное значение в информатике. При помощи него в ЭВМ представляются данные и производятся вычисления. Именно поэтому тем, кто решил связать свою жизнь с компьютерными технологиями следует с ним разобраться. В этой статье рассмотрим, как переводить в двоичную систему числа. Многим кажется это сложным, однако это очень просто – проблем не возникнет даже у чайников. Также тут присутствует тренажер, который поможет вам закрепить материал.
Основные определения
Перед тем как переходить к сути вопроса, необходимо знать всего лишь одно основное положение. А именно, что представляет собой бинарная система исчисления.
Двоичная система — позиционное счисление с основанием два. В качестве алфавита здесь используются всего лишь два символа (цифры) 0 и 1.
Слово позиционное значит, что цифра меняет свое значение в зависимости от её положения в числе. Чтобы у вас сформировалось представление, приведем в пример десятичную нумерацию, где используются цифры от 0 до 9. Возьмите 1 и 100, здесь в первом случае единица обозначает один, а во втором уже 100. Это все что вам нужно знать, перейдем к практике.
Как переводить в двоичную систему счисления
Хочу вас обрадовать – сложных формул тут не будет. Если вы умеете делить, складывать и вычитать столбиком, то больше никаких знаний получать не нужно. Этого вам вполне хватит, чтобы усвоить информацию представленную ниже. Также нам придется запастись специальной таблицей значений. Вот такую таблицу я нашел в интернете. Она понадобится вам на первое время для самопроверки.
Правила и полезные свойства
Рассмотрим несколько простых свойств, которые помогут вам быстро переводить величины в двоичную нумерацию.
Метод счета поможет перевести небольшие величины. Смотрите, в десятичном формате, используя все знаки от 0 до 9 мы, добавляем разряд (нолик в конец записи). Это касается и двоичной формы отображения. Однако, знаков здесь всего два – нуль и единичка. Вот как это выглядит:
При переполнении разряда также добавляется новый.
Перевести величины вам поможет еще одна полезная особенность. Добавляя нуль в конце, мы увеличиваем значение в два раза. Если не верите, то проверьте по таблице.
На этом здесь можно закончить. Теперь перейдем к основному алгоритму, с помощью которого можно перевести в двоичное счисление.
Как переводить числа – алгоритм
Чтобы переводить значения, вы должны знать, как делить столбиком. Способ очень простой — вам всего лишь нужно делить величину на 2 до тех пор, пока не получите остаток меньше основания СС (меньше двойки). После чего записывают результат снизу вверх. Многим нравится выполнять эту операцию столбиком. Например, возьмем 17:
Однако мне так записывать вычисление не нравится. Я предпочитаю такую форму записи:
Суть точно такая же. Однако, как по мне, в представленной выше записи сложнее запутаться, так как меньше знаков нужно хранить в уме, да и выглядит решение куда как короче и нагляднее. Какой из двух предложенных вариантов выбрать решать только вам.
Обладая этой информацией, вы сможете перевести в бинарный код всё, что вам нужно. Для закрепления материала ниже представлен специальный тренажер для перевода величин в различные счисления. Помните, что усвоение теории зависит того сколько времени вы потратите на практику.
Тренажер, чтобы научиться переводить числа в различные сс
Введите значение
Сгенерировать случайное
Выбрать основание СС
Заключение
Вот и все, вы научились, как переводить в двоичную систему счисления числа из десятичной нумерации. Как видно выполнять перевод несложно – справится даже младшеклассник. Ну а как вы усвоите знания зависит только от того сколько времени вы уделите практике. Если что-то перевести у вас так и не получилось, то пишите в комментарии, и мы постараемся вам помочь.