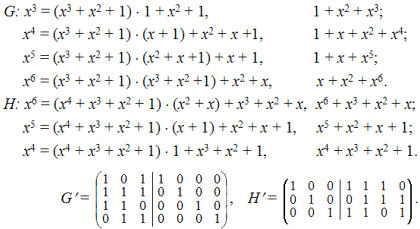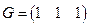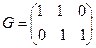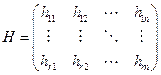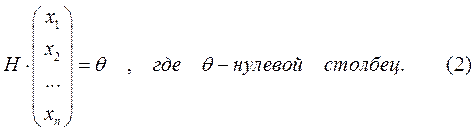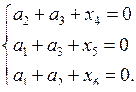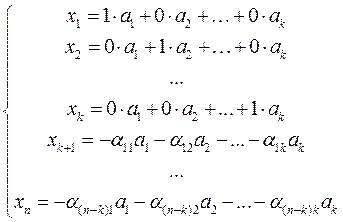как найти порождающую матрицу кода
Как найти порождающую матрицу кода
Откуда же берутся порождающие матрицы G? Порождающая матрица получается путем последовательного сдвига соответствующего порождающего многочлена g(x) по разрядам вправо. Последовательному сдвигу вправо отвечает умножение g(x) на x i :
G = 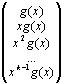
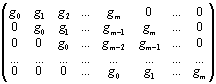
причем x n + 1 = g(x)h(x), где, напомним, n — общее число символов, k — число информационных, а m — число проверочных символов в кодовом слове. Если существует порождающая матрица G, то должна существовать и соответствующая ей проверочная матрица H. Действительно, такую матрицу можно получить путем последовательного сдвига проверочного многочлена h(x) влево:
H = 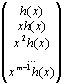
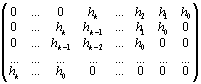
G = 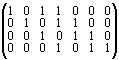
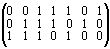
Последнее равенство говорит о том, что матрицы G и H ортогональны относительно друг друга (звездочка означает операцию транспонирования матрицы).
Рассмотренные G и H матрицы называются ленточными, потому что нули и единицы вдоль обеих диагоналей этих матриц образуют своеобразные ленты. Но любая ленточная матрица может быть сведена к систематическому виду:
Существует, по крайней мере, два способа сведения ленточных матриц к систематическому виду. Первый наиболее надежный способ состоит в нахождении ряда остаточных многочленов. Если ri(x) остаточный многочлен от деления xi на порождающий многочлен g(x), то сумма элементов ri (x) + xi дает строки систематической матрицы G. Аналогичным способом находятся строки проверочной матрицы H. Второй способ заключается в том, чтобы найти соответствующие линейные комбинации строк или столбцов исходных матриц ленточного типа. Найдем G и H для предыдущего случая:
Эти две систематические матрицы можно было бы получить путем сложения векторов-столбцов исходных ленточных матриц (напоминаем, счет столбцов для G матрицы начинается с нуля, а для H матрицы — с шести).
G’ : 0′ = 1 + 2, 1′ = 1 + 5, 2′ = 3, 3′ = 0, 4′ = 1, 5′ = 4 + 1, 6′ = 6;
H’ : 0′ = 5, 1′ = 3, 2′ = 4, 3′ = 2, 4′ = 6, 5′ = 1, 6′ = 0.
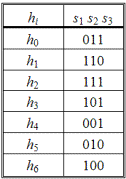
Теперь поясним, как составить проверочные соотношения и определить коды ошибок si по известной проверочной матрице. С этой целью выпишем три равенства, отвечающих строкам матрицы H’ :
При ошибке в символе h0 суммы s2 и s3 изменятся на 1, а при ошибке в h1 не будут равны нулю суммы s1 и s2. Таким образом, можно составить все коды ошибок для всех символов (табл. 2.87).
При одновременном появлении ошибок в двух символах, например в h5 и h6, коды ошибок будут складываться; в данном случае он становится таким же, как и при одиночной ошибке в символе h1. Поэтому, характеризуя код с точки зрения помехозащищенности, мы должны сказать, что он обнаруживает и исправляет любые одиночные ошибки, а также обнаруживает, но не исправляет двойные ошибки.
Задание линейных кодов с помощью порождающих и проверочных матриц
Линейные коды задаются с помощью порождающей G(x) и проверочной H(x) матриц. Эти матрицы связаны основным уравнением кодирования:
Матрица G(x) содержит k строк и n столбцов, ее элементами являются нули и единицы. В качестве строк матрицы G(x) выбираются любые ненулевые линейно независимые n-значные векторы, отстоящие друг от друга не менее чем на заданное кодовое расстояние d0.
Векторы v1, v2, …, vk называются линейно независимыми, если выполняется условие
где сi=<0, 1>, а сложение выполняется по модулю два. То есть, каким бы образом мы не суммировали различные строки матрицы G(x), не получим суммы, равной нулю. Все множество кодовых слов состоит из строк порождающей матрицы и всевозможных комбинаций этих строк, т.е. суммы по модулю два всех строк матрицы G(x) сначала попарно, затем по три и так далее до суммы всех k строк.
С точки зрения алгебры все кодовые слова образуют некоторое векторное пространство, базисом которого являются строки матрицы G(x).
Поскольку линейно независимые векторы могут быть выбраны произвольным образом, то, очевидно, можно построить множество матриц G(x) с одним и тем же кодовым расстоянием d0.
Свойство линейной независимости векторов инвариантно относительно двух следующих операций (выполняя эти две операции, кодовое расстояние не меняется):
1) возможна произвольная перестановка строк и столбцов в матрице G(x);
2) замена i-й строки на сумму i-й и j-й строк и т. д. (эту операцию нельзя осуществлять со столбцами матрицы G(x)).
Производя вышеуказанные операции, любую произвольную матрицу G(x) можно привести к так называемому приведенно-ступенчатому (каноническому) виду:
где Ik –единичная подматрица размерностью k×k,
H * T – транспонированная проверочная матрица (транспонировать – значит поменять местами строки и столбцы).
Исходя из основного уравнения кодирования, проверочная матрица имеет вид
Возьмем порождающую матрицу кода (7,4). В этой матрице количество строк равно 4 (k=4), а количество столбцов 7(n=7).
Для того чтобы построить проверочную матрицу, необходимо транспонировать подматрицу G(x) * и к ней приписать единичную матрицу размером l×l. Проверочная матрица будет иметь размер l×n, l = n-k=7-4=3, т.е. матрица Н(x) имеет размер 3×7.
Порождающая и проверочная матрицы
Порождающей матрицей линейного 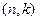
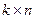
является порождающей матрицей кода из двух слов <000, 011>.
является порождающей для кода В из примера 6.3.
Мы знаем, что кодовые слова – линейные комбинации базисных векторов, т.е. строк матрицы 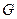
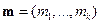
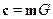
Тем самым вектор из 
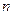
Обратимся к задаче декодирования.
Предположим, что для некоторого двоичного вектора 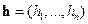
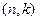
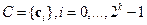
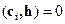

в котором 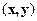
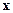
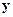
Про такой вектор 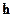
Заметим, что (6.2) справедливо для всех кодовых слов, если оно справедливо для базисных векторов, т.е. если
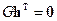
где верхний индекс Т обозначает транспонирование.
Чем больше таких «проверок» мы найдем, тем, по-видимому, больше ошибок сумеем обнаружить и исправить.
Упражнение 6.4. Докажите, что проверки образуют линейное пространство.
Это пространство назовем пространством, ортогональным линейному коду или проверочным пространством.
Упражнение 6.5. Найдите размерность линейного пространства проверок.
Чтобы выполнить последнее упражнение, нужно заметить, что в матрице 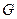

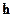
Следствием этих рассуждений является теорема
Теорема.Размерность проверочного пространства линейного 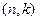
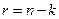
Базис проверочного пространства запишем в виде матрицы
называемой проверочной матрицей кода.
Проверочная и порождающая матрицы связаны соотношением
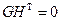
Из этого соотношения мы видим, что для любого кодового слова 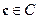
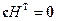
Это тождество можно использовать как критерий принадлежности произвольной последовательности коду, т.е. для обнаружения ошибок.
Зная, 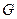
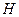
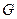
Перестановка столбцов матрицы 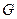
Понятно, что для каждого кода найдется эквивалентный, для которого первые 

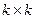
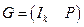
где 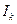

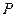
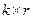
Матрица вида (6.6) называется порождающей матрицей, приведенной к систематическому виду, а соответствующий код называется систематическим. Кодирование для систематического кода немного проще, чем для кода общего вида:
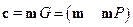
т.е. в кодовом слове первые 
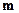
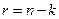
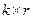
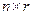
Для систематического кода с порождающей матрицей в форме (6.6) проверочная матрица может быть вычислена по формуле
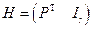

Как найти проверочную матрицу для несистематического кода?
Очень просто. Нужно привести матрицу к систематическому виду и воспользоваться (6.7). Если первые 

Упражнение 6.7.Сформулируйте алгоритм нахождения порождающей матрицы по проверочной.
Упражнение 6.8.Объясните, почему любой набор номеров 
Упражнение 6.9.Постройте порождающие и проверочные матрицы для кодов из примера 6.4.
Подведем итоги этого важного параграфа.
Линейный 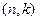
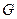
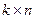
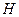
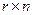
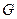
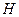
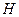
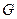
Матрица 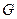
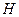
Проверочная матрица линейного кода
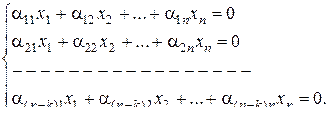
Матрица H=(aij) коэффициентов системы (1) называется проверочной матрицей линейного (n, k) кода и однозначно определяет множество кодовых векторов, являющееся правым нуль-пространством матрицы H. Код называется систематическим, если первые k символов являются информационными: 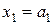
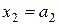
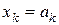
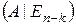
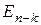
Систему (1) можно переписать в матричном виде:
Пример 1. Пусть q = 2, n = 6, k = 3, H = 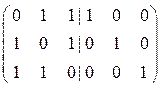
Сообщение (а1 а 2 а3) кодируется вектором х = (а1 а2 а3 х4 х5 х6), то есть 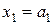
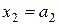
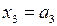
Имеем систему уравнений:
Если передано сообщение а = 011, то соответствующим кодовым вектором будет х = 011011. Всего имеется 2 3 кодовых векторов:
000000, 011011, 110110, 001110,
100011, 111000, 010101, 101101.
Порождающая матрица линейного кода
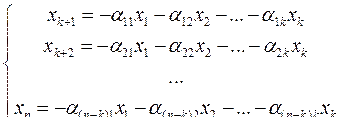
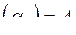
Перепишем в матричном виде:
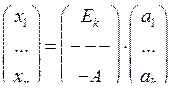
Свойства порождающей матрицы:
1. Все кодовые слова можно получить, умножая информационный вектор на матрицу G.
(a1, a2, …, ak) ∙ G = (x1, x2, …, xn) 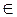
2. Строки матрицы G являются кодовыми словами.
Пусть 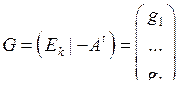
3. Любая линейная комбинация строк матрицы G является кодовым словом, и наоборот.
4. Строки матрицы G линейно независимы.
Так как в начале матрицы G стоит единичная матрица, то её строки образуют ступенчатую систему, а значит, g1, g2,…, gk линейно независимы. Из свойств 3 и 4 следует свойство 5.
5. Строки матрицы G g1, g2,…, gk образуют базис линейного пространства кода С.
Пример 2. Дана проверочная матрица 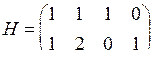
Скорость передачи данного кода k/n = 2/4 = ½
Матрица H имеет вид: H = 
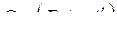
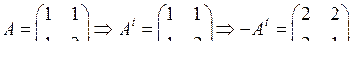
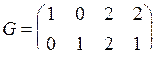
Составим таблицу кодирования. Всего может быть 9 различных информационных сообщений (a1,a2): 00, 01, 02, 10, 11, 12, 20, 21, 22. Они записаны в первых двух столбцах таблицы. Соответствующие им кодовые векторы находим, умножая информационное сообщение на матрицу G:
(a1 a2) ∙ 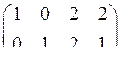
Аналогичные результаты можно получить, записав систему проверочных уравнений, определяемую матрицей Н, и учитывая, что 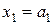
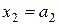
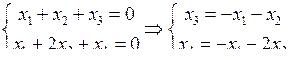
В качестве порождающей матрицы этого же кода можно взять матрицу G= 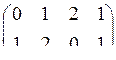
Дата добавления: 2019-02-12 ; просмотров: 1210 ; Мы поможем в написании вашей работы!