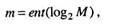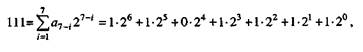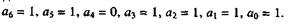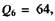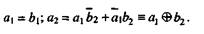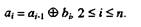к характеристикам кода относятся

Характеристики кодов

Код характеризуется следующими основными параметрами:

— длина кодовой комбинации (n)

— число кодовых комбинаций(N)

Длина кодовой комбинации п (значность кода) равна количеству составляющих ее элементов п.

Число кодовых комбинаций N определяется как N =m n

Если длина всех кодовых комбинаций одинакова, то код назы­вается равномерным, в противном случае – неравномерным.

Таким образом, равномерные коды составляют класс блоковых кодов, в которых каждому отдельному знаку сообщения сопоставля­ется кодовая комбинация (блок) из определенного числа элементар­ных символов.

В простом равномерном коде число разрядов в кодовой комби­нации зависит от объема исходного алфавита и основания кода. Не­обходимая длина кодовой комбинации определяется как п= log_mN.

Так, если необходимо передать 32 (N = 32) буквы русского ал­фавита или 26 букв латинского алфавита, то п= log₂32 =5.

Любая из пятиэлементных комбинаций представляет собой ка­кой-либо знак исходного алфавита. Если в процессе передачи такой кодовой комбинации произойдет одна или несколько ошибок, то принятая кодовая комбинация будет интерпретироваться приемни­ком как кодовая комбинация, соответствующая другому знаку. По­скольку все возможные кодовые комбинации простого кода задействуются для передачи информации, то все они являются разрешен­ными для передачи информации или просто разрешенными, и появ­ление ошибки в одной разрешенной комбинации переводит ее в дру­гую, также разрешенную.

Коды, у которых все кодовые комбинации являются разрешен­ными, называются простыми или равнодоступными.

Обнаружить ошибку при приеме может только получатель и только в случае, если передается смысловое сообщение, само по се­бе обладающее избыточностью.

В системах передачи информации широко используются про­стые, двоичные, равномерные коды с n=5, 6, 7, 8.

Источник

Параметры и характеристики кодов

В процессе кодирования элементы передаваемого сообщения преобразуются в соответствующие им числа (кодовые символы). Каждый элемент записывается определенной совокупностью кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, отражающих дискретные сообщения, представляет собой код. Правило кодирования можно выразить различным образом. Наиболее удобна кодовая таблица, где приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество т — основанием кода. Число разрядов 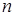, образующих кодовую комбинацию, называется разрядностью кода или длиной кодовой комбинации. К основным параметрам кодов относятся также расстояние между кодовыми комбинациями и вес кодовой комбинации

. Расстояние характеризует различие между двумя кодовыми комбинациями и определяется числом несовпадающих в них разрядов, а именно числом единиц в сумме двух комбинаций «по модулю 2». Число ненулевых элементов в кодовой комбинации определяет ее вес .

По длине кодов и взаимному расположению в них символовразличают равномерные и неравномерные коды.

Для передачи данных по каналам связи рекомендован семиэлементный код МТК-5, известный также как код ASCII – стандартный американский код для обмена информации, где число возможных комбинаций составляет уже . В настоящее время код ASCII расширен до восьми двоичных разрядов и число кодовых комбинаций возросло до 256, что позволило использовать этот код для кодировании сообщений на многих языках мира.

Коды МТК-2 и МТК-5 являются первичными (простыми). Применение равномерных кодов упрощает построение буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.

Неравномерные коды отличаются тем, что кодовые комбинации у них отличаются друг от друга не только взаимным расположением символов, но и их количеством при минимизации средней длины кодовой последовательности. Это приводит к тому, что различные комбинации имеют различную длительность.

По признаку помехозащищенности коды, как и методы кодирования, делятся на примитивные (первичные, простые, безызбыточные) и помехоустойчивые (корректирующие, избыточные).

Коды, у которых все возможные кодовые комбинации используются для пе­редачи информации, называются примитивными или кодами без избыточно­сти. В простых равномерных кодах превращение одного символа комбинации в другой, например 0 в 1 или 1 в 0, приводит к появлению новой разрешенной комбинации, т. е. к ошибке в принятом сообщении. Примитивное, или безызбыточное, кодированиеобычно применяется для согласова­ния алфавита источника и алфавита канала.

В помехоустойчивых кодах (избыточных) для передачи сообщения используются не все кодовые комбинации, а только некоторая их часть (разрешенные кодовые комбинации). Другая часть кодовых комбинаций используется для обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов.

Различают помехоустойчивые коды с обнаружением и исправлением ошибок. Код с обнаружением ошибок уменьшает число неверно опознанных сообщений, позволяет «стирать» или особо отмечать сообщения, в которых установлено присутствие ошибки, а в некоторых случаях (системы с обратными информационными связями) принять меры к повторной передаче и приему неопознанных сообщений.

Простейшим из помехоустойчивых кодов является код с проверкой на четность. Этот код позволяет обнаруживать одиночную ошибку. Его суть за­ключается в следующем. На передающем конце канала связи устройство ко­дирования проводит подсчет числа логических «1» в передаваемом двоичном кодовом слове. Если сумма «1» оказывается нечетной, в конец передаваемой кодовой комбинации добавляется «1», а если нет, то «0». На приёмном конце канала связи проводится аналогичный подсчет, и, если контрольная сумма (число единиц в принятой кодовой комбинации) будет нечетной, то принимается решение о том, что при передаче произошло искажение информации, в противном случае принятая информация признается достоверной. При контроле на четность единственный способ получить достоверную информацию — повторная передача кодового слова. Для этого приемник формирует специальную команду, которая передается по каналу связи в обратном направлении к передатчику сообщения.

Построение кодов с обнаружением ошибки можно провести так, что для кодирования используются только те кодовые комбинации, которые отличаются друг от друга на два символа (избыточный код), а остальные кодовые комбинации запрещены. Появление запрещенной кодовой комбинации позволяет обнаружить ошибку. Пусть мы имеем трехразрядный код, из которого можно составить кодо- вые комбинации 000; 001; 010; 011; 100; 101; 110 и 111. Для обнаружения ошибки выберем комбинации, отличающиеся на два символа: 000; 011; 101 и 110. При наличии ошибки, т.е при появлении в одном из разрядов вместо нуля единицы или наоборот, мы получим запрещенный код, что говорит о наличии ошибки.

Рассмотрим код, исправляющий одиночную ошибку. Общий принцип построения такого кода аналогичен принципу построения кода, обнаружи-вающего одиночную ошибку. Однако, в этом случае, чтобы исправить одну ошибку, все отобранные кодовые слова должны отличаться друг от друга как минимум на три символа. Одиночная ошибка переведет переданное слово в одно из запре­щенных, что и позволит обнаружить ошибку, но полученное запрещенное слово отличается от переданного лишь одним символом, а от остальных разрешенных слов — не менее чем на два символа. Значит принятое слово «ближе» к действительно переданному и менее похоже на остальные разрешенные слова. Поэтому, в качестве переданного слова принимается то из разрешенных, которое отличается от принятого на меньшее число символов, что позволяет исправить одиночную ошибку.

Обратим внимание на то, что практически пока не существует кодов, позволяющих обнаруживать и тем более исправлять все возможные ошибки. Можно построить лишь коды, обнаруживающие или исправляющие некоторое число ошибок определенного вида. Естественно, что в таком случае необходимо заботиться об обнаружении и исправлении наиболее вероятных или опасных ошибок.

В настоящее время разработано большое количество кодов и методов кодирования источников сообщений. Многие из них реализованы на практике, особенно для сжатия сообщений с большой избыточностью, например факсимильных, телевизионных и другой видеоинформации, где они позволяют увеличить скорость передачи сообщений в сотни раз.

Устройства, осуществляющие кодирование, принято называть кодерами. После процесса кодирования кодовые сигналы модулируются для преобразования этих символов в сигналы, пригодные для передачи по каналам связи. При непосредственной передаче кодированного сигнала переносчиком может быть и постоянный ток, изменяющимися параметрами которого являются амплитуда и направление тока. Однако в качестве переносчика чаще используется гармоническое или импульсное колебания, при котором можно получить различные виды модуляции (см.разделы 9-14).

Источник

Основные понятия и определения. Классификация кодов и их основные параметры

Квантованный АИМ-2 сигнал, в принципе, можно считать кодовым с основанием кода, равным числу М разрешенных уровней (уровней кван­тования) и с числом символов в кодовой группе, равным единице. Таким образом, квантованный сигнал является многоуровневым.

Многоуровневые сигналы весьма неудобны для передачи, так как при­емник должен различать все разрешенные уровни. Кроме того, такие сиг­налы трудно восстановить (регенерировать), если они подверглись воз­действию помех. Иными словами, многоуровневым сигналам в большой степени свойственны недостатки аналоговых сигналов. Поэтому в ЦСП обычно используются коды со сравнительно малым основанием, чаще всего двоичные. Процесс преобразования многоуровневого сигнала в код с низким основанием называется кодированием. Результатом кодирования является комбинация символов (посылок, цифр), представляющая в соот­ветствующей системе счисления номер разрешенного уровня квантован­ного сигнала. В ЦСП с ИКМ-ВРК широкое применение нашла двоичная система счисления. Запись любого квантованного уровня с М разрешен­ными уровнями в двоичной системе счисления может быть представлена в виде

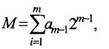Поскольку выбор числа уровней квантования определяется допусти­мой величиной шага квантования, обычно приходится решать обратную задачу: определение минимально необходимого числа разрядов кода, ко­торый может быть использован для кодирования при заданном М. Оче­видно, что для двоичного кода имеем

здесь ent означает большее целое число от выражения в круглых скобках.

Пример. Требуется определить необходимое число разрядов дво­ичного кода для кодирования числа 111 и записать его двоичным кодом.

Решение. Необходимое число разрядов согласно (9.64) будет рав­но: 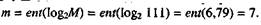Запись числа 111 соглас­но (1.63) будет иметь вид

т.е. ему соответствует кодовая комбинация 1101111 со следующими наче-ниями разрядных цифр:

Набор величинможно рассматривать как ряд эталонных сигна-

лов с определенным 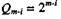номером разряда. Для нашего примера

Однозначная связь величи­ныэталонного сигнала с номером разряда двоичного эквивалента раз­решенного квантованного уровня позволяет ограничиться передачей только ряда величин а„ составляющих кодовую комбинацию (или кодо­вую группу).

Множество используемых кодовых комбинаций, связанных единым законом построения, называется кодом. Простейшим кодом является код, в основе построения которого лежит отношение (1.63) и называется на­туральным двоичным кодом.

Графически коды удобно изображать кодовыми таблицами или ко­довыми растрами, характеризующими связь уровней квантования и соответствующих им кодовых комбинаций, представляя их по порядку уровней. Кодовые таблицы наиболее широко применяемых в ЦСП ко­дов приведены на рис. 1.23

Перестановка порядка следования кодовых комбинаций на обратный дает простой обратный код, веса разрядов которого показаны внизу. На­пример, уровень М = 11 в натуральном коде представляется кодовой ком­бинацией вида 1011 (см. рис. 1.23,а), обратный код будет иметь вид 1101.

Замена всех импульсов в кодовой комбинации на пробелы (или единиц на нули, а нулей на единицы) приводит к инверсному коду. Так, например, для М = 11 кодовая комбинация в инверсном коде имеет вид 0100. Другим типом кода, применяемого в ЦСП, является код Грея (он же рефлексный или зеркальный). Его отличительной особенностью является то, что лю­бые две соседние кодовые комбинации отличаются друг от друга лишь в одном разряде (рис. 1.23,6). Код Грея находит применение при кодирова­нии групповых телефонных и широкополосных телевизионных сигналов, для которых различие символов в большом числе разрядов кодовых групп соседних уровней квантования нежелательно, так как в этих случаях ошибки кодирования и декодирования особенно опасны. Но код Грея не

так легко декодировать. Поэтому его обычно преобразуют в натуральный двоичный код, декодирование которого особых трудностей не представ­ляет. Правило формирования кода Грея следующее: первые разряды оп­ределяют точно 2′ блоков смежных уровней, разделенных посредством 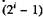порогов, а i-й разряд обозначает переход от единицы к нулю или наоборот на всех порогах, которые еще не определены переходами пре­дыдущих разрядов.

Преобразование кода Грея в натуральный двоичный код осуществля­ется следующим образом.

Если обозначить разряды двоичного натурального кода через а\. а_п, а разряды кода Грея через 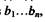то

Символ Ф в правой части последнего выражения означает сложение по модулю 2, а эта операция тождественна логической функции исключи­тельное ИЛИ, представленной в средней части последнего выражения, аналогичное правило распространяется на все последующие разряды, а именно:

Сравнение таблиц натурального двоичного кода и кода Грея подсказы­вает довольно простое правило преобразования кода Грея в натуральный: в i-м разряде натурального кода формируется импульс или пробел в зави­симости от того, нечетным или четным было число импульсов в преды­дущих импульсных позициях комбинации кода Грея (включая i-ю пози­цию). Например, комбинации 1011001 кода Грея соответствует согласно этому правилу комбинация 1101110 натурального кода. Операция опреде­ления четности или нечетности числа импульсов может быть выполнена при помощи триггера.

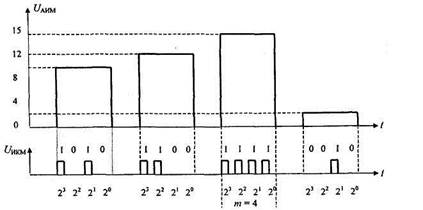
Рис. 1.24. Процесс кодирования отсчетов t/дим в кодовые комбинации

На рис. 1.24 приведены временные диаграммы, поясняющие процесс кодирования квантованного группового АИМ сигнала при использовании четырехразрядного натурального двоичного кода.

. Амплитуды отсчетов, поступающие на вход кодирующего устройства (кодера), принимают значения в диапазоне £/дим = 0. 15 условных шагов квантования, а на выходе кодера формируется цифровой сигнал £/икм. представляющий последовательность четырехразрядных кодовых комби­наций. Последовательность /и-разрядных кодовых комбинаций на выходе кодера представляет собой групповой сигнал с импульсно-кодовой моду­ляцией, называемый цифровым.

Основными характеристиками кодов являются:

— избыточность кода, под которой понимается отношение максимально
возможного числа кодовых комбинаций при данной разрядности кода к
числу фактически используемых комбинаций. Код, в котором используется
весь ансамбль комбинаций (рис. 1.23), является неизбыточным;

— возможность обнаружения ошибок, т.е. по изменению структуры
кодовой комбинации можно судить о наличии ошибок. Для кода с посто­
янной диспаритетностью при искажении одного из разрядов кодовой ком­
бинации происходит изменение диспаритетности, что приводит к появле­
нию на приеме кодовой комбинации, не входящей в ансамбль используе­
мых кодовых комбинаций, что говорит о наличии ошибки. Если в 7-
разрядной кодовой комбинации имеется 4 единицы и 3 нуля, то любая
одиночная ошибка приводит к нечетному числу единиц. Поэтому, чтобы
убедиться, произошла или нет подобная ошибка, необходимо определить
нечетное или четное число принятых единиц. Этот метод носит название
проверки на четность;

— возможность исправления ошибок, т.е. по изменению структуры ко­
довой комбинации и кодового расстояния между соответствующими кодо­
выми комбинациями не только обнаруживается ошибка, но и устраняется.

Источник

6.7. Основные характеристики кодов

Оценка кодов обычно производится по их основным характеристикам, выражающим различные количественные и качественные показатели. Данные ха­рактеристики используются при выборе кодов, предна­значенных для передачи, хранения и обработки инфор­мации: длина кода; основание кода; мощность кода; полное число кодовых комбинаций. число информационных символов; число проверочных символов; избыточность кода; скорость передачи; вес кодовой комбинации; кодовое расстояние; весовая характеристика кода; веро­ятность необнаруженной ошибки; оптимальность кода; коэффициент ложных переходов.

Длина кодаn—число разрядов (символов), состав­ляющих кодовую комбинацию.

Основание кодаm—количество отличающихся друг от друга значений импульсных признаков, используемых в кодовых комбинациях. Для случая двоичных кодовm=2. В качестве значений импульсных признаков ис­пользуются цифры 0 и 1.

Мощность кодаNр —число кодовых комбинаций (рабо­чих кодовых слов), используемых для передачи сообщений.

Полное число кодовых комбинацийN— число всех воз­можных комбинаций, равноеm n (для двоичных кодовN=2 n ).

Число проверочных символов r—количество символов (разрядов) кодовой комбинации, необходимых для коррекции ошибок. Это число характеризует абсолютную избыточность кода.

В теории кодирования под избыточностью кодаR по­нимают относительную избыточность, равную отношению числа проверочных символов к длине кода:R=r/n.

В более общем случае эта формула может быть приве­дена к виду

Скорость передачи кодовых комбинаций—отношение числа информационных символов к длине кода:R’=k/n.

Вес кодовой комбинации(кода)—количество еди­ниц в кодовой комбинации. Например, кодовая комби­нация 101100110 характеризуется длиной кодаn=9 и весом=5.

Кодовое расстояниеdмежду двумя кодовы­ми комбинациями—число одноименных разрядов с раз­личными символами. Практически кодовое расстояние выражается как вес суммы по модулю два кодовых ком­бинаций. Например, для определения кодового расстоя­ния между комбинациями 10010111 и 00100110 необхо­димо просуммировать их по модулю два. Полученная в результате суммирования новая кодовая комбинация характеризуется весом=4. Следовательно, кодовое расстояние между исходными комбинациями d=4.

Весовая характеристика кодаW() — число кодовых комбинаций веса.Например, для кода, содержащего кодовые комбинации 00000, 01110, 10101 и 11011, весо­вая характеристикаW(0)=l,W(3)=2,W(4)=1, т. е. данный код состоит из одного кодового слова веса 0, двух слов веса 3 и одного слова веса 4.

Вероятность необнаруженной ошибкиРн.о—это веро­ятность такого события, при котором принятая кодовая комбинация отличается от переданной, а свойства дан­ного кода не позволяют определить факт наличия ошибки.

Оптимальность кода—свойство такого кода, который обеспечивает наименьшую вероятность необнаружения ошибки среди всех кодов той же длиныnи избыточностиr.

Источник

Общие характеристики кодов

Рассмотрим общие принципы формирования сигналов в линии. Сигнал, передаваемый по линии, можно представить в следующем виде:

Здесь п — порядковый номер символа; ап(k) — k-е значение символа (kÎ ту); ту — число уровней кода; Si(t) — функция, описывающая форму импульсов. Для двоичного кода а(k) принимает два значения:, для троичного сигнала , а(3) = +1/2. В общем случае при принятии нормирующих условий

остальные уровни будут иметь величину

где аср — значение символа, соответствующего среднему уровню кода.

Для симметричных кодов аср = 0, и тогда одна половина уровней принимает положительные значения, другая — отрицательные, а при нечетном числе уровней один из них (средний) принимает значение 0. При этом значения а(k) появляются с определенными вероятностями которые зависят от статистических свойств исходной двоичной последовательности и типа преобразователя двоичного кода в линейный, а среднее значение сигнала можно определить следующим образом:

Статистические свойства коэффициентов а(k) и спектр S2(f), соответствующий форме используемых импульсов, характеризуют свойства сигнала в линии. Поэтому формирование требуемого энергетического спектра может быть осуществлено соответствующим изменением структуры импульсной последовательности и выбором импульсов нужной формы.

Учитывая, что на вероятности появления символов исходного двоичного сигнала не могут быть наложены ограничивающие условия, код, используемый в линии, должен обладать некоторой избыточностью, позволяющей удовлетворить дополнительные требования.

Элементом видеоимпульсного сигнала называется любое возможное сочетание видеоимпульсов и пауз внутри тактового интервала Т, отведенного для передачи одного символа информации. Если принять, что импульсы имеют прямоугольную форму, их длительность равна Τ или Т/2, фронт совпадает с началом или серединой тактового интервала, а амплитуда равна А/2, то возможное число разнотипных элементов видеоимпульсных сигналов Sk(t) составит девять (рис. 4.19).

Рис. 4.19. Элементы видеоимпульсных сигналов

При передаче «1» и «0» исходной информации может использоваться комбинация двух любых элементов видеоимпульсного сигнала Si (t) и Sj(t). В этом случае число двоичных видеоимпульсных сигналов С92 = 36. Кроме того, в ЦТС могут применяться многоэлементные видеоимпульсные сигналы (передача одного символа информации осуществляется с помощью нескольких элементов), а также многопозиционная (многоуровневая) модуляция отдельных элементов (например, для каждого элемента предусматривается несколько градаций амплитуды). Таким образом, видеоимпульсные сигналы отличаются весьма большим многообразием.

Однако следует учесть, что далеко не все видеоимпульсные сигналы отвечают требованиям, предъявляемым к цифровым сигналам, которые предназначены для передачи по линии. Вне зависимости от конкретных условий сравнение цифровых сигналов удобно производить по потенциальной помехоустойчивости при идеальных условиях, которая зависит от эквивалентной мощности Рэ элементов этого сигнала Si(t) и Sj(t), т.е.

Кроме того, для оценки различных видов видеоимпульсных сигналов важными являются параметры, оценивающие среднее значение вероятности присутствия тактовой частоты в цифровом сигнале и устойчивость ее признаков. В табл. 4.4 даны некоторые виды видеоимпульсных сигналов. Кроме мощности Рэ указаны также значения параметра РТ, характеризующего среднее значение вероятности присутствия тактовой частоты в цифровом сигнале при равной вероятности передачи двоичных символов, и параметра КТ, характеризующего устойчивость признаков тактовой частоты при различных предельно возможных вероятностях передачи двоичных символов, т.е.

Некоторые виды видеоимпульсных сигналов

Элементы сигналов (см. рис. 4.19), используемые для передачи

При передаче по линии сигналов, у которых Кt= 0, необходимо предусматривать некоторые дополнительные меры для повышения устойчивости признаков тактовой частоты с целью поддержания нормальных условий работы цепей тактовой синхронизации.

Из приведенных в таблице данных видно, что одним из наиболее эффективных является биимпульсный сигнал, который благодаря сбалансированности каждого элемента S3(t) и S4(t) обладает предельной помехоустойчивостью и максимальным значением параметра устойчивости признаков тактовой частоты. Однако этот сигнал имеет относительно высокую минимальную верхнюю частоту спектра (см. рис. 4.17), которая определяется как первая гармоника периодической последовательности элементов сигнала. Этот недостаток может быть скомпенсирован реализацией многоуровневой модуляции элементов биимпульсного сигнала, при которой, как будет показано ниже, снижается значение тактовой частоты.

С целью повышения стабильности признаков тактовой частоты для большинства видеоимпульсных сигналов требуется дополнительное преобразование цифровой информации путем изменения ее статистических свойств. Если изменение статистических свойств исходной двоичной информации происходит при некоторых определенных условиях (например, заданном количестве подряд следующих 0), то в результате формируются так называемые неалфавитные коды. Если же статистические свойства исходной двоичной последовательности изменяются путем ее деления на группы с постоянным числом тактовых интервалов и последующего преобразования этих групп по определенному алфавиту в группы символов кода с другим основанием счисления (больше двух) и, как правило, новым числом тактовых интервалов, то в результате формируются алфавитные коды.

Среди неалфавитных кодов наибольшее распространение получили коды типов HDBn и BnZS, в которых последовательность двоичных «0» длиной (п + 1) символов заменяется определенным сочетанием импульсов и пауз. В указанных кодах используются все три элемента сигнала ЧПИ, однако имеются нарушения условия чередования полярности импульсов. Предельная помехоустойчивость таких кодов совпадает с величиной, полученной для ЧПИ, а минимальная верхняя частота спектра увеличивается за счет сокращения числа элементов S9(t), не содержащих признаков тактовой частоты, до значения (0,6. 0,7)ft.

Алфавитное кодирование характеризуется избыточностью преобразования двоичной информации (2п Будет полезно почитать по теме:

Источник