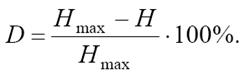избыточность равномерного двоичного кода
Энтропия и избыточность алфавита
Энтропия алфавита – это количество информации, приходящееся на один символ. Символы равновероятного алфавита несут максимальную информационную нагрузку
Алфавиты природных языков не являются равновероятными. Например, относительная частота появления отдельных символов русского языка изменяется от 0,175 до 0,002.
Вследствие статистических свойств алфавита информационная нагрузка на один символ снижена на
Избыточностью алфавита называется уменьшение информационной нагрузки на один символ вследствие неравновероятности и взаимозависимости появления его символов.
Информационная избыточность, характеризующая относительную недогруженность алфавита рассчитывается так:
Равномерные коды
Равномерные кодыхарактеризуются минимальной разрядностью кодовых слов, которая рассчитывается по формуле
где N – объем исходного алфавита А;
M – объем кодового алфавита В;
[logM N] означает целую часть числа logM N
Рассмотрим эти формулы для случая двоичного кодирования (т. е. при М = 2). Минимальная разрядность равномерного кода для алфавита объемом 8 символов будет равна
А для 9-буквенного алфавита
Неравномерные коды
Неравномерные кодыхарактеризуются средней длиной кодового слова
li – длина кодового слова i-го символа;
pi – вероятность появления i-го символа;
N – объем исходного алфавита.
Например, если алфавит А = <a, b, c, d, e> с вероятностями появления символов в сообщении (pa = 0,5; pb = 0,2; pc = 0,1; pd = 0,15; pe = 0,05) закодирован двоичным неравномерным кодом (a – 0; b – 10; c – 1110; d – 110; e – 1111), то средняя длина кодового слова для такого алфавита будет
Таким образом, средняя длина кодового слова есть сумма длин всех кодовых слов, взятых с весом, равным вероятности появления кодируемого символа.
Количество и объем информации
Оптимальное кодирование
Метод Шеннона – Фано
Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в строку).
Шаг 2. Не меняя порядка символов, делим их на две группы так, чтобы суммарные вероятности символов в группах были по возможности равны.
Шаг 3. Приписываем группе слева «0», а группе справа «1» в качестве элементов их кодов.
Шаг 4. Просматриваем группы. Если число элементов в группе более одного, идем на Шаг 2. Если в группе один элемент, построение кода для него завершено.
Метод Хаффмана
Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в столбец).
Шаг 2. Объединяем два символа с наименьшими вероятностями. Символу с большей вероятностью приписываем «1», символу с меньшей – «0» в качестве элементов их кодов.
Шаг 3. Считаем объединение символов за один символ с вероятностью, равной сумме вероятностей объединенных символов.
Шаг 4. Возвращаемся на Шаг 2 до тех пор, пока все символы не будут объединены в один с вероятностью, равной единице.
MT1402: Теоретические основы информатики. Имитационное моделирование
На первый взгляд это противоречит первой теореме Шеннона, утверждающей, что всегда можно предложить способ кодирования, при котором избыточность будет сколь угодно малой величиной. На самом деле это противоречие возникло из-за того, что до сих пор мы ограничивали себя алфавитным кодированием.
При алфавитном кодировании передаваемое сообщение представляет собой последовательность кодов отдельных знаков первичного алфавита. Однако возможны варианты кодирования, при которых кодовый знак относится сразу к нескольким буквам первичного алфавита (будем называть такую комбинацию блоком) или даже к целому слову первичного языка. Кодирование блоков понижает избыточность. В этом легко убедиться на простом примере.
очевидно, будет означать «ИНФОРМАТИКА ИНТЕРЕСНАЯ НАУКА».
Легко оценить, что при средней длине русского слова %%K(r) = 6,3%% буквы (5,3 буквы + пробел между словами) средняя информация на знак первичного алфавита оказывается равной %%I(A) = \frac
Еще более эффективным окажется кодирование в том случае, если сначала установить относительную частоту появления различных слов в текстах и затем использовать код Хаффмана. Подобные исследования провел в свое время Шеннон: по относительным частотам 8727 наиболее употребительных в английском языке слов он установил, что средняя информация на знак первичного алфавита оказывается равной 2,15 бит.
Пример. Пусть первичный алфавит состоит из двух знаков а и b с вероятностями, соответственно, 0,75 и 0,25. Сравнить избыточность кода Хаффмана при алфавитном и блочном двухбуквенном кодировании.
При алфавитном кодировании:
| знак | %%p_i%% | Код |
|---|---|---|
| a | 0.75 | 0 |
| b | 0.25 | 1 |
$$I(А) = 0,811, K(A,2) = 1, Q(A,2) = 0,233$$
При блочном двухбуквенном кодировании (очевидно, %%p_
| знак | %%p_i%% | Код |
|---|---|---|
| aa | 0.562 | 0 |
| ab | 0.188 | 11 |
| ba | 0.188 | 100 |
| bb | 0.062 | 101 |
Таким образом, блочное кодирование обеспечивает построение более оптимального кода, чем алфавитное. При использовании блоков большей длины (трехбуквенных и более) избыточность стремится к 0 в полном соответствии с первой теоремой Шеннона.
Избыточность равномерного двоичного кода
На этом шаге мы рассмотрим равномерное алфавитное двоичное кодирование; байтовый код.
Iвер 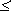
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:
1 Кбайт = 2 10 байт = 1024 байт (килобайт)
1 Мбайт = 2 20 байт = 1024 Кбайт (мегабайт)
1 Гбайт = 2 30 байт = 1024 Мбайт (гигабайт)
1 Тбайт = 2 40 байт = 1024 Гбайт (терабайт)
Использование 8-битных цепочек позволяет закодировать 2 8 =256 символов, что превышает оцененное выше N и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Вторая часть кодовой таблицы – онасчитается расширением основной – охватывает коды в интервале от 128 до 255 (первый бит всех кодов 1). Она используется для представления символов национальных алфавитов (например, русского или греческого), а также символов псевдографики. Для этой части также имеются стандарты, например, для символов русского языка это КОИ–8, КОИ–7 и др.
Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их лексикографическому порядку (т.е. порядку следования в алфавите) – это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.
Равномерные и неравномерные коды.
Дата добавления: 2015-08-14 ; просмотров: 32540 ; Нарушение авторских прав
Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Соответственно, кодирование называется равномерным, если соответствующий ему код имеет постоянную длину. В настоящее время в информатике более употребительно равномерное кодирование, оно проще и более удобно. В компьютерах при кодировании информации в основном используются равномерные коды, соответствующие размерам компьютерных ячеек.
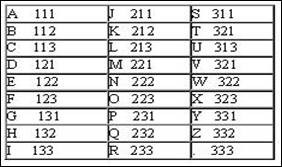
Другим интересным примером равномерного кода является код Трисиме, в котором знакам латинского алфавита ставятся в соответствие кодовые слова длины 3 над алфавитом из 3-х символов: <1, 2, 3>. Этот код представлен в следующей таблице :
Понятно, что код Трисиме не может кодировать более чем 3 3 =27 символов.
Число букв в алфавите кода называется основанием кода, а длина кодовых слов равномерного кода называется порядком кода. Коды с основанием 2, как уже говорилось, называются двоичными, а с основанием 3 – троичными, и так далее. Так код Бодо имеет основание 2, а порядок 5, а у кода Трисиме и основание, и порядок равны 3.
Код называется неравномерным (или кодом переменной длины), если его кодовые слова имеют разное число букв (неодинаковую длину слов). Соответственно, кодирование называется неравномерным, если соответствующий ему код неравномерный.
Типичным примером неравномерного кода является телеграфный код, который принято называть азбукой Морзе. На следующей таблице представлен код азбуки Морзе для русского алфавита:
| A | • − | И | • • | P | • − • | Ш | − − − − | • − − − − | − − − − • | |
| Б | − • • • | Й | • − − − | С | • • • | Щ | − − • − | • • − − − | − − − − − | |
| В | • − − | К | − • − | Т | − | Ъ | • − − • − • | • • • − − | Точка | • • • • • • |
| Г | − − • | Л | • − • • | У | • • − | Ь | − • • − | • • • • − | Запятая | • − • − • − |
| Д | − • • | М | − − | Ф | • • − • | Ы | − • − − | • • • • • | / | − • • − • |
| Е | • | H | − • | Х | • • • • | Э | • • − • • | − • • • • | ? | • • − − • • |
| Ж | • • • − | О | − − − | Ц | − • − • | Ю | • • − − | − − • • • | ! | − − • • − − |
| З | − − • • | П | • − − • | Ч | − − − • | Я | • − • − | − − − • • | @ | • − − • − • |
Американский изобретатель телеграфа Сэмюель Морзе разработал этот код в 1838 году для передачи телеграфных сообщений в виде последовательности электрических сигналов, передаваемых от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Этот код был придуман Морзе задолго до научных исследований
 |
| СэмюэлМорзе (1791-1872) |
относительной частоты появления различных букв в текстах, но, тем не менее, Морзе при составлении кода использовал принцип частоты букв. Буквам, используемым чаще, им присвоены короткие кодовые комбинации, редко используемым буквам – длинные. Морзе оценил относительную частоту букв английского языка подсчетом литер в ячейках типографской наборной машины. Наиболее часто используемой букве «Е» (в английском языке) он присвоил наиболее короткий код «точка». Следующей по количеству литер букве он присвоил код несколько большей длительности и так далее.
При составлении азбуки Морзе для букв русского алфавита учет относительной частоты букв не производился, и это повысило его избыточность. Расчеты избыточности кода Морзе на основании проведенных исследований частоты появления букв показали, что для букв английского алфавита она составляет 19%, для букв русского алфавита 22%.
Преимущество у неравномерных кодов перед равномерными как раз и состоит в том, что сообщения можно передавать более экономным способом, так как часто передаваемые кодовые слова более короткие, а значит, кодовая последовательность может иметь меньшую длину, чем для равномерных кодов. Ниже это будет показано.
Но у неравномерных кодов есть серьезный недостаток по сравнению с равномерными кодами. У равномерных кодов кодовая последовательность всегда декодируется однозначно за счет того, что кодовые слова имеют одинаковую длину (кодовая последовательность легко делится на кодовые слова). Но не для всех неравномерных кодов достигается однозначность декодирования кодовых последовательностей. Мы уже видели это, пытаясь рассматривать азбуку Морзе как двоичный код.
Этот код неравномерный (кодовые слова разной длины).
Закодируем последовательность сообщений: s7s7. Имеем F(s7s7)=B=111111. Но эта последовательность может быть декодирована и по-другому, так как: B=F(s3s3s3)= F(s1s3s7)=F(s3s7s1)=F(s1s1s1s1s1s1s1s). Как видим, способов декодирования много (подсчитайте: сколько их?). Неоднозначно декодируется и следующая последовательность:
11011011 (а сколько здесь способов декодирования?). Очевидно, что такой код практически использовать нельзя. А если мы изменим код так, чтобы он стал равномерным, например, доопределим функцию F так:
то теперь никаких проблем с декодированием не будет.
2.2. Равномерное алфавитное двоичное кодирование. Байтовый код
В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное I ( А) = log2 N. Формировать признак конца знака не требуется, поэтому для определения длины кода можно воспользоваться формулой К(А,2) > log2 N. Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при этом недопустимы сбои, например, пропуск (непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи или иными способами. С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.
Другим важным примером использования равномерного алфавитного кодирования является представление символьной (знаковой) информации в компьютере. Чтобы определить длину кода, необходимо начать с установления количества знаков в первичном алфавите. Компьютерный алфавит должен включать:
Байт наряду с битом может использоваться как единица измерения количества информации в сообщении. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным. Пусть имеется некоторое сообщение (последовательность знаков); оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона дает Iвер, а объемная мера пусть равна Iоб; соотношение между этими величинами вытекает из (2.12):
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:
1 Кбайт = 2 10 байт = 1024 байт (килобайт)
1 Мбайт = 2 20 байт = 1024 Кбайт (мегабайт)
1 Гбайт = 2 30 байт = 1024 Мбайт (гигабайт)
1 Тбайт = 2 40 байт = 1024 Гбайт (терабайт)
Использование 8-битных цепочек позволяет закодировать 2 8 =256 символов, что превышает оцененное выше N и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Однако недостаточно только условиться об определенной длине кода. Ясно, что способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьмибитных цепочек, очень много. По этой причине для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов. Подобное согласование осуществляется в форме стандартизации кодовых таблиц.
Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0). В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31), вырабатываемые при использовании клавиатуры. Ниже приведены некоторые ФSC-коды: