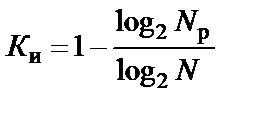если кодовые комбинации содержат постоянное число символов такой код называется
Кодирование информации
| Определение: |
| Кодирование информации (англ. information coding) — отображение данных на кодовые слова. |
Обычно в процессе кодирования информация преобразуется из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения или автоматической обработки. В более узком смысле кодированием информации называют представление информации в виде кода. Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Содержание
Код [ править ]
Виды кодов [ править ]
Все вышеперечисленные коды являются однозначно декодируемыми — для такого кода любое слово, составленное из кодовых слов, можно декодировать только единственным способом.
Примеры кодов [ править ]
Однозначно декодируемый код [ править ]
| Определение: |
| Однозначно декодируемый код (англ. uniquely decodable code) — код, в котором любое слово составленное из кодовых слов можно декодировать только единственным способом. |
Пусть есть код заданный следующей кодовой таблицей:
[math]a_1 \rightarrow b_1[/math]
[math]a_2 \rightarrow b_2[/math]
[math]a_k \rightarrow b_k[/math]
Код является однозначно декодируемым, только тогда, когда для любых строк, составленных из кодовых слов, вида:
Всегда выполняются равенства:
Заметим, что если среди кодовых слов будут одинаковые, то однозначно декодировать этот код мы уже не сможем.
Префиксный код [ править ]
| Определение: |
| Префиксный код (англ. prefix code) — код, в котором никакое кодовое слово не является префиксом какого-то другого кодового слова. |
Предпочтение префиксным кодам отдается из-за того, что они упрощают декодирование. Поскольку никакое кодовое слово не выступает в роли префикса другого, кодовое слово, с которого начинается файл, определяется однозначно, как и все последующие кодовые слова.
Пример кодирования [ править ]
Закодируем строку [math]abacaba[/math] :
Такой код можно однозначно разбить на слова:
[math]00\ 01\ 00\ 1\ 00\ 01\ 00[/math]
Преимущества префиксных кодов [ править ]
Недостатки префиксных кодов [ править ]
Пример неудачного декодирования [ править ]
Предположим, что последовательность [math]abacaba[/math] из примера передалась неверно и стала:
[math]c^<**>(abacaba) = 0001001\ 1\ 00100[/math]
Разобьем ее согласно словарю:
[math] 00\ 01\ 00\ 1\ 1\ 00\ 1\ 00[/math]
[math]a\quad b\quad a\ c\ c\quad a\ c\ a[/math]
Полученная строка совпадает только в битах, которые находились до ошибочного, поэтому декодирование неравномерного кода, содержащего ошибки, может дать абсолютно неверные результаты.
Не префиксный однозначно декодируемый код [ править ]
Как уже было сказано, префиксный код всегда однозначно декодируем. Обратное в общем случае неверно:
Мы можем ее однозначно декодировать, так как знаем, что слева от двойки и справа от тройки всегда стоит единица.
После декодирования получаем: [math]abbca[/math]
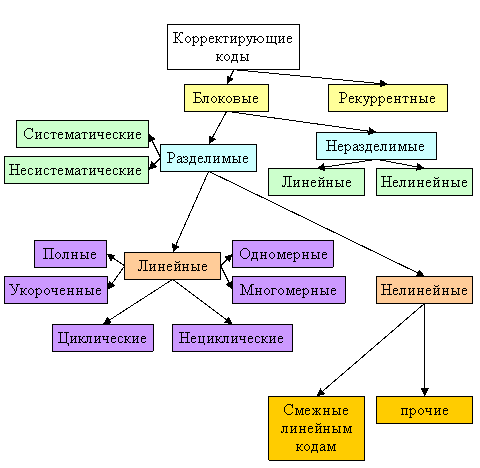
§Классификация корректирующих кодов.
Разделимым кодом разрядности n называется код, в каждой комбинации которого можно выделить позиции, на которых стоят информационные и проверочные символы.
Распространение получили только коды, у которых во всех комбинациях эти позиции постоянны.
Разделимые коды обозначаются как (n, k)- код, где n – разрядность, а k – число информационных символов.
Блоковые разделимые коды образуются при первом способе построения комбинаций корректирующего кода.
Разделимый код содержит N = 2 k комбинаций.
Неразделимым называется код, в комбинациях которого невозможно выделить позиции, на которых стоят информационные и проверочные символы. Неразделимые коды образуются при помощи второго способа построения комбинаций.
Пример: код с постоянным весом, равным 2, является неразделимым кодом.
Разделимый блоковый код называется систематическим, если в каждой его комбинации первые k позиций заняты информационными символами, а последние r позиций – проверочными.
Если комбинации кода имеют другую структуру, то код называется несистематическим.
Например, несистематическим является код Хемминга со структурой комбинаций V = (b1 b2 a1 b3 a2 a3 a4). Проверочные символы занимают позиции равные степеням двойки.
§Принцип исправления ошибок в комбинациях линейных кодов.
Чтобы распечатать файл, скачайте его (в формате Word).
Если кодовые комбинации содержат постоянное число символов такой код называется
Классификация рассматриваемых в данной главе методов кодирования приведена на рис. 5.2. Эта классификация не является исчерпывающей, в нее включены лишь некоторые методы, которые широко используются в современных системах связи.
Коды можно разделить на две самостоятельные группы. К первой относятся коды, использующие все возможные комбинации – неизбыточные коды. В литературе их еще называют простыми, или первичными. Ко второй группе относятся коды, использующие лишь определенную часть всех возможных комбинаций, такие коды называются избыточными. Оставшаяся часть комбинаций используется для обнаружения или исправления ошибок, возникающих при передаче сообщений. В этих кодах количество разрядов кодовых комбинаций можно условно разделить на определенное число разрядов, предназначенных для информации (информационные разряды), и число разрядов, предназначенных для коррекции ошибок (проверочные разряды).
Обе группы кодов, в свою очередь, подразделяются на равномерные и неравномерные. Равномерные коды – это коды, все кодовые комбинации которых содержат постоянное количество разрядов. Неравномерные коды содержат кодовые комбинации с различным числом разрядов. Ввиду того что неравномерные избыточные коды не нашли применения на практике из-за сложности их технической реализации, в дальнейшем их рассматривать не будем.
Все корректирующие (избыточные) коды делятся на два больших класса: блочные и непрерывные коды (рис. 5.2).
При кодировании блочным кодом последовательность 




В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. Неразделимые коды не имеют четкого разделения кодовой комбинации на информационные и проверочные символы. К ним относятся коды с постоянным весом и коды Плоткина [2].
Разделимые блочные коды, в свою очередь, делятся на несистематические и систематические. Наиболее многочисленный класс разделимых кодов составляют систематические коды. Основная их особенность в том, что проверочные символы образуются как линейные комбинации информационных символов. К систематическим кодам относятся коды с проверкой на четность, коды с повторением, корреляционный, инверсный, коды Хэмминга, Голея, Рида-Маллера, Макдональда, Варшамова, с малой плотностью проверок на четность, итеративный код [2].
В несистематических кодах проверочные символы представляют собой суммы подблоков с 
Разновидностью систематических кодов являются циклические коды. Кроме всех свойств систематического кода, циклические коды имеют следующее свойство: если некоторая кодовая комбинация принадлежит коду, то получающаяся путем циклической перестановки символов новая комбинация также принадлежит данному коду. К наиболее известным циклическим кодам относятся простейшие коды, коды Хэмминга, Боуза-Чоудхури-Хоквингема, мажоритарные, коды Файра, Абрамсона, Миласа-Абрамсона, Рида-Соломона, компаундные коды.
Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
Классификация кодов
Применяемые в технике связи коды можно классифицировать по ряду специфических признаков.
По длине кодов и взаимному расположению в них символов различают равномерные и неравномерные коды.
Равномерные коды имеют одинаковую длину комбинаций. Для равномерного кода число возможных комбинаций составляет 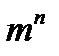

Неравномерные коды отличаются тем, что кодовые комбинации у них отличаются друг от друга не только взаимным расположением символов, но и их количеством при минимизации средней длины кодовой последовательности. Это приводит к тому, что различные комбинации имеют различную длительность.
По признаку помехозащищенности коды, как и методы кодирования, делят на примитивные (первичные, простые, безызбыточные) и помехоустойчивые (корректирующие, избыточные).
Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются примитивными или кодами без избыточности. В простых равномерных кодах превращение одного символа комбинации в другой, например 0 в 1 или 1 в 0, приводит к появлению новой разрешенной комбинации, т.е. к ошибке в принятом сообщении.
Примитивное, или безызбыточное, кодирование применяется для согласования алфавита источника и алфавита канала. Отличительное свойство примитивного кодирования состоят в том, что избыточность дискретного источника, образованного выходом примитивного кодера, равна избыточности источника на входе кодера. Примитивное кодирование используется также в целях шифрования передаваемой информации для ее защиты от несанкционированного доступа и повышения устойчивости работы устройств синхронизации систем связи.
В помехоустойчивых кодах для передачи сообщения используются не все кодовые комбинации, а только некоторая их часть (разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов обеспечиваются введением в кодовые комбинации дополнительных (избыточных) символов.
В настоящее время разработано большое число помехоустойчивых кодов, которые могут быть классифицированы по различным признакам.
По способу кодирования помехоустойчивые коды обычно разбивают на два класса: блочные и непрерывные.
Блочное кодирование состоит в том, что последовательность символов источника сообщений (последовательность нулей и единиц) разделяется на блоки, которые обычно называют кодовыми комбинациями. На практике количество символов в блоке может быть в пределах от 3 до нескольких сотен.
Блоки, содержащие k символов каждый, по определенному закону преобразуются кодером в n-символьные блоки, причем n > k. Например, схема блочного кодера
Каждый символ выходного блока информации получается как сумма по модулю 2 нескольких символов входного блока, для чего используются n сумматоров по модулю 2. Совокупность всех возможных кодовых комбинаций при блочном способе кодирования, и есть блочный код.
Непрерывные коды характеризуются тем, что кодирование и декодирование информационной последовательности символов осуществляется без ее разбиения на блоки. Каждый символ выходной последовательности получается как результат некоторых операций над символами входной последовательности. Кодирование и декодирование непрерывных кодов носит непрерывный характер. При этом результат декодирования предыдущих или последующих символов может повлиять на декодирование текущего символа. Среди непрерывных кодов наиболее часто применяют сверточные коды.
Блочные коды подразделяются на разделимые и неразделимые. К разделимым относятся коды, кодовые комбинации которых состоят из двух частей: информационной и проверочной. Обычно проверочные символы получаются посредством некоторых операций над информационными символами. Разделимые коды условно обозначают в виде (n, k), где n – число символов в кодовой комбинации, k – число информационных символов. Число проверочных символов в разделимых блочных кодах равно r = n-k.
К неразделимым относятся коды, кодовые комбинации которых нельзя разделить на информационные и проверочные части.
Самый большой класс разделимых кодов составляют систематические коды, у которых значения проверочных символов определяются в результате проведения линейных операций над информационными символами. Последовательность линейных операций и число проверочных символов определяется тем, сколько ошибок должен исправлять и обнаруживать данный код. Проверочные символы могут располагаться на любом месте кодовой комбинации. Однако обычно проверочные символы записывают к информационным символам справа, т.е. располагают на месте младших разрядов.
Например, рассмотрим схему наиболее простого систематического кодера (5,4). Здесь всего лишь один проверочный символ формируется из информационных символов путем их суммирования по модулю 2. Этот код называют кодом с проверкой на четность. Так как новую разрешенную комбинацию систематического кода можно получить линейными преобразованиями двух разрешенных, то такие коды часто называют линейными или групповыми.
К несистематическим (нелинейным) относятся коды, в которых проверочные символы формируются за счет некоторых нелинейных операций над информационными символами. Примером нелинейного кода является код Бергера.
4.4 Основные характеристики помехоустойчивых кодов
Основными характеристиками помехоустойчивых кодов являются:
1. Длина кода n – это число символов в кодовой комбинации. Например, комбинация 11010 состоит из пяти символов, следовательно, n=5. Если все кодовые комбинации содержат одинаковое число символов, то код называется равномерным. В неравномерных кодах длина кодовых комбинаций может быть разной.
2. Основание кода m – это число различных символов в коде. Для двоичных кодов символами являются 1 и 0, поэтому m=2.
5. Избыточность кода Ки в общем случае определяется выражением
и показывает, какая доля длины кодовой комбинации не используется для передачи информации, а используется для повышения помехоустойчивости кода. Для разделимых кодов

где величина k/n называется относительной скоростью кода.
6. Кодовое расстояние d(А,В) – это число позиций, в которых две кодовые комбинации А и В отличаются друг от друга. Например, если А=01101, В=10111, то d(А,В)=3. Кодовое расстояние между комбинациями А и В может быть найдено в результате сложения по модулю 2 одноименных разрядов комбинаций, а именно
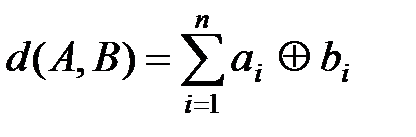
где ai и bi – i-е разряды кодовых комбинаций A и B; символ Å обозначает сложение по модулю 2.
Кодовое расстояние между различными комбинациями конкретного кода может быть различным. Так, для первичных кодов это расстояние для различных пар кодовых комбинаций может принимать значения от единицы до величины длины кода.
7. Минимальное кодовое расстояние dmin – это минимальное расстояние между разрешенными кодовыми комбинациями данного кода. Минимальное кодовое расстояние является основной характеристикой корректирующей способности кода. В первичных (безызбыточных) кодах все комбинации являются разрешенными, поэтому минимальное кодовое расстояние для них равно единице (dmin=1). Такие коды не способны обнаруживать и исправлять ошибки. Для того чтобы код обладал корректирующими способностями, его минимальное кодовое расстояние должно быть не менее двух (dmin ³ 2).
Для обнаружения всех ошибок кратностью s и менее, минимальное кодовое расстояние должно удовлетворять условию
Если код используется для исправления ошибок кратности не более t, то минимальное кодовое расстояние должно иметь значение
Для обнаружения s ошибок и исправления t ошибок должно выполняться условие
Таким образом, задача построения кода с заданной корректирующей способностью сводится к обеспечению необходимого кодового расстояния. Увеличение dmin приводит к росту избыточности кода. При этом желательно, чтобы число проверочных символов r было минимальным. В настоящее время известен ряд верхних и нижних границ, которые устанавливают связь между кодовым расстоянием и числом проверочных символов.
Необходимые сведения из теории кодирования
Длина кодовой комбинации – количество символов в комбинации, обозначаемое буквой n.
Представление информации кодом
Для примера рассмотрим простую систему с основанием m = 2 в виде обычного реле. Как известно, в реле может быть только два сигнала – либо контакт замкнут, либо разомкнут, соответственно передать можно только два сигнала – либо 1 когда контакт реле замкнут и на объекте присутствует напряжение, или 0, если контакт разомкнут, и напряжение на объекте нет. Ниже представлена система из шести реле и возможные кодовые комбинации при различных положениях реле:
Представленную выше систему часто используют для сигнализации. Например, нормальной работа системы будет считаться тогда, когда замкнуты все реле (комбинация 111111). Если на каком-то участке произошел сбой и контакт не был замкнут, то по сигналу легко определить на каком участке произошел сбой. Например, при комбинации 110111 понятно что проблема на участке с Р4, что значительно упрощает устранение причины отказа. Также такую информацию вполне возможно представлять в бумажном виде (распечатанном, например), на перфолентах, в цифровом виде.
Длина всех рассмотренных комбинаций в этом примере равна шести, то есть n = 6 (110111,101101 и так далее).
Также в кодовых комбинациях присутствует такое понятие как вес комбинации, который равен количеству единичных символов в коде и обозначается буквой l. Для комбинации 101101 вес l = 4, 111111 вес l = 6, 110111 вес l = 5.
Классификация кодов
Для удобства использования коды классифицируют. Рассмотрим основные классификации:
Очень часто в технике применяют код типа 2 из 5, имеющего число комбинаций:
У всех комбинаций присущ одинаковый вес l = 2.
Вес определенной n членной комбинации изменяющейся от 0 до n, в общем случае можно выразить биномом Ньютона:
Общее число комбинаций для n = 5:
Рассмотренный выше код (1.2) неполный, так как при его формировании было использовано только восемь комбинаций четного веса при возможных шестнадцати. Из оставшихся восьми нечетных комбинаций также можно сформировать неполный нечетный код.
Код 2 из 5 (1.1) – двухпеременный. Расстояние между смежными комбинациями в данном коде везде равно двум. Если те же комбинации расположить в другом порядке, то можно получить четырехпеременный код:
Если у кода отсутствуют арифметические свойства – он комбинаторный. Формирование комбинаторных кодов производят по законам теории соединений (перестановок, сочетаний, размещений), которая изучается в разделе математики называемом комбинаторикой. Из рассмотренных ранее кодов к комбинаторным относят нечетные, четные, равновесные.