быстрая сортировка python код
Алгоритм сортировки Quicksort на Python.
Quicksort – один из моих популярных алгоритмов сортировки. По данным Википедии он является наиболее используемым в мире (хотя я думаю, что уже несколько лет его вытесняет новый алгоритм Timsort). Quicksort был изобретен в 1961 году Тони Хоаром. Давайте перейдем непосредственно к сути этого алгоритма.
Как работает Quicksort
Quicksort – это алгоритм работающий по принципу “разделяй и властвуй”. После выбора элемента внутри массива с именем pivot (опорный элемент), этот массив разбивается на две части: первая содержит элементы этого pivot.
Как и другие алгоритмы, Quicksort состоит из двух основных функций:
Если сейчас не очень понятно, не переживайте. Дальше мы подробно разберем как все работает. С примерами, картинками и графиками.
Реализация на языке Python
В этой статье я решил не говорить подробно о самой функции Quicksort из-за ее простоты. А вот на Partition мы потратим чуть больше времени.
Функция Quicksort
Как видите, функция очень проста. Принимает на вход массив array, индекс первого элемента первым а индекс последнего элемента последним. После очень простой проверки (строка 2) разбиение выполняется вызовом функции partition(array,first,last). Эта функция возвращает числовое значение (сохраненное в q), которое определяет индекс pivot (который соответствует элементу, уже правильно расположенному в нашем массиве). После чего функция вызывается рекурсивно на двух еще не упорядоченных подпоследовательностях.
Функция Partition
Самой интересной функцией, безусловно, является функция Partition. Первое, что нужно определить, это какой элемент выбрать в качестве опорного, некоторые используют первый элемент последовательности, другие – последний: ничего не меняется.
В этой статье и последующих реализациях, буду использовать второй вариант.
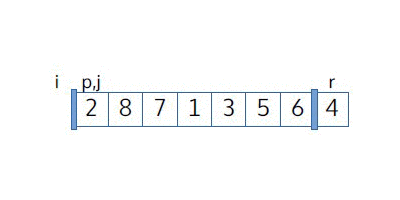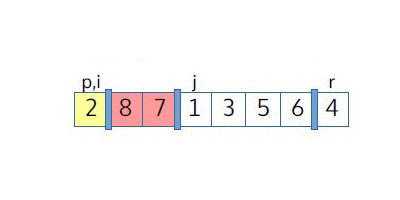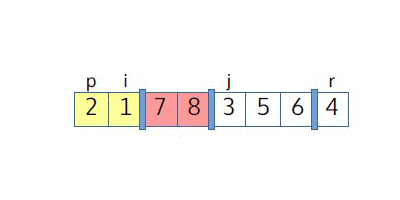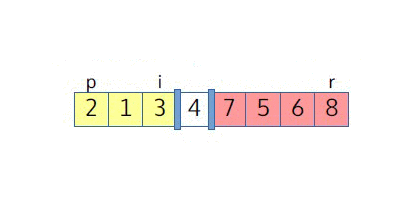
Итак, у нас есть начальный массив A, первый элемент будет A[r], а последний элемент (соответствующий pivot) будет A[p].
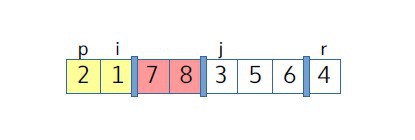
Понятно, что анализируемыми элементами являются все элементы, идущие от A[r] к A[p-1]. Эти элементы сравниваются с опорным элементом, чтобы решить, к какому разделу они относятся. При запуске Partition мы можем разделить массив на четыре части:
Что такое i и j? Это индексы, которые мы будем использовать для разделения рассматриваемых участков во время выполнения функции.
В качестве примера рассмотрим выполнение Partition. Мы видим, что j соответствует индексу первого еще не разобранного элемента. Две области, желтая и красная, соответствуют элементам, которые уже были разделены (желтая область содержит ≤-элементы, а красная область содержит >-элементы).
j-й элемент сравнивается с опорным элементом:
Пояснение в виде gif анимации.
Теперь мы можем перейти к коду:
Заключение
Сегодня мы рассмотрели алгоритм, который мне очень нравится. Надеюсь вам было полезно.
Похожие записи
Некоторое время назад у меня возникла ошибка при вызове https-адреса в pyhon. После долгих поисков…
Сравнивать даты в Python очень просто. Для этого достаточно использовать операторы сравнения. В этой статье…
JSON позволяет быстро и просто работать с несколькими данными: в различных приложениях и языках программирования.…
Быстрая сортировка в Python
Введение
Быстрая сортировка — популярный алгоритм сортировки, который часто используется вместе с сортировкой слиянием. Это алгоритм является хорошим примером эффективного алгоритма сортировки со средней сложностью O(n logn). Часть его популярности еще связана с простотой реализации.
Спонсор поста Онлайн-курс по алгоритмам на Python
Курс по алгоритмам и структурам данных на Python для новичков. Видео-уроки, домашние задания, поддержка. На курсе вы изучите следующие темы:
– Структуры данных, сортировка и поиск.
– Рекурсия, деревья, сжатие информации.
– Криптография и и блокчейн.
С 2019 года курс «читается» студентам Московского университета экономики и права им. Витте на специальностях «Прикладная информатика» и «Бизнес-информатика».
Быстрая сортировка является представителем трех типов алгоритмов: divide and conquer (разделяй и властвуй), in-place (на месте) и unstable (нестабильный).
Быстрая сортировка
Базовая версия алгоритма делает следующее:
Разделяет коллекцию на две (примерно) равные части, принимая псевдослучайный элемент и использовать его в качестве опоры (как бы центра деления). Элементы, меньшие, чем опора, перемещаются влево от опоры, а элементы, размер которых больше, чем опора, справа от него. Этот процесс повторяется для коллекции слева от опоры, а также для массива элементов справа от опоры, пока весь массив не будет отсортирован.
Когда мы описываем элементы как «больше» или «меньше», чем другой элемент — это не обязательно означает большие или меньшие целые числа, мы можем отсортировать по любому выбранному нами свойству.
К примеру, если у нас есть пользовательский класс Person, и у каждого человека есть имя и возраст, мы можем сортировать по имени (лексикографически) или по возрасту (по возрастанию или по убыванию).
Как работает Быстрая сортировка
Быстрая сортировка чаще всего не сможет разделить массив на равные части. Это потому, что весь процесс зависит от того, как мы выбираем опорный элемент. Нам нужно выбрать опору так, чтобы она была примерно больше половины элементов и, следовательно, примерно меньше, чем другая половина элементов. Каким бы интуитивным ни казался этот процесс, это очень сложно сделать.
Подумайте об этом на мгновение — как бы вы выбрали адекватную опору для вашего массива? В истории быстрой сортировки было представлено много идей о том, как выбрать центральную точку — случайный выбор элемента, который не работает из-за того, что «дорогой» выбор случайного элемента не гарантирует хорошего выбора центральной точки; выбор элемента из середины; выбор медианы первого, среднего и последнего элемента; и еще более сложные рекурсивные формулы.
Самый простой подход — просто выбрать первый (или последний) элемент. По иронии судьбы, это приводит к быстрой сортировке на уже отсортированных (или почти отсортированных) массивах.
Именно так большинство людей выбирают реализацию быстрой сортировки, и, так как это просто и этот способ выбора опоры является очень эффективной операцией, и это именно то, что мы будем делать.
Теперь, когда мы выбрали опорный элемент — что нам с ним делать? Опять же, есть несколько способов сделать само разбиение. У нас будет «указатель» на нашу опору, указатель на «меньшие» элементы и указатель на «более крупные» элементы.
Цель состоит в том, чтобы переместить элементы так, чтобы все элементы, меньшие, чем опора, находились слева от него, а все более крупные элементы были справа от него. Меньшие и большие элементы не обязательно будут отсортированы, мы просто хотим, чтобы они находились на правильной стороне оси. Затем мы рекурсивно проходим левую и правую сторону оси.
Рассмотрим пошагово то, что мы планируем сделать, это поможет проиллюстрировать весь процесс. Пусть у нас будет следующий список.
29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21,44 (high)
Выберем первый элемент как опору 29), а указатель на меньшие элементы (называемый «low») будет следующим элементом, указатель на более крупные элементы (называемый «high») станем последний элемент в списке.
29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44
29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44
29 | 21 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,99 (high),44
Этот процесс продолжается до тех пор, пока указатели low и high наконец не встретятся в одном элементе:
29 | 21,27,12,19,28 (low/high),44,78,87,66,31,76,58,88,83,97,41,99,44
28,21,27,12,19,29,44,78,87,66,31,76,58,88,83,97,41,99,44
Как видите, мы достигли того, что все значения, меньшие 29, теперь слева от 29, а все значения больше 29 справа.
Затем алгоритм делает то же самое для коллекции 28,21,27,12,19 (левая сторона) и 44,78,87,66,31,76,58,88,83,97,41,99,44 (правая сторона). И так далее.
Реализация
Сортировка массивов
Быстрая сортировка является естественным рекурсивным алгоритмом — разделите входной массив на меньшие массивы, переместите элементы в нужную сторону оси и повторите.
При этом мы будем использовать две функции — partition() и quick_sort().
Давайте начнем с функции partition():
И, наконец, давайте реализуем функцию quick_sort():
После того, как обе функции реализованы, мы можем запустить quick_sort():
Поскольку алгоритм unstable (нестабилен), нет никакой гарантии, что два 19 будут всегда в этом порядке друг за другом. Хотя это ничего не значит для массива целых чисел.
Оптимизация быстрой сортировки
Учитывая, что быстрая сортировка сортирует «половинки» заданного массива независимо друг от друга, это оказывается очень удобным для распараллеливания. У нас может быть отдельный поток, который сортирует каждую «половину» массива, и в идеале мы могли бы вдвое сократить время, необходимое для его сортировки.
Однако быстрая сортировка может иметь очень глубокий рекурсивный стек вызовов, если нам особенно не повезло в выборе опорного элемента, а распараллеливание будет не так эффективно, как в случае сортировки слиянием.
Для сортировки небольших массивов рекомендуется использовать простой нерекурсивный алгоритм. Даже что-то простое, например сортировка вставкой, будет более эффективным для небольших массивов, чем быстрая сортировка. Поэтому в идеале мы могли бы проверить, имеет ли наш подмассив лишь небольшое количество элементов (большинство рекомендаций говорят о 10 или менее значений), и если да, то мы бы отсортировали его с помощью Insertion Sort (сортировка вставкой).
Заключение
Как мы уже упоминали ранее, эффективность быстрой сортировки сильно зависит от выбора точки опоры — он может «упростить или усложнить» сложность алгоритма во времени (и в пространстве стека). Нестабильность алгоритма также может стать препятствием для использования с пользовательскими объектами.
Тем не менее, несмотря на все это, средняя сложность времени O(n*logn) в быстрой сортировки, а также его относительно небольшое потребление памяти и простая реализация делают его очень эффективным и популярным алгоритмом.
Объяснение алгоритмов сортировки с примерами на Python
В этой статье будут рассмотрены популярные алгоритмы, принципы их работы и реализация на Python. А ещё сравним, как быстро они сортируют элементы в списке.
В качестве общего примера возьмём сортировку чисел в порядке возрастания. Но эти методы можно легко адаптировать под ваши потребности.
Пузырьковая сортировка
Этот простой алгоритм выполняет итерации по списку, сравнивая элементы попарно и меняя их местами, пока более крупные элементы не «всплывут» в начало списка, а более мелкие не останутся на «дне».
Алгоритм
Сначала сравниваются первые два элемента списка. Если первый элемент больше, они меняются местами. Если они уже в нужном порядке, оставляем их как есть. Затем переходим к следующей паре элементов, сравниваем их значения и меняем местами при необходимости. Этот процесс продолжается до последней пары элементов в списке.
При достижении конца списка процесс повторяется заново для каждого элемента. Это крайне неэффективно, если в массиве нужно сделать, например, только один обмен. Алгоритм повторяется n² раз, даже если список уже отсортирован.
9–10 октября, Москва и онлайн, Беcплатно
Для оптимизации алгоритма нужно знать, когда его остановить, то есть когда список отсортирован.
Реализация
Время сортировки
Если взять самый худший случай (изначально список отсортирован по убыванию), затраты времени будут равны O(n²), где n — количество элементов списка.
Сортировка выборкой
Этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Наименьший элемент удаляется из второго списка и добавляется в первый.
Алгоритм
На практике не нужно создавать новый список для отсортированных элементов. В качестве него используется крайняя левая часть списка. Находится наименьший элемент и меняется с первым местами.
Теперь, когда нам известно, что первый элемент списка отсортирован, находим наименьший элемент из оставшихся и меняем местами со вторым. Повторяем это до тех пор, пока не останется последний элемент в списке.
Реализация
По мере увеличения значения i нужно проверять меньше элементов.
Время сортировки
Затраты времени на сортировку выборкой в среднем составляют O(n²), где n — количество элементов списка.
Сортировка вставками
Как и сортировка выборкой, этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Алгоритм перебирает второй сегмент и вставляет текущий элемент в правильную позицию первого сегмента.
Алгоритм
Переходя к другим элементам несортированного сегмента, перемещаем более крупные элементы в отсортированном сегменте вверх по списку, пока не встретим элемент меньше x или не дойдём до конца списка. В первом случае x помещается на правильную позицию.
Реализация
Время сортировки
Время сортировки вставками в среднем равно O(n²), где n — количество элементов списка.
Пирамидальная сортировка
Также известна как сортировка кучей. Этот популярный алгоритм, как и сортировки вставками или выборкой, сегментирует список на две части: отсортированную и неотсортированную. Алгоритм преобразует второй сегмент списка в структуру данных «куча» (heap), чтобы можно было эффективно определить самый большой элемент.
Алгоритм
Сначала преобразуем список в Max Heap — бинарное дерево, где самый большой элемент является вершиной дерева. Затем помещаем этот элемент в конец списка. После перестраиваем Max Heap и снова помещаем новый наибольший элемент уже перед последним элементом в списке.
Этот процесс построения кучи повторяется, пока все вершины дерева не будут удалены.
Реализация
Создадим вспомогательную функцию heapify() для реализации этого алгоритма:
Время сортировки
В среднем время сортировки кучей составляет O(n log n), что уже значительно быстрее предыдущих алгоритмов.
Сортировка слиянием
Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.
Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.
Алгоритм
Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.
Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.
Реализация
Время сортировки
В среднем время сортировки слиянием составляет O(n log n).
Быстрая сортировка
Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие — позади.
Алгоритм
Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.
Реализация
Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).
Время выполнения
В среднем время выполнения быстрой сортировки составляет O(n log n).
Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²).
Встроенные функции сортировки на Python
Иногда полезно знать перечисленные выше алгоритмы, но в большинстве случаев разработчик, скорее всего, будет использовать функции сортировки, уже предоставленные в языке программирования.
Отсортировать содержимое списка можно с помощью стандартного метода sort() :
Или можно использовать функцию sorted() для создания нового отсортированного списка, оставив входной список нетронутым:
Оба эти метода сортируют в порядке возрастания, но можно изменить порядок, установив для флага reverse значение True :
В отличие от других алгоритмов, обе функции в Python могут сортировать также списки кортежей и классов. Функция sorted() может сортировать любую последовательность, которая включает списки, строки, кортежи, словари, наборы и пользовательские итераторы, которые вы можете создать.
Функции в Python реализуют алгоритм Tim Sort, основанный на сортировке слиянием и сортировке вставкой.
Сравнение скоростей сортировок
Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.
Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.
Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.
Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.
Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.
Лучше понять эти алгоритмы вам поможет их визуализация.
Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.
Перейти к регистрации
Алгоритмы сортировки в Python
Введение
Иногда данные, которые мы храним или извлекаем в приложении, могут находится в беспорядочном состояние. И иногда возникает необходимость упорядочивания данные прежде чем их можно будет эффективно использовать. За все эти годы учеными было создано множество алгоритмов сортировки для организации данных.
В этой статье мы рассмотрим наиболее популярные алгоритмы сортировки, разберем, как они работают, и напишем их на Python. Мы также сравним, как быстро они сортируют элементы в списке.
Для простоты реализации алгоритмов сортировать числа будем в порядке их возрастания.
Пузырьковая сортировка (Bubble Sort)
Этот самый простой алгоритм сортировки который выполняет итерации по списку, сравнивая элементы попарно и меняя их местами, пока более крупные элементы не перестанут «всплывать» до конца списка, а более мелкие элементы не будут оставаться «снизу».
Объяснение
Начнем со сравнения первых двух элементов списка. Если первый элемент больше второго, мы меняем их местами. Если они уже в нужном порядке, мы оставляем их как есть. Затем мы переходим к следующей паре элементов, сравниваем их значения и меняем местами при необходимости. Этот процесс продолжается до последней пары элементов в списке.
Достигнув конца списка, повторяем этот процесс для каждого элемента снова. Хотя это крайне неэффективно. Что если в массиве нужно сделать только одну замену? Почему мы все еще повторяем, даже если список уже отсортирован? Получается нам нужно пройти список n^2 раза.
Очевидно, что для оптимизации алгоритма нам нужно остановить его, когда он закончит сортировку.
Откуда нам знать, что мы закончили сортировку? Если бы элементы были отсортированы, то нам не пришлось бы их менять местами. Таким образом, всякий раз, когда мы меняем элементы, мы устанавливаем флаг в True, чтобы повторить процесс сортировки. Если перестановок не произошло, флаг останется False, и алгоритм остановится.
Реализация
Мы можем реализовать пузырьковую сортировку в Python следующим образом:
Алгоритм работает в цикле while, прерываясь только тогда, когда никакие элементы не меняются местами. Вначале мы установили для swapped значение True, чтобы алгоритм прошел по списку хотя бы один раз.
Сложность
Сложность пузырьковой сортировки в худшем случае (когда список отсортирован в обратном порядке) равна O(n^2).
Сортировка выбором (Selection Sort)
Этот алгоритм сегментирует список на две части: отсортированные и несортированные. Он постоянно удаляет наименьший элемент из несортированного сегмента списка и добавляет его в отсортированный сегмент.
Объяснение
На практике нам не нужно создавать новый список для отсортированных элементов, мы будет обрабатывать крайнюю левую часть списка как отсортированный сегмент. Затем мы ищем во всем списке наименьший элемент и меняем его на первый элемент.
Теперь мы знаем, что первый элемент списка отсортирован, мы получаем наименьший элемент из оставшихся элементов и заменяем его вторым элементом. Это повторяется до тех пор, пока последний элемент списка не станет оставшимся элементом для изучения.
Реализация
Мы видим, что по мере того как i увеличивается, нам нужно проверять все меньше элементов.
Сложность
Сложность сортировки выбором в среднем составляет O(n^2).
Сортировка вставками (Insertion Sort)
Как и Сортировка выбором, этот алгоритм сегментирует список на отсортированные и несортированные части. Он перебирает несортированный сегмент и вставляет просматриваемый элемент в правильную позицию отсортированного списка.
Объяснение
Предполагается, что первый элемент списка отсортирован. Затем мы переходим к следующему элементу, назовем его х. Если x больше первого элемента, мы оставляем его как есть. Если x меньше, мы копируем значение первого элемента во вторую позицию и затем устанавливаем первый элемент в x.
Когда мы переходим к другим элементам несортированного сегмента, мы непрерывно перемещаем более крупные элементы в отсортированном сегменте вверх по списку, пока не встретим элемент меньше x, или не достигнем конца отсортированного сегмента, а затем поместим x в его правильное положение.
Реализация
Сложность
Сложность сортировки вставками в среднем равна O(n^2).
Пирамидальная сортировка (Heap Sort) (англ. Heapsort, «Сортировка кучей»)
Этот популярный алгоритм сортировки, как сортировки вставками и выбором, сегментирует список на отсортированные и несортированные части. Он преобразует несортированный сегмент списка в структуру данных типа куча (heap), чтобы мы могли эффективно определить самый большой элемент.
Объяснение
Мы начинаем с преобразования списка в Max Heap — бинарное дерево, где самым большим элементом является корневой узел. Затем мы помещаем этот элемент в конец списка. Затем мы восстанавливаем нашу Max Heap, которая теперь имеет на одно меньшее значение, помещая новое наибольшее значение перед последним элементом списка.
Мы повторяем этот процесс построения кучи, пока все узлы не будут удалены.
Реализация
Мы создаем вспомогательную функцию heapify для реализации этого алгоритма:
Сложность
В среднем сложность сортировки кучи составляет O(nlog (n)), что уже значительно быстрее, чем в предыдущих алгоритмах.
Сортировка слиянием (Merge Sort)
Этот алгоритм «разделяй и властвуй» разбивает список пополам и продолжает разбивать список на пары, пока в нем не будут только одиночные элементы.
Соседние элементы становятся отсортированными парами, затем отсортированные пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока мы не получим отсортированный список со всеми элементами несортированного списка.
Объяснение
Мы рекурсивно разделяем список пополам, пока не получим списки с одиночным размером. Затем мы объединяем каждую половину, которая была разделена, и при этом сортируя их.
Сортировка осуществляется путем сравнения наименьших элементов каждой половины. Первый элемент каждого списка сравнивается с первым. Если первая половина начинается с меньшего значения, то мы добавляем ее в отсортированный список. Затем мы сравниваем второе наименьшее значение первой половины с первым наименьшим значением второй половины.
Каждый раз, когда мы выбираем меньшее значение в начале половины, мы перемещаем индекс, элемент которого нужно сравнить на единицу.
Реализация
Обратите внимание, что функция merge_sort(), в отличие от предыдущих алгоритмов сортировки, возвращает новый отсортированный список, а не сортирует существующий список.
Поэтому для сортировки слиянием требуется пространство в памяти для создания нового списка того же размера, что и входной список.
Сложность
В среднем сложность сортировки слиянием составляет O(nlog (n)).
Быстрая сортировка (Quick Sort)
Это то же алгоритм «разделяй и властвуй» и его наиболее часто используют их описанных в этой статье. При правильной настройке он чрезвычайно эффективен и не требует дополнительного пространства памяти как сортировка слиянием. Мы разделяем список вокруг элемента точка опоры, сортируя значения вокруг этой точки.
Объяснение
Быстрая сортировка начинается с разбиения списка — выбора одного значения списка, которое будет в его отсортированном месте. Это значение называется опорным. Все элементы, меньшие, чем этот элемент, перемещаются влево. Все более крупные элементы перемещены вправо.
Зная, что опорный элемент находится на своем правильном месте, мы рекурсивно сортируем значения вокруг этого элемента, пока не будет отсортирован весь список.
Реализация
Сложность
В среднем сложность быстрой сортировки составляет O(nlog (n)).
Примечание. Алгоритм быстрой сортировки будет работать медленно, если опорный элемент будет наименьшим или наибольшим элементом списка. Быстрая сортировка обычно работает быстрее с более сбалансированными значениями. В отличие от сортировки кучи и сортировки слиянием, обе из которых имеют худшие времена O(nlog (n)), быстрая сортировка имеет худшее время O(n^2).
Встроенные функции сортировки Python
Хотя полезно знать и понимать эти алгоритмы сортировки, в большинстве проектов Python вы, вероятно, будете использовать встроенную функцию сортировки.
Создадим новый список, чтобы отсортировать его содержимое с помощью метода sort():
Или мы можем использовать функцию sorted() для создания нового отсортированного списка:
Они оба сортируются в порядке возрастания, но вы можете легко отсортировать в порядке убывания, установив для флага реверса в значение True:
В отличие от созданных нами функций алгоритма сортировки, обе эти функции могут сортировать списки кортежей и классов. Функция sorted() может сортировать любой итеративный объект, который включает в себя — списки, строки, кортежи, словари, наборы (set) и пользовательские итераторы.
Встроенная функция сортировки реализуют алгоритм сортировки Тима. Этот алгоритм, основан на сортировке слиянием и сортировке вставкой.
Сравнение скорости
Чтобы понять, как быстро работают рассмотренные алгоритмы, мы сгенерируем список из 5000 чисел от 0 до 1000. Затем мы определим время, необходимое для завершения каждого алгоритма. Повторим это 10 раз, чтобы мы могли более надежно установить производительность сортировки.
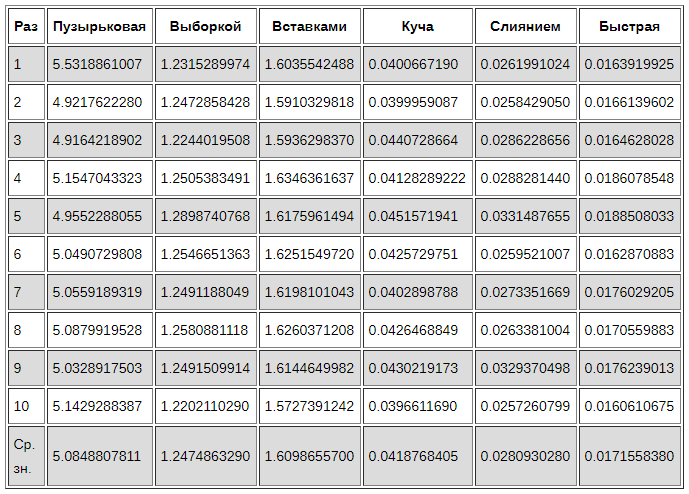
Вот какие результаты мы получили, время в секундах:
| Run | Bubble Пузырьковая | Selection Выбором | Insertion Вставкой | Heap Пирамидальная | Merge Слиянием | Quick Быстрая |
|---|---|---|---|---|---|---|
| 1 | 5.531886100769043 | 1.2315289974212646 | 1.6035542488098145 | 0.04006671905517578 | 0.0261991024017334 | 0.016391992568969727 |
| 2 | 4.921762228012085 | 1.2472858428955078 | 1.5910329818725586 | 0.03999590873718262 | 0.025842905044555664 | 0.01661396026611328 |
| 3 | 4.916421890258789 | 1.2244019508361816 | 1.5936298370361328 | 0.044072866439819336 | 0.028622865676879883 | 0.01646280288696289 |
| 4 | 5.154704332351685 | 1.2505383491516113 | 1.6346361637115479 | 0.04128289222717285 | 0.028828144073486328 | 0.01860785484313965 |
| 5 | 4.955228805541992 | 1.2898740768432617 | 1.61759614944458 | 0.04515719413757324 | 0.033148765563964844 | 0.01885080337524414 |
| 6 | 5.049072980880737 | 1.2546651363372803 | 1.625154972076416 | 0.042572975158691406 | 0.02595210075378418 | 0.01628708839416504 |
| 7 | 5.05591893196106 | 1.2491188049316406 | 1.6198101043701172 | 0.040289878845214844 | 0.027335166931152344 | 0.017602920532226562 |
| 8 | 5.087991952896118 | 1.2580881118774414 | 1.6260371208190918 | 0.04264688491821289 | 0.02633810043334961 | 0.017055988311767578 |
| 9 | 5.032891750335693 | 1.2491509914398193 | 1.6144649982452393 | 0.04302191734313965 | 0.032937049865722656 | 0.0176239013671875 |
| 10 | 5.142928838729858 | 1.2202110290527344 | 1.5727391242980957 | 0.03966116905212402 | 0.0257260799407959 | 0.016061067581176758 |
| Avg | 5.084880781173706 | 1.2474863290786744 | 1.6098655700683593 | 0.04187684059143067 | 0.02809302806854248 | 0.017155838012695313 |
Вы можете получить другие значения, если попробуете повторить тест самостоятельно, но общее соотношение должно быть одинаковым или похожим. Пузырьковая сортировка (Bubble Sort) — самая медленная и наихудшая из всех алгоритмов. Хотя она очень полезно в качестве введения в изучения алгоритмов сортировки, оно не подходит для практического использования.
Мы также заметили, что быстрая сортировка выполняется очень быстро, почти в два раза быстрее, чем сортировка слиянием, и для ее работы не требуется много памяти. Напомним, что наш опорный элемент был основан на среднем элементе списка, разные опорные элементы могут дать разные результаты.
Поскольку сортировка вставкой выполняет намного меньше сравнений, чем сортировка выбором, то обычно она выполняются быстрее, но в нашем тесте сортировка выбором выполнилась немного быстрее.
Сортировка вставкой делает гораздо больше замен, чем сортировка выбором. Скорее всего обмен значениями занял значительно больше времени, чем сравнение значений, поэтому мы получили этот «противоположный» результат.
При выборе алгоритма сортировки следует помнить о самих данных и среде запуска алгоритмов, так как это тоже влияет на производительность.
Заключение
Алгоритмы сортировки дают нам много способов упорядочить наши данные. Мы рассмотрели 6 различных алгоритмов — Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Heap Sort, Quick Sort — и их реализации в Python.
Количество сравнений и перестановок, которые выполняет алгоритм вместе со средой, в которой выполняется код, являются ключевыми определяющими факторами производительности. В реальных приложениях Python рекомендуется придерживаться встроенных функций сортировки Python из-за их гибкости и скорости.