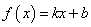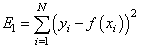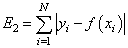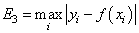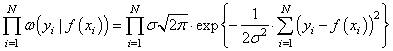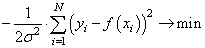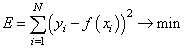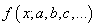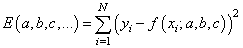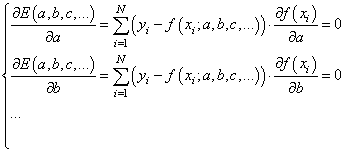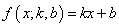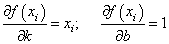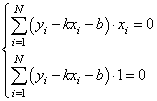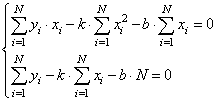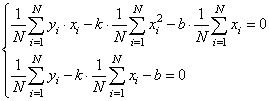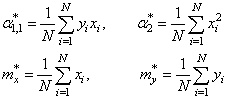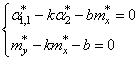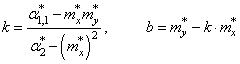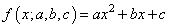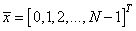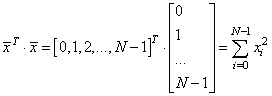аппроксимация в питоне код
Метод наименьших квадратов
На этом занятии мы с вами рассмотрим алгоритм, который носит название метод наименьших квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны базовые знания по теории вероятностей, в частности понимание ПРВ, а также знать, что такое производная и как она вычисляется. Остальное я сейчас расскажу.
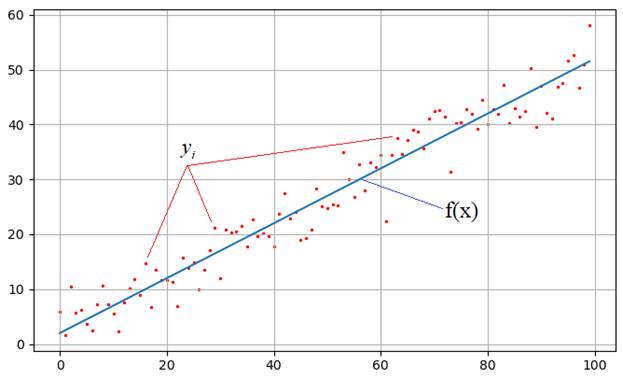
На практике встречаются задачи, когда производились измерения некоторой функциональной зависимости, но из-за погрешностей приборов, или неточных сведений или еще по какой-либо причине, измерения немного отстоят от истинных значений функции и образуют некий разброс:
Наша задача: зная характер функциональной зависимости, подобрать ее параметры так, чтобы она наилучшим образом описывала экспериментальные данные 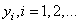
чтобы построить аппроксимацию (приближение) линейного графика к экспериментальным зависимостям. Конечно, вид функциональной зависимости может быть и другим, например, квадратической (парабола), синусоидальной, или даже определяться суммой известных функций, но для простоты понимания, мы для начала рассмотрим именно линейный график с двумя неизвестными коэффициентами.
Итак, будем считать, что на первый вопрос о характере функциональной зависимости экспериментальных данных ответ дан. Следующий вопрос: как измерить качество аппроксимации измерений 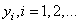
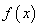
— сумма квадратов ошибок отклонений:
— сумма модулей ошибок отклонений:
— минимум максимальной по модулю ошибки:
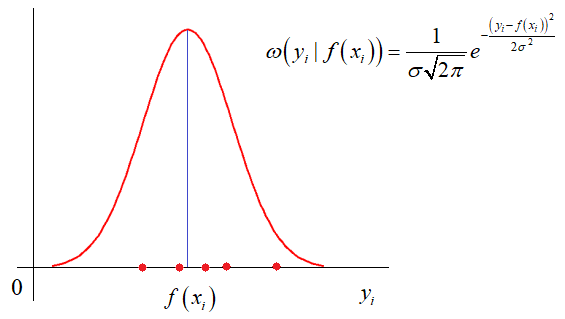
и так далее. Каждый из критериев может приводить к своему алгоритму обработки экспериментальных значений. Так вот, в методе наименьших квадратов используется минимум суммы квадратов ошибок. И этому есть математическое обоснование. Часто результаты реальных измерений имеют стандартное (гауссовское) отклонение относительно измеряемого параметра:
Здесь σ – стандартное отклонение (СКО) наблюдаемых значений 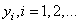
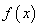
Получается, что лучшее описание экспериментальных данных с помощью функции 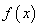
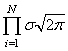
Здесь также множитель можно не учитывать, получаем критерий качества минимум суммы квадрата ошибок:
Как мы помним, наша цель – подобрать параметры 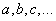
которые как раз и обеспечивают минимум этого критерия, то есть, величина E зависит от этих подбираемых величин:
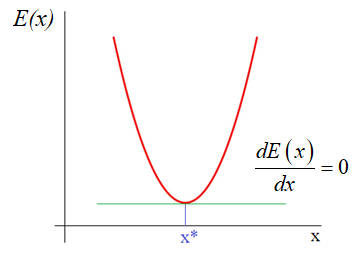
И ее можно рассматривать как квадратическую функцию от аргументов 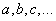
Здесь все также, нужно взять частные производные по каждому параметру и приравнять результат нулю, получим систему линейных уравнений:
Чтобы наполнить конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной функцией:
Эта функция зависит от двух параметров: k и b с частными производными:
Подставляем все в систему, имеем:
Смотрите, что в итоге получилось. Формулы с суммами представляют собой первые и вторые начальные моменты, а также один смешанный момент:
Здесь * означает экспериментальные моменты. В этих обозначениях, получаем:
Отсюда находим, что
Все, мы получили оценки параметров k и b для линейной аппроксимации экспериментальных данных по методу наименьших квадратов. По аналогии можно вычислять параметры для других функциональных зависимостей, например, квадратической:
Здесь будет уже три свободных параметра и три уравнения, решая которые будем получать лучшую аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений.
Реализация на Python
В заключение этого занятия реализуем метод наименьших квадратов на Python. Для этого нам понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас не установлены, то делается это просто – через команды:
pip install matplotlib
После этого, мы можем их импортировать и использовать в программе:
Первая довольно эффективная для выполнения различных математических операций, включая векторные и матричные. Вторая служит для построения графиков.
Итак, вначале определим необходимые начальные величины:
Формируем вспомогательный вектор
с помощью метода array, который возвращает объект-вектор на основе итерируемой функции range:
Затем, вычисляем значения теоретической функции:
и добавляем к ней случайные отклонения для моделирования результатов наблюдений:
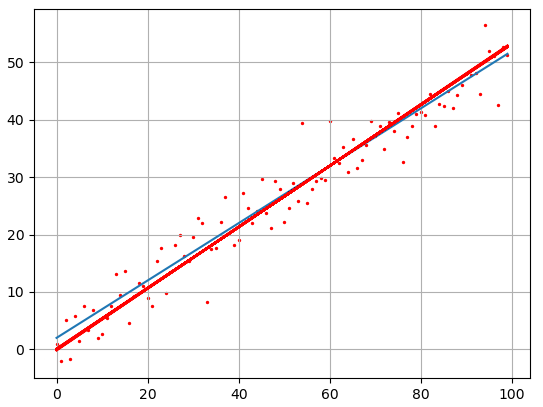
Если сейчас отобразить наборы точек y, то они будут выглядеть следующим образом:
Теперь у нас все есть для вычисления коэффициентов k и b по экспериментальным данным:
Здесь выражение x.T*x – это произведение:
Далее, построим точки полученной аппроксимации:
и отобразим оба линейных графика:
Как видите результат аппроксимации довольно близок начальному, теоретическому графику. Вот так работает метод наименьших квадратов.
Видео по теме
#1: Метод наименьших квадратов
#2: Метод градиентного спуска
#3: Метод градиентного спуска для двух параметров
#4: Марковские процессы в дискретном времени
#5: Фильтр Калмана дискретного времени
#6: Фильтр Калмана для авторегрессионого уравнения
#7: Векторный фильтр Калмана
#9: Байесовское построение оценок, метод максимального правдоподобия
#10: Байесовский классификатор, отношение правдоподобия
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
Сила аппроксимации нейронных сетей (с кодами Python)
Дата публикации Jan 7, 2019
Введение
Хорошо известно, что нейронные сети могут аппроксимировать выходные данные любой непрерывной математической функции, какой бы сложной она ни была. Возьмем, к примеру, функцию ниже:
Хотя он имеет довольно сложную форму, теоремы, которые мы вскоре обсудим, гарантируют, что можно построить некоторую нейронную сеть, которая может приближатьсяF (X)так точно, как мы хотим. Поэтому нейронные сети отображают тип универсального поведения.
Одна из причин, по которой нейронным сетям уделяется так много внимания, заключается в том, что в дополнение к этим довольно замечательным универсальным свойствам,они обладают многими мощными алгоритмами для изучения функций,
Универсальность и основополагающая математика
Эта часть даст неофициальный обзор некоторых фундаментальных математических результатов (теорем), лежащих в основе этих аппроксимационных возможностей искусственных нейронных сетей.
«Практически любой процесс, который вы можете себе представить, можно представить как вычисление функции… [Примеры включают в себя] наименование музыкального произведения на основе короткого образца произведения […], перевод китайского текста на английский […], снятие фильма в формате mp4 файл и генерация описания сюжета фильма, а также обсуждение качества действия ».
Мотивация использования нейронных сетей в качестве аппроксиматоров: теорема Колмогорова
В 1957 году русский математикАндрей Колмогоров, известный своим вкладом в широкий круг математических тем (таких как теория вероятностей, топология, турбулентность, вычислительная сложность и многие другие),доказановажная теорема о представлении вещественных функций многих переменных. Согласно теореме Колмогорова, многомерные функции могут быть выражены через комбинацию сумм и композиций (конечного числа) одномерных функций.
Немного более формально, теорема утверждает, что непрерывная функцияереальных переменных, определенных вNгиперкуб (сN≥ 2) можно представить следующим образом:
Универсальная аппроксимационная теорема (UAT)
UAT утверждает, что нейронные сети с прямой связью, содержащие один скрытый слой с конечным числом узлов, могут использоваться для аппроксимации любой непрерывной функции при условии, что удовлетворяются довольно мягкие предположения о форме функции активации. Теперь, поскольку практически любой процесс, который мы можем себе представить, может быть описан некоторой математической функцией, нейронные сети могут, по крайней мере, в принципе, предсказать результат почти каждого процесса.
Существует несколько строгих доказательств универсальности искусственных нейронных сетей с прямой связью, использующих различные функции активации. Давайте для краткости ограничимся сигмовидной функцией. Сигмоиды имеют S-образную форму и включают в качестве особых случаевлогистическая функция,Кривая Гомперцаикривая ogee,
Python-код для сигмоида
Быстрый код Python для построения и построения сигмоидальной функции:
Доказательство Георгия Цибенко
внутрикомпактныйподмножествоN-мерное реальное пространство и любые положительные ϵ, есть векторы
(веса), константы
(смещениеусловия) и
для любогоИкс(NN входы) внутри компактного подмножества, где функциягдан кем-то:
Выбирая подходящие параметры, нейронные сети могут использоваться для представления функций в широком диапазоне различных форм.
Пример использования Python
Чтобы сделать эти утверждения менее абстрактными, давайте создадим простой код Python, чтобы проиллюстрировать то, что обсуждалось до сих пор. Следующий анализ основан на Майкла Нильсенаотличная онлайн книгаи на исключительных лекцияхМэтт Бремса такжеДжастин ПаундерснаГенеральная Ассамблея Data Science Immersive (DSI),
Мы построим нейронную сеть, чтобы приблизить следующую простую функцию:
Перед погружением в код необходимо сделать несколько замечаний:
Чтобы воспроизвести эту функцию, мы выбираем значениячасs (см. соответствующий рисунок ниже):
Код начинается со следующих определений:
Это приближение далеко от идеала. Однако это просто улучшить, например, путем увеличения количества узлов или количества слоев (но в то же время избегая переоснащения).
Вывод
В этой статье я описал некоторую базовую математику, лежащую в основе универсальных свойств нейронных сетей, и показал простой код Python, который реализует приближение простой функции.
Хотя полный код уже включен в статью, мойGithubи мой личный сайтwww.marcotavora.me(надеюсь) есть еще кое-что интересное как о науке о данных, так и о физике.
Спасибо за чтение и до скорой встречи!
Кстати, конструктивная критика и отзывы всегда приветствуются!
Аппроксимация функции
Добрый день. Помогите, пожалуйста с вот такой задачей по ппроксимации функции
Рассмотрим сложную математическую функцию на отрезке [1, 15]:
f(x) = sin(x / 5) * exp(x / 10) + 5 * exp(-x / 2)
Она может описывать, например, зависимость оценок, которые выставляют определенному сорту вина эксперты, в зависимости от возраста этого вина. По сути, задача машинного обучения состоит в том, чтобы приблизить сложную зависимость с помощью функции из определенного семейства. В этом задании мы будем приближать указанную функцию с помощью многочленов.
Воспользуемся описанным свойством, и будем находить приближение функции многочленом, решая систему линейных уравнений.
Сформируйте систему линейных уравнений (то есть задайте матрицу коэффициентов A и свободный вектор b) для многочлена первой степени, который должен совпадать с функцией f в точках 1 и 15. Решите данную систему с помощью функции scipy.linalg.solve. Нарисуйте функцию f и полученный многочлен. Хорошо ли он приближает исходную функцию?
Повторите те же шаги для многочлена второй степени, который совпадает с функцией f в точках 1, 8 и 15. Улучшилось ли качество аппроксимации?
Повторите те же шаги для многочлена третьей степени, который совпадает с функцией f в точках 1, 4, 10 и 15. Хорошо ли он аппроксимирует функцию? Коэффициенты данного многочлена (четыре числа в следующем порядке: w_0, w_1, w_2, w_3) являются ответом на задачу. Округлять коэффициенты не обязательно, но при желании можете произвести округление до второго знака (т.е. до числа вида 0.42)
Помощь в написании контрольных, курсовых и дипломных работ здесь.
SciPy, оптимизация
SciPy (произносится как сай пай) — это пакет прикладных математических процедур, основанный на расширении Numpy Python. С SciPy интерактивный сеанс Python превращается в такую же полноценную среду обработки данных и прототипирования сложных систем, как MATLAB, IDL, Octave, R-Lab и SciLab. Сегодня я хочу коротко рассказать о том, как следует применять некоторые известные алгоритмы оптимизации в пакете scipy.optimize. Более подробную и актуальную справку по применению функций всегда можно получить с помощью команды help() или с помощью Shift+Tab.
Введение
Дабы избавить самого себя и читателей от поиска и чтения первоисточников, ссылки на описания методов будут в основном на википедию. Как правило, этой информации достаточно для понимания методов в общих чертах и условий их применения. Для понимания сути математических методов идем по ссылкам на более авторитетные публикации, которые можно найти в конце каждой статьи или в любимой поисковой системе.
Итак, модуль scipy.optimize включает в себя реализацию следующих процедур:
В этой статье мы рассмотрим только первый пункт из всего этого списка.
Безусловная минимизация скалярной функции нескольких переменных
Функция minim из пакета scipy.optimize предоставляет общий интерфейс для решения задач условной и безусловной минимизации скалярных функций нескольких переменных. Чтобы продемонстрировать ее работу, нам понадобится подходящая функция нескольких переменных, которую мы будем по-разному минимизировать.
Для этих целей прекрасно подойдет функция Розенброка от N переменных, которая имеет вид:
Несмотря на то, что функция Розенброка и ее матрицы Якоби и Гессе (первой и второй производной соответственно) уже определены в пакете scipy.optimize, определим ее самостоятельно.
Для наглядности отрисуем в 3D значения функции Розенброка от двух переменных.
Зная заранее, что минимум равен 0 при , рассмотрим примеры того, как определить минимальное значение функции Розенброка с помощью различных процедур scipy.optimize.
Симплекс-метод Нелдера-Мида (Nelder-Mead)
Пусть имеется начальная точка x0 в 5-мерном пространстве. Найдем ближайшую к ней точку минимума функции Розенброка с помощью алгоритма симплекса Nelder-Mead (алгоритм указан в качестве значения параметра method):
Симплекс-метод является самым простым способом свести к минимуму явно определенную и довольно гладкую функцию. Он не требует вычисления производных функции, достаточно задать только ее значения. Метод Нелдера-Мида является хорошим выбором для простых задач минимизации. Однако, поскольку он не использует оценки градиента, для поиска минимума может потребоваться больше времени.
Метод Пауэлла
Другим алгоритмом оптимизации, в котором вычисляются только значения функций, является метод Пауэлла. Чтобы использовать его, нужно установить method = ‘powell’ в функции minim.
Алгоритм Бройдена-Флетчера-Голдфарба-Шанно (BFGS)
Для получения более быстрой сходимости к решению, процедура BFGS использует градиент целевой функции. Градиент может быть задан в виде функции или вычисляться с помощью разностей первого порядка. В любом случае, обычно метод BFGS требует меньше вызовов функций, чем симплекс-метод.
Найдем производную от функции Розенброка в аналитическом виде:
Это выражение справедливо для производных всех переменных, кроме первой и последней, которые определяются как:
Посмотрим на функцию Python, которая вычисляет этот градиент:
Функция вычисления градиента указывается в качестве значения параметра jac функции minim, как показано ниже.
Алгоритм сопряженных градиентов (Ньютона)
Алгоритм сопряженных градиентов Ньютона является модифицированным методом Ньютона.
Метод Ньютона основан на аппроксимации функции в локальной области полиномом второй степени:
где является матрицей вторых производных (матрица Гессе, гессиан).
Если гессиан положительно определен, то локальный минимум этой функции можно найти, приравняв нулевой градиент квадратичной формы к нулю. В результате получится выражение:
Обратный гессиан вычисляется с помощью метода сопряженных градиентов. Пример использования этого метода для минимизации функции Розенброка приведен ниже. Чтобы использовать метод Newton-CG, необходимо задать функцию, которая вычисляет гессиан.
Гессиан функции Розенброка в аналитическом виде равен:
где и
, определяют матрицу
.
Остальные ненулевые элементы матрицы равны:
Например, в пятимерном пространстве N = 5, матрица Гессе для функции Розенброка имеет ленточный вид:
Код, который вычисляет этот гессиан вместе с кодом для минимизации функции Розенброка с помощью метода сопряженных градиентов (Ньютона):
Пример с определением функции произведения гессиана и произвольного вектора
В реальных задачах вычисление и хранение всей матрицы Гессе может потребовать значительных ресурсов времени и памяти. При этом фактически нет необходимости задавать саму матрицу Гессе, т.к. для процедуры минимизации нужен только вектор, равный произведению гессиана с другим произвольным вектором. Таким образом, с вычислительной точки зрения намного предпочтительней сразу определить функцию, которая возвращает результат произведения гессиана с произвольным вектором.
Рассмотрим функцию hess, которая принимает вектор минимизации в качестве первого аргумента, а произвольный вектор — как второй аргумент (наряду с другими аргументами минимизируемой функции). В нашем случае вычислить произведение гессиана функции Розенброка с произвольным вектором не очень сложно. Если p — произвольный вектор, то произведение имеет вид:
Функция, вычисляющая произведение гессиана и произвольного вектора, передается как значение аргумента hessp функции minimize:
Алгоритм доверительной области (trust region) сопряженных градиентов (Ньютона)
Плохая обусловленность матрицы Гессе и неверные направления поиска могут привести к тому, что алгоритм сопряженных градиентов Ньютона может быть неэффективным. В таких случаях предпочтение отдается методу доверительной области (trust-region) сопряженных градиентов Ньютона.
Пример с определением матрицы Гессе:
Пример с функцией произведения гессиана и произвольного вектора:
Методы Крыловского типа
Подобно методу trust-ncg, методы Крыловского типа хорошо подходят для решения крупномасштабных задач, поскольку в них используется только матрично-векторные произведения. Их суть в решении задачи в доверительной области, ограниченной усеченным подпространством Крылова. Для неопределенных задач лучше использовать этот метод, так как он использует меньшее количество нелинейных итераций за счет меньшего количества матрично-векторных произведений на одну подзадачу, по сравнению с методом trust-ncg. Кроме того, решение квадратичной подзадачи находится более точно, чем методом trust-ncg.
Пример с определением матрицы Гессе:
Пример с функцией произведения гессиана и произвольного вектора:
Алгоритм приближенного решения в доверительной области
Все методы (Newton-CG, trust-ncg и trust-krylov) хорошо подходят для решения крупномасштабных задач (с тысячами переменных). Это связано с тем, что лежащий в их основе алгоритм сопряженных градиентов подразумевает приближенное нахождение обратной матрицы Гессе. Решение находится итеративно, без явного разложения гессиана. Поскольку требуется определить только функцию для произведение гессиана и произвольного вектора, этот алгоритм особенно хорош для работы с разреженными (ленточными диагональными) матрицами. Это обеспечивает низкие затраты памяти и значительную экономию времени.
В задачах среднего размера затраты на хранение и факторизацию гессиана не имеют решающего значения. Это значит, что можно получить решение за меньшее количество итераций, разрешив подзадачи области доверия почти точно. Для этого некоторые нелинейные уравнения решаются итеративно для каждой квадратичной подзадачи. Такое решение требует обычно 3 или 4 разложения Холецкого матрицы Гессе. В результате метод сходится за меньшее количество итераций и требует меньше вычислений целевой функции, чем другие реализованные методы доверительной области. Этот алгоритм подразумевает только определение полной матрицы Гессе и не поддерживает возможность использовать функцию произведения гессиана и произвольного вектора.