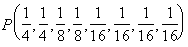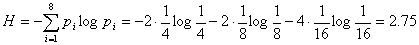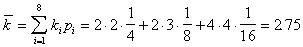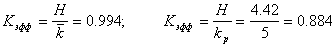алгоритм построения кода шеннона фано
Код Шеннона
Код Шеннона — алгоритм префиксного кодирования алфавита, предложенный Клодом Шенноном, в котором используется избыточность сообщения, заключённая в неоднородном распределении частот символов первичного алфавита, то есть заменяет коды более частых символов короткими последовательностями, а коды более редких символов — более длинными последовательностями.
называется кодом Шеннона.
Содержание
Алгоритм построения бинарного кода Шеннона [ править ]
Пример [ править ]
Для примера возьмём алфавит [math]A=\
| Символ | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| [math]p_ | 0.10 | 0.20 | 0.10 | 0.10 | 0.35 | 0.15 |
По алгоритму сортируем элементы алфавита по не возрастанию [math]p_
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| [math]p_ | 0.35 | 0.20 | 0.15 | 0.10 | 0.10 | 0.10 |
Каждому символу [math]a_
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| [math]b_ | 0.00 | 0.35 | 0.55 | 0.70 | 0.80 | 0.90 |
Переведём [math]b_
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| [math]b_ | 0.00000 | 0.01010 | 0.10001 | 0.10110 | 0.11001 | 0.11100 |
Посчитаем [math]L_
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| [math]L_ | 2 | 3 | 3 | 4 | 4 | 4 |
| Код | 00 | 010 | 100 | 1011 | 1100 | 1110 |
| Утверждение: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
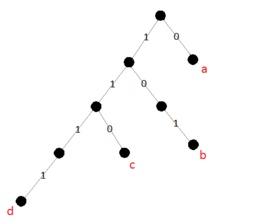
| Символ | a | b | c | d |
|---|---|---|---|---|
| [math]p_ | 0.65 | 0.15 | 0.15 | 0.05 |
| [math]b_ | 0 | 0.65 | 0.80 | 0.95 |
| [math]L_ | 1 | 3 | 3 | 5 |
| Код | 0 | 101 | 110 | 1111 |
Изобразим полученный результат в виде кодового дерева. Из этого рисунка видно, что полученные кодовые слова для букв [math]d[/math] и [math]b[/math] не являются оптимальными, так как их можно сократить на один бит без потери свойства однозначной декодируемости. Поэтому более эффективным считается сжатие метод Хаффмана.
Алгоритм вычисления кодов Шеннона-Фано



Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем.
Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий.
Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
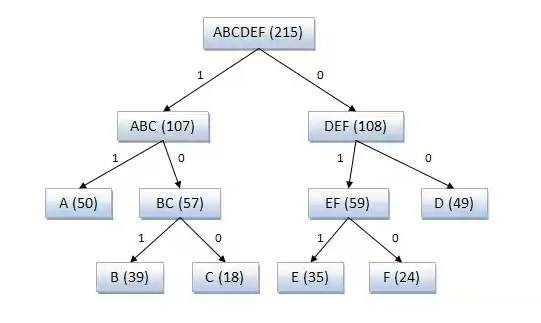
Пример кодового дерева
Исходные символы:
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона-Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример 1. Закодируем буквы алфавита в коде Шеннона-Фано.
Пусть имеется случайная величина X (x1, x2, x3, x4, x5, x6, x7, x8), имеющая восемь состояний с распределением вероятностей
Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:
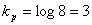
Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию
Определив избыточность L по формуле L=1-H/H0=1-2,75/3=0,084, видим, что возможно сокращение длины кода на 8,4%.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)
| X | P | Коды | |
| x1 | 1/4 | ——- | ——- |
| x2 | 1/4 | ——- | ——- |
| x3, | 1/8 | ——- | |
| x4 | 1/8 | ——- | |
| x5 | 1/16 | ||
| x6 | 1/16 | ||
| x7 | 1/16 | ||
| x8 | 1/16 |
Средняя длина полученного кода будет равна
Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы.
Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице
| Буква | Рi | Код | ||
| ? | 0.145 | — | ||
| о | 0.095 | — | ||
| е | 0.074 | |||
| а | 0.064 | |||
| и | 0.064 | |||
| н | 0.056 | |||
| т | 0.056 | … | … | — |
| с | 0.047 | … | … | |
| . | … | |||
| ф | 0.03 |
Средняя длина данного кода будет равна, 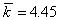
Энтропия H=4.42 бит/буква. Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины 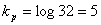
Код Шеннона-Фано
Алгоритм Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона-Фано префиксные, то есть, никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.
Содержание
Основные сведения
Кодирование Шеннона-Фано (англ. Shannon-Fano coding) — алгоритм префиксного неоднородного кодирования. Относится к вероятностным методам сжатия (точнее, методам контекстного моделирования нулевого порядка). Подобно алгоритму Хаффмана алгоритм Шеннона-Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями.
Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).
Основные этапы
Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей p0 − p1 может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность, большую нуля).
Алгоритм вычисления кодов Шеннона-Фано
Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Все множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n+1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути еше не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева
A (частота встречаемости 50), B (частота встречаемости 39), C (частота встречаемости 18), D (частота встречаемости 49), E (частота встречаемости 35), F (частота встречаемости 24).
A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина сжатой последовательности, по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются неоптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным.
Литература
Ссылки
Методы сжатия
| Информация | Собственная · Взаимная · Энтропия · Условная энтропия · Сложность · Избыточность |
|---|---|
| Единицы измерения | Бит · Нат · Ниббл · Хартли · Формула Хартли |
| Энтропийное сжатие | Алгоритм Хаффмана · Адаптивный алгоритм Хаффмана · Арифметическое кодирование ( Алгоритм Шеннона — Фано · Интервальное) · Коды Голомба · Дельта · Универсальный код (Элиаса · Фибоначчи) |
|---|---|
| Словарные методы | RLE · · LZ ( · LZSS · LZW · LZWL · · · LZX · LZRW · LZJB · LZT) |
| Прочее | RLE · CTW · BWT · PPM · DMC |
| Теория | Свёртка · PCM · Алиасинг · Дискретизация · Теорема Котельникова |
|---|---|
| Методы | LPC (LAR · LSP) · WLPC · CELP · ACELP · A-закон · μ-закон · MDCT · Преобразование Фурье · Психоакустическая модель |
| Прочее | Dynamic range compression · Сжатие речи · Полосное кодирование |
| Термины | Цветовое пространство · Пиксел · Chroma subsampling · Артефакты сжатия |
|---|---|
| Методы | RLE · DPCM · Фрактальный · Wavelet · EZW · SPIHT · LP · ДКП · ПКЛ |
| Прочее | Битрейт · Test images · PSNR · Квантование |
| Термины | Характеристики видео · Кадр · Типы кадров · Качество видео |
|---|---|
| Методы | Компенсация движения · ДКП · Квантование |
| Прочее | Видеокодек · Rate distortion theory (CBR · ABR · VBR) |
Полезное
Смотреть что такое «Код Шеннона-Фано» в других словарях:
Алгоритм Шеннона — Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет … Википедия
Кодирование Шеннона-Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм… … Википедия
Код — У этого термина существуют и другие значения, см. Код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется отдельная… … Википедия
Код Хаффмена — Алгоритм Хаффмана (англ. Huffman) адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. В настоящее… … Википедия
Код Хаффмана — Алгоритм Хаффмана адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им … Википедия
Шеннона теорема — Теорема Котельникова (в англоязычной литературе теорема Найквиста) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой более… … Википедия
Алгоритм Шеннона — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Robert Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на… … Википедия
Прямая теорема Шеннона для канала без помех — Не следует путать с другими теоремами Шеннона. Теоремы Шеннона для источника общего вида описывают возможности кодирования источника общего вида с помощью разделимых кодов. Другими словами, описываются максимально достижимые возможности… … Википедия
Теоремы Шеннона для источника общего вида — Не следует путать с другими теоремами Шеннона. Теоремы Шеннона для источника общего вида описывают возможности кодирования источника общего вида с помощью разделимых кодов. Другими словами, описываются максимально достижимые возможности… … Википедия
Прямая теорема Шеннона для источника общего вида — Не следует путать с другими теоремами Шеннона. Теоремы Шеннона для источника общего вида описывают возможности кодирования источника общего вида с помощью разделимых кодов. Другими словами, описываются максимально достижимые возможности… … Википедия
Кодирование Шеннона-Фано
Алгоритм Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона-Фано префиксные, то есть, никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.
Содержание
Основные сведения
Кодирование Шеннона-Фано (англ. Shannon-Fano coding) — алгоритм префиксного неоднородного кодирования. Относится к вероятностным методам сжатия (точнее, методам контекстного моделирования нулевого порядка). Подобно алгоритму Хаффмана алгоритм Шеннона-Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями.
Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).
Основные этапы
Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей p0 − p1 может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность, большую нуля).
Алгоритм вычисления кодов Шеннона-Фано
Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Все множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n+1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути еше не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева
A (частота встречаемости 50), B (частота встречаемости 39), C (частота встречаемости 18), D (частота встречаемости 49), E (частота встречаемости 35), F (частота встречаемости 24).
A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина сжатой последовательности, по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются неоптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным.
Литература
Ссылки
Методы сжатия
| Информация | Собственная · Взаимная · Энтропия · Условная энтропия · Сложность · Избыточность |
|---|---|
| Единицы измерения | Бит · Нат · Ниббл · Хартли · Формула Хартли |
| Энтропийное сжатие | Алгоритм Хаффмана · Адаптивный алгоритм Хаффмана · Арифметическое кодирование ( Алгоритм Шеннона — Фано · Интервальное) · Коды Голомба · Дельта · Универсальный код (Элиаса · Фибоначчи) |
|---|---|
| Словарные методы | RLE · · LZ ( · LZSS · LZW · LZWL · · · LZX · LZRW · LZJB · LZT) |
| Прочее | RLE · CTW · BWT · PPM · DMC |
| Теория | Свёртка · PCM · Алиасинг · Дискретизация · Теорема Котельникова |
|---|---|
| Методы | LPC (LAR · LSP) · WLPC · CELP · ACELP · A-закон · μ-закон · MDCT · Преобразование Фурье · Психоакустическая модель |
| Прочее | Dynamic range compression · Сжатие речи · Полосное кодирование |
| Термины | Цветовое пространство · Пиксел · Chroma subsampling · Артефакты сжатия |
|---|---|
| Методы | RLE · DPCM · Фрактальный · Wavelet · EZW · SPIHT · LP · ДКП · ПКЛ |
| Прочее | Битрейт · Test images · PSNR · Квантование |
| Термины | Характеристики видео · Кадр · Типы кадров · Качество видео |
|---|---|
| Методы | Компенсация движения · ДКП · Квантование |
| Прочее | Видеокодек · Rate distortion theory (CBR · ABR · VBR) |
Смотреть что такое «Кодирование Шеннона-Фано» в других словарях:
Алгоритм Шеннона — Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет … Википедия
Код Шеннона-Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм… … Википедия
Кодирование энтропии — кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых… … Википедия
Кодирование с минимальной избыточностью — Кодирование энтропии кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных… … Википедия
Кодирование длин серий — (англ. Run length encoding, RLE) или Кодирование повторов простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд. При кодировании… … Википедия
Кодирование Хаффмана — Алгоритм Хаффмана (англ. Huffman) адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. В настоящее… … Википедия
Шеннона теорема — Теорема Котельникова (в англоязычной литературе теорема Найквиста) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой более… … Википедия
Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия
Алгоритм Шеннона — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Robert Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на… … Википедия
Энтропийное кодирование — Для термина «Кодирование» см. другие значения. Энтропийное кодирование кодирование последовательности значений с возможностью однозначного восстановления с целью уменьшения объёма данных (длины последовательности) с помощью усреднения… … Википедия