8 биттен тратын код
Бит | Байт | Системы счисления
Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.
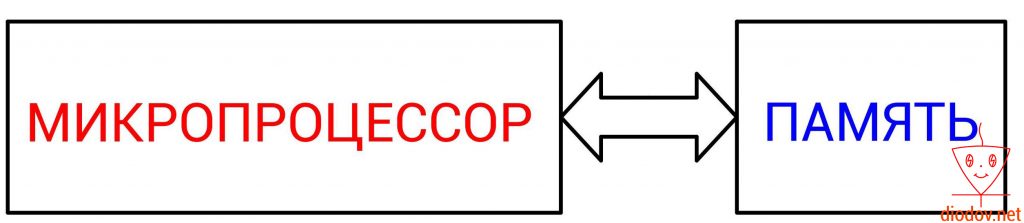
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.
Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.
Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.
Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.
Десятичная система счисления
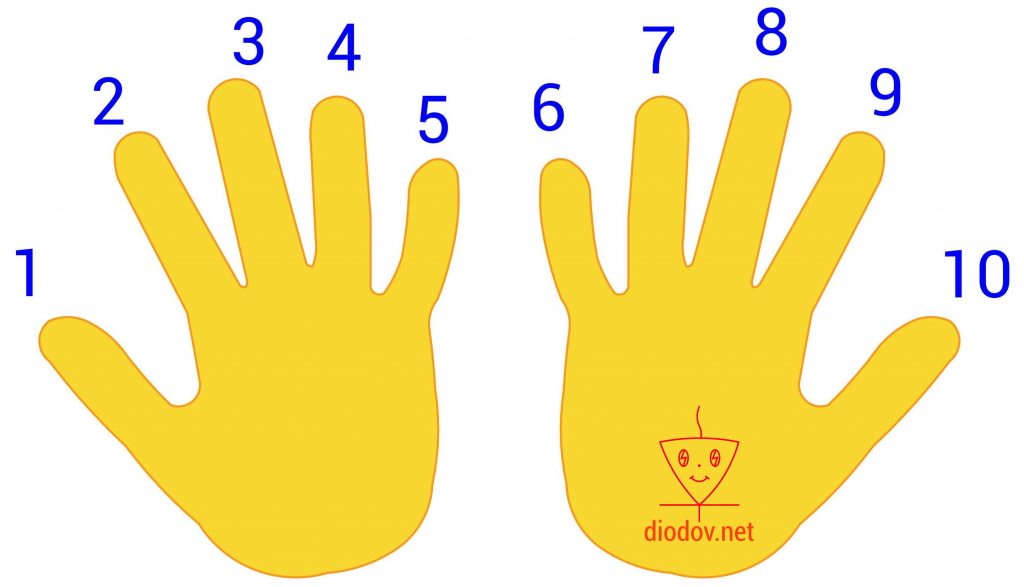
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.
Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.
Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.
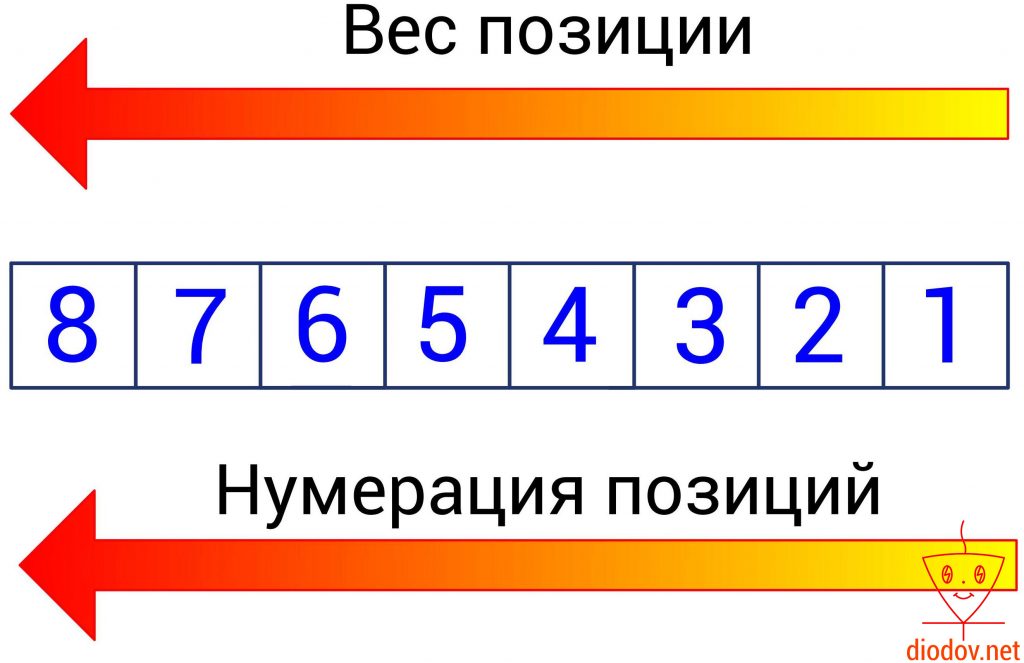
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.
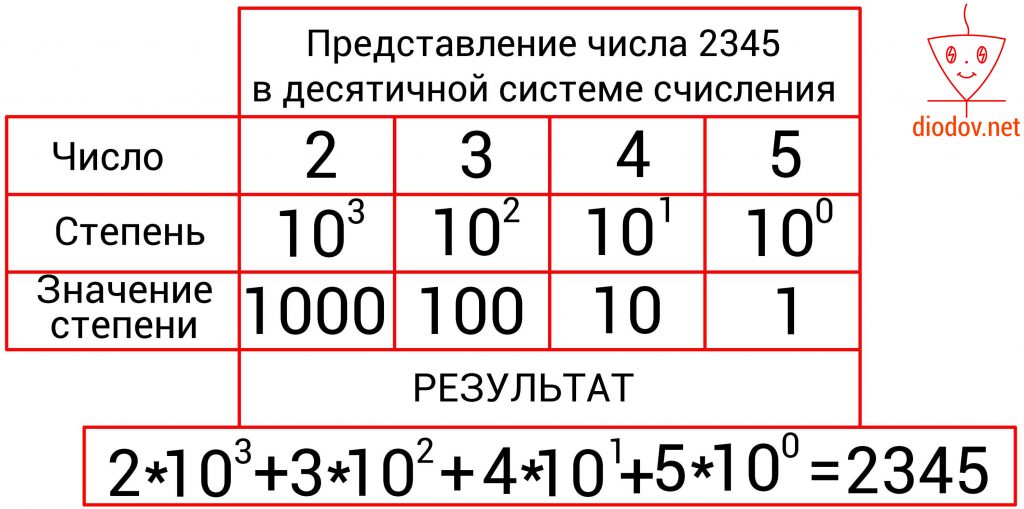
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.
Двоичная система счисления
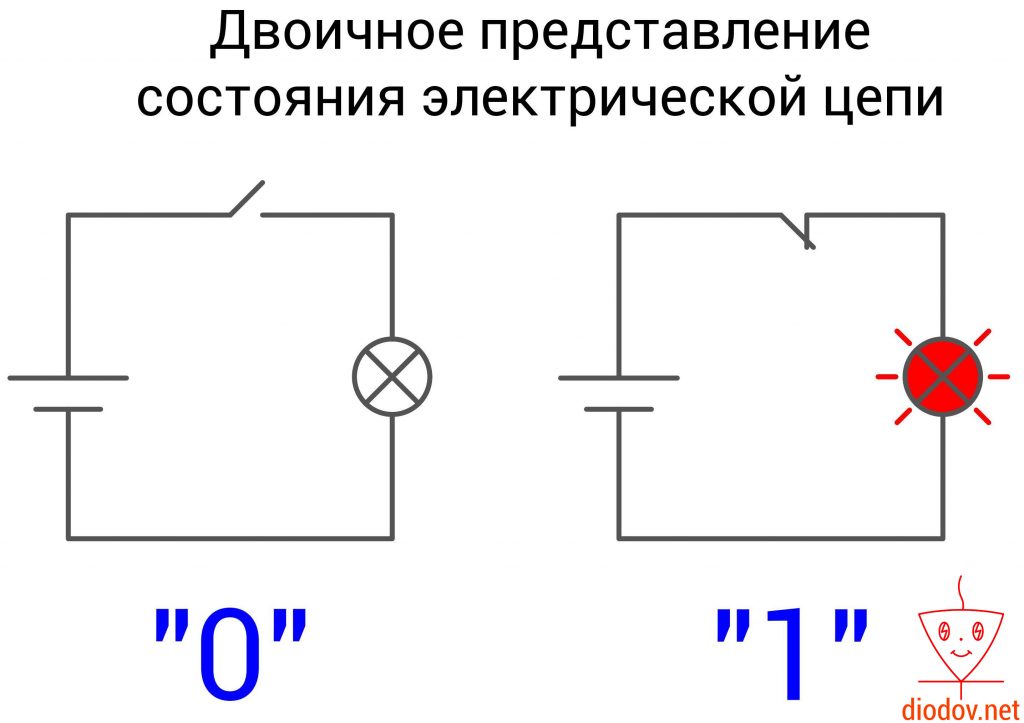
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.
Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.
Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:
110110 – десятичное.
При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.
0b11010101 – двоичное;
11010101 – десятичное.
Бит и байт
Двоичная система счисления также используется при хранении и обработке информации.
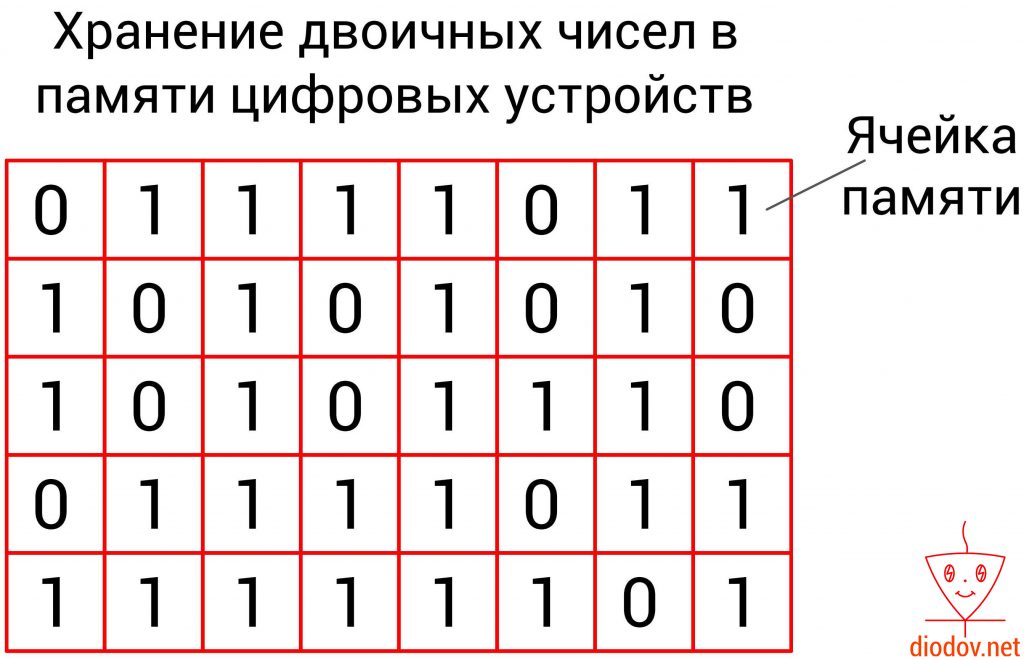
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.
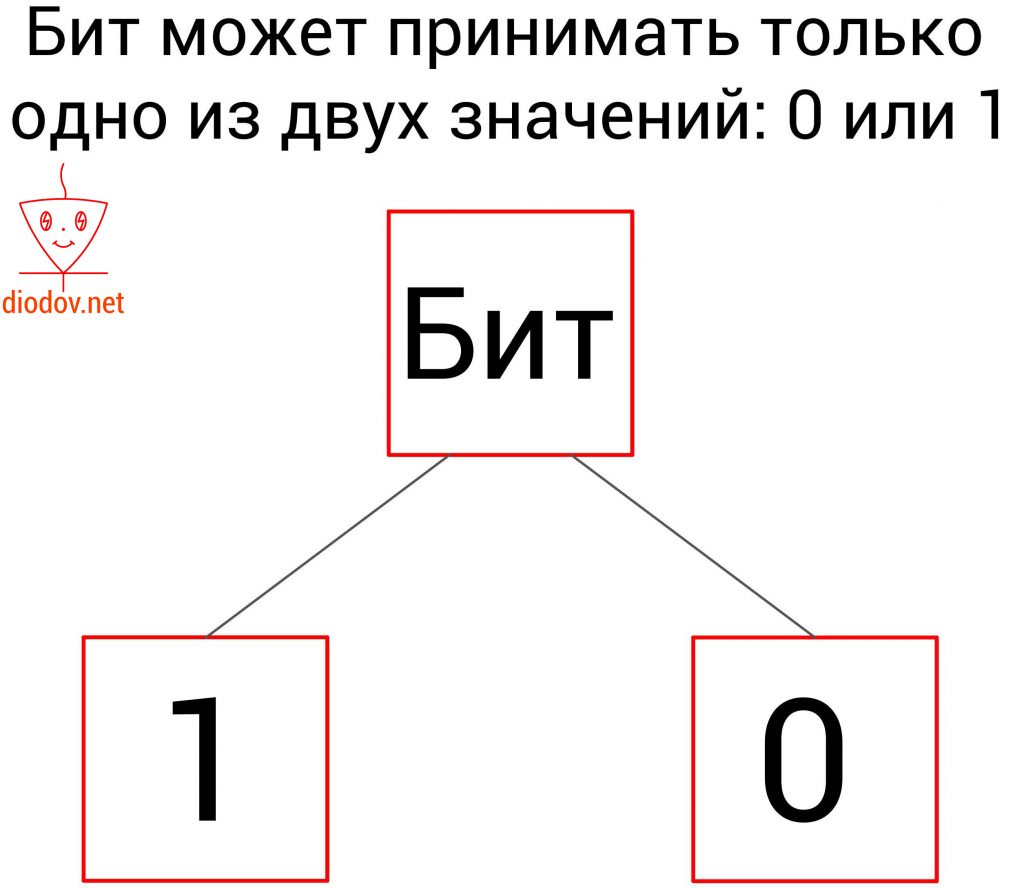
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.
Bit происходит от двух английских слов Binary Digit (двоичное число).
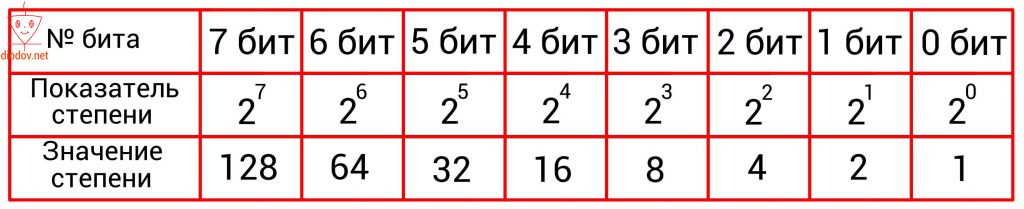
При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.
Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.
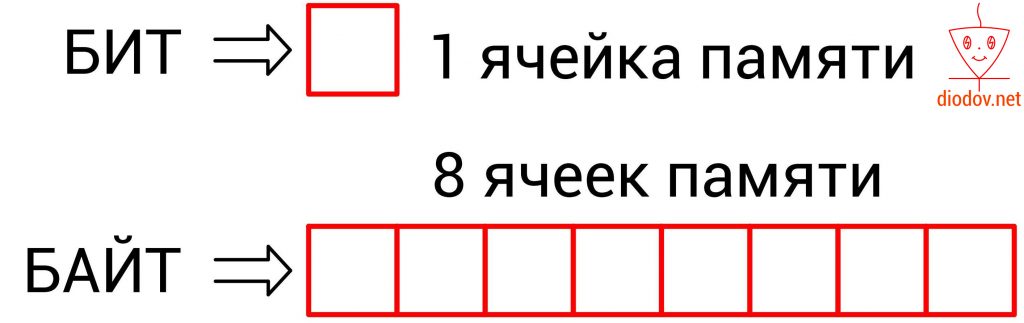
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.
1 байт = 8 бит
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.
На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.
1 килобайт (кБ) = 1024 байт
1 мегабайт (МБ) = 1024 кБ
1 гигабайт (ГБ) = 1024 МБ
1 терабайт (ТБ) = 1024 ГБ
Преобразование десятичного числа в двоичное
На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.
Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.
Теперь давайте переведем число 125 в двоичную форму.
125/2 = 62 остаток 1
Получаем двоичное число 11111012
Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.
Второй способ
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.
Давайте преобразуем 125.
Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.
Преобразование двоичного числа в десятичное
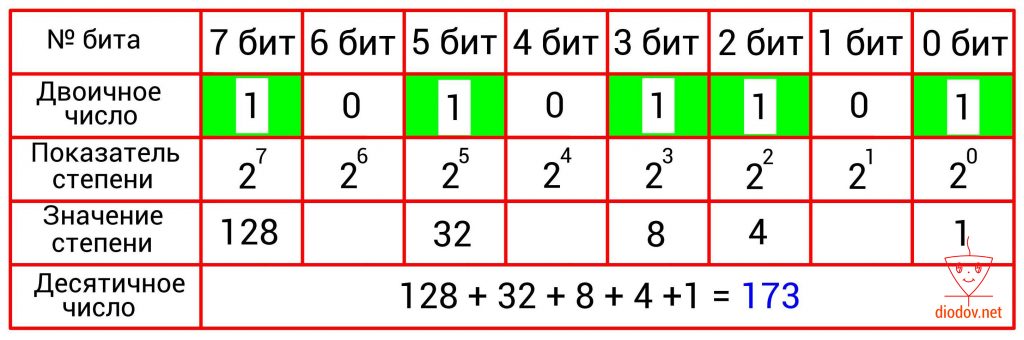
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.
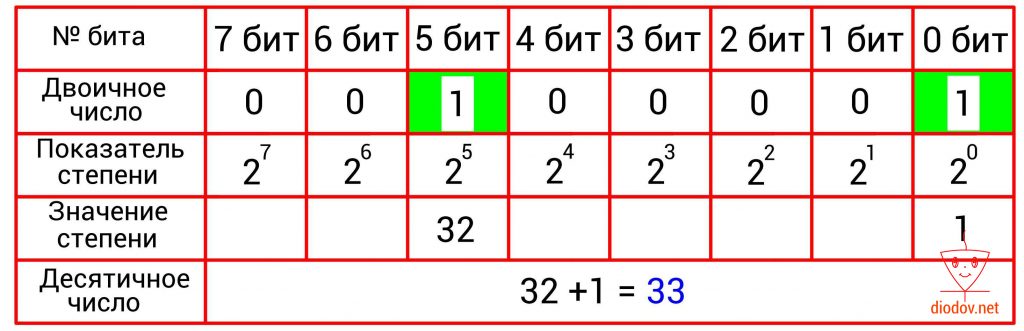
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.
Шестнадцатеричная система счисления
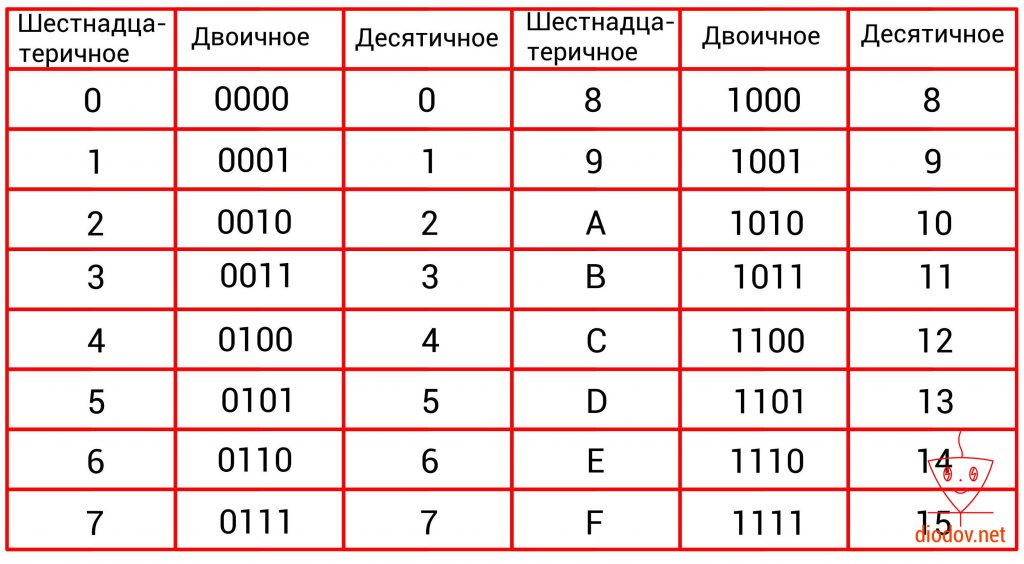
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 10010 или 7 двоичных разрядов 11001002 и только 2 шестнадцатеричных разряда 6416.
А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:
1 000 00010 = 1111 0100 0010 0100 00002 = F424016
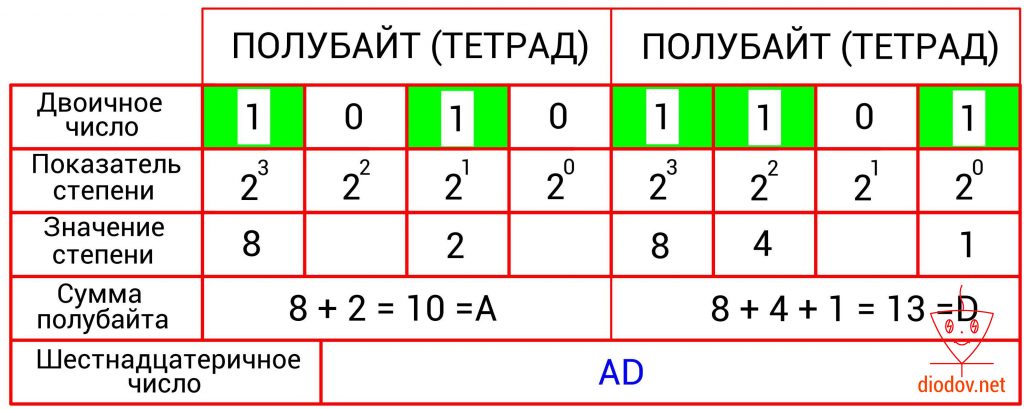
Преобразование двоичного числа в шестнадцатеричное
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.
Другие системы счисления
В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.
Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.
Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.
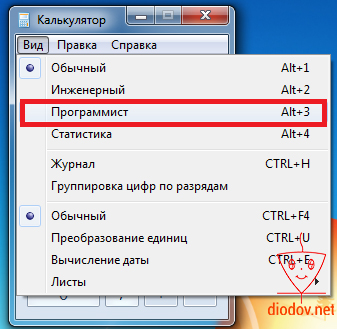
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.
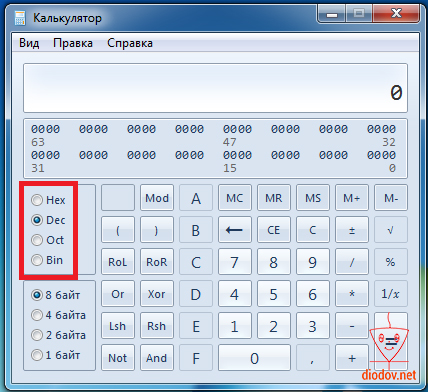
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.
В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)
Обстоятельно о подсчёте единичных битов
Я хотел бы подарить сообществу Хабра статью, в которой стараюсь дать достаточно полное описание подходов к алгоритмам подсчёта единичных битов в переменных размером от 8 до 64 битов. Эти алгоритмы относятся к разделу так называемой «битовой магии» или «битовой алхимии», которая завораживает своей красотой и неочевидностью многих программистов. Я хочу показать, что в основах этой алхимии нет ничего сложного, и вы даже сможете разработать собственные методы подсчёта единичных битов, познакомившись с фундаментальными приёмами, составляющими подобные алгоритмы.
Прежде чем мы начнём, я сразу хочу предупредить, что это статья не для новичков в программировании. Мне необходимо, чтобы читатель в общих чертах представлял себе простейшие битовые операции (побитовое «и», «или», сдвиг), хорошо владел шестнадцатеричной системой счисления и достаточно уверенно пользовался воображением, представляя в нём не всегда короткие битовые последовательности. По возможности, всё будет сопровождаться картинками, но сами понимаете, они лишь упрощают, но не заменяют полное представление.
Все описанные приёмы были реализованы на языке Си и протестированы в двух режимах: 32 и 64 бита. Таким образом, для более полного понимания статьи будет лучше, чтобы вы хотя бы приблизительно понимали язык Си. Тестирование проходило на процессоре Core 2 Duo E8400 @3GHz на 64-х битовой Windows 7. Измерение чистого времени работы программ проводилось с помощью утилиты runexe. Все исходные коды описываемых алгоритмов доступны в архиве на Яндекс диске, их компиляция проверена для компиляторов Visual C++, Intel C++, GCC и CLang, так что в принципе, проблем у вас быть не должно, если кто-то захочет перепроверить результаты у себя. Пользователи Linux, думаю, лучше меня знают, как им тестировать время работы программы у себя в системе, поэтому им советов не даю.
Среди читателей, возможно, будут такие, кому проще посмотреть всё то же самое на видео. Я записал такое видео (58 минут), в котором в формате презентации изложено в точности всё то же самое, что будет ниже по тексту, но может немного в другом стиле, более сухо и строго, тогда как текст я попытался немного оживить. Поэтому изучайте материал так, как кому удобнее.
Сейчас будут последовательно описаны алгоритмы, порождаемые тем или иным набором алхимических приёмов, в каждом разделе будет таблица сравнения времени работы для переменных разного размера, а в конце будет сводная таблица по всем алгоритмам. Во всех алгоритмах используются псевдонимы для чисел без знака от 8 до 64 бит.
Наивный подход
Очевидно, что битовая алхимия применяется вовсе не для того, чтобы блистать на собеседовании, а с целью существенного ускорения программ. Ускорения по отношению к чему? По отношению к тривиальным приёмам, которые могут прийти в голову, когда нет времени более детально вникнуть в задачу. Таковым приёмом и является наивный подход к подсчёту битов: мы просто «откусываем» от числа один бит за другим и суммируем их, повторяя процедуру до тех пор, пока число не станет равным нулю.
Я не вижу смысла что-либо комментировать в этом тривиальном цикле. Невооружённым взглядом ясно, что если старший бит числа n равен 1, то цикл вынужден будет пройтись по всем битам числа, прежде чем доберётся до старшего.
Меняя тип входного параметра u8 на u16, u32 и u64 мы получим 4 различные функции. Давайте протестируем каждую из них на потоке из 2 32 чисел, подаваемых в хаотичном порядке. Понятно, что для u8 у нас 256 различных входных данных, но для единообразия мы всё равно прогоняем 2 32 случайных чисел для всех этих и всех последующих функций, причём всегда в одном и том же порядке (за подробностями можно обратиться к коду учебной программы из архива).
Время в таблице ниже указано в секундах. Для тестирования программа запускалась трижды и выбиралось среднее время. Погрешность едва ли превышает 0,1 секунды. Первый столбец отражает режим компилятора (32-х битовый исходный код или 64-х битовый), далее 4 столбца отвечают за 4 варианта входных данных.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 38,18 | 72,00 | 130,49 | 384,76 |
| x64 | 37,72 | 71,51 | 131,47 | 227,46 |
Как мы видим, скорость работы вполне закономерно возрастает с ростом размера входного параметра. Немного выбивается из общей закономерности вариант, когда числа имеют размер 64 бита, а подсчёт идёт режиме x86. Ясное дело, что процессор вынужден делать четырёхкратную работу при удвоении входного параметра и даже хорошо, что он справляется всего лишь втрое медленнее.
Первая польза этого подхода в том, что при его реализации трудно ошибиться, поэтому написанная таким образом программа может стать эталонной для проверки более сложных алгоритмов (именно так и было сделано в моём случае). Вторая польза в универсальности и относительно простой переносимости на числа любого размера.
Трюк с «откусыванием» младших единичных битов
Этот алхимический приём основан на идее обнуления младшего единичного бита. Имея число n, мы можем произнести заклинание n=n&(n-1), забирая у числа n его младшую единичку. Картинка ниже для n=232 прояснит ситуацию для людей, впервые узнавших об этом трюке.
Код программы не сильно изменился.
Теперь цикл выполнится ровно столько раз, сколько единиц в числе n. Это не избавляет от худшего случая, когда все биты в числе единичные, но значительно сокращает среднее число итераций. Сильно ли данный подход облегчит страдания процессора? На самом деле не очень, а для 8 бит будет даже хуже. Напомню, что сводная таблица результатов будет в конце, а здесь в каждом разделе будет своя таблица.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 44,73 | 55,88 | 72,02 | 300,78 |
| x64 | 40,96 | 69,16 | 79,13 | 126,72 |
Предподсчёт
Не будем торопиться переходить к «жёстким» заклинаниям, рассмотрим последний простой приём, который может спасти даже самого неопытного мага. Данный вариант решения задачи не относится напрямую к битовой алхимии, однако для полноты картины должен быть рассмотрен в обязательном порядке. Заведём две таблицы на 256 и 65536 значений, в которых заранее посчитаны ответы для всех возможных 1-байтовых и 2-байтовых величин соответственно.
Теперь программа для 1 байта будет выглядеть так
Чтобы рассчитать число бит в более крупных по размеру числах, их нужно разбить на байты. Например, для u32 может быть вот такой код:
Или такой, если мы применяем таблицу предподсчёта для 2-х байт:
Ну а дальше вы догадались, для каждого варианта размера входного параметра n (кроме 8 бит) может существовать два варианта предподсчёта, в зависимости от того, которую из двух таблиц мы применяем. Думаю, читателю понятно, почему мы не можем просто так взять и завести таблицу BitsSetTableFFFFFFFF, однако вполне могут существовать задачи, где и это будет оправданным.
Быстро ли работает предподсчёт? Всё сильно зависит от размера, смотрите таблицы ниже. Первая для однобайтового предподсчёта, а вторая для двухбайтового.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 0,01 | 1,83 | 21,07 | 36,25 |
| x64 | 0,01 | 1,44 | 24,79 | 26,84 |
Интересный момент: для режима x64 предподсчёт для u64 работает заметно быстрее, возможно, это особенности оптимизации, хотя подобное не проявляется во втором случае.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | — | 0,05 | 7,95 | 13,01 |
| x64 | — | 0,07 | 8,49 | 13,01 |
Важное замечание: данный алгоритм с использованием предподсчёта оказывается выгодным только лишь при соблюдении следующих двух условий: (1) у вас есть лишняя память, (2) вам требуется выполнять расчёт числа единичных битов намного больше раз, чем размер самой таблицы, то есть имеется возможность «отыграть» время, потраченное на предварительное заполнение таблицы каким-то из нехитрых алгоритмов. Пожалуй, можно также иметь в виду экзотическое условие, которое на практике всегда выполнено. Вы должны гарантировать, что обращение к памяти само по себе быстрое и не замедляет работу других функций системы. Дело в том, что обращение к таблице может выбросить из кэша то, что там было изначально и замедлить таким образом какой-то другой участок кода. Косяк это вы вряд ли найдёте быстро, однако подобные чудовищные оптимизации едва ли кому-то понадобятся на практике при реализации обычных программ.
Умножение и остаток от деления
Возьмем же наконец более сильные зелья с нашей алхимической полки. С помощью умножения и остатка от деления на степень двойки без единицы можно делать довольно интересные вещи. Начнём творить заклинание с одного байта. Для удобства обозначим все биты одного байта латинскими буквами от «a» до «h». Наше число n примет вид:
Теперь разобьём мысленно наши 24 бита на 8 блоков по 3 бита в каждом (см. нижеследующую картинку, первую строку таблички). Затем с помощью побитового «и» с маской 0x249249 (вторая строка таблички) обнулим в каждом блоке два старших бита.
Третья строка таблицы поясняет шестнадцатеричную запись маски. В последней строке показан результат, которого мы добивались: все биты исходного байта содержаться каждый в своём трёхбитовом блоке, но в ином порядке (порядок нам и не важен).
Теперь внимание: мы должны сложить эти 8 блоков – и получим сумму наших бит!
В случае когда n имеет размер 16 бит можно разбить его на две части по 8 бит. Например, так:
Дело в том, что нам необходимо, чтобы все биты исходного числа заняли правильные позиции в своих 4-битовых блоках (картинка выше), а коль скоро 8 и 4 не являются взаимно простыми числами, обычное копирование 8 битов 4 раза не даст правильного расположения нужных битов. Нам придётся добавить к нашему байту один нолик, то есть тиражировать 9 битов, так как 9 взаимно просто с 4. Так мы получим число, имеющее размер 36 бит, но в котором все биты исходного байта стоят на младших позициях 4-битовых блоков. Осталось только взять побитовое «и» с числом 0x111111111 (вторая строка на картинке выше), чтобы обнулить по три старших бита в каждом блоке. Затем блоки нужно сложить.
При таком подходе программа подсчёта единичных битов в байте будет предельно простой:
Недостаток программы очевиден: требуется выход в 64-битовую арифметику со всеми вытекающими отсюда последствиями. Можно заметить, что в действительности данная программа задействует только 33 бита из 64-х (старшие 3 бита обнуляются), и в принципе можно сообразить, как перенести данные вычисления в 32-х битовую арифметику, но рассказы о подобных оптимизациях не входят в тему этого руководства. Давайте пока просто изучать приёмы, а оптимизировать их вам придётся самим уже под конкретную задачу.
Ответим на вопрос о том, какого размера может быть переменная n, чтобы данный трюк правильно работал для неё. Коль скоро мы берём остаток от деления на 15, такая переменная не может иметь размер больше 14 бит, в противном случае придётся применить ветвление, как мы делали это раньше. Но для 14 бит приём работает, если добавить к 14-ти битам один нолик, чтобы все биты встали на свои позиции. Теперь я буду считать, что вы в целом усвоили суть приёма и сможете сами без труда подобрать множитель для тиражирования и маску для обнуления ненужных битов. Покажу сразу готовый результат.
Эта программа выше показывает, как мог бы выглядеть код, будь у вас переменная размером 14 бит без знака. Этот же код будет работать с переменной в 15 бит, но при условии, что максимум лишь 14 из них равные единице, либо если случай, когда n=0x7FFF мы разберём отдельно. Это всё нужно понимать для того, чтобы написать правильный код для переменной типа u16. Идея в том, чтобы сначала «откусить» младший бит, посчитать биты в оставшемся 15-ти битовом числе, а затем обратно прибавить «откушенный» бит.
Здесь точно также можно было вместо трех ветвлений взять 3 остатка от деления, но я выбрал ветвистый вариант, на моём процессоре он будет работать лучше.
Для n размером 64 бита мне не удалось придумать подходящего заклинания, в котором было бы не так много умножений и сложений. Получалось либо 6, либо 7, а это слишком много для такой задачи. Другой вариант — выход в 128-битовую арифметику, а это уже не пойми каким «откатом» для нас обернётся, неподготовленного мага может и к стенке отшвырнуть 🙂
Давайте лучше посмотрим на время работы.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 39,78 | 60,48 | 146,78 | — |
| x64 | 6,78 | 12,28 | 31,12 | — |
Очевидным выводом из этой таблицы будет то, что 64-х битовая арифметика плохо воспринимается в 32-х битовом режиме исполнения, хотя в целом-то алгоритм неплох. Если вспомнить скорость алгоритма предподсчёта в режиме x64 для однобайтовой таблицы для случая u32 (24,79 с), то получим, что данный алгоритм отстаёт всего лишь на 25%, а это повод к соревнованию, воплощённому в следующем разделе.
Замена взятия остатка на умножение и сдвиг
Недостаток операции взятия остатка всем очевиден. Это деление, а деление – это долго. Разумеется, современные компиляторы знают алхимию и умеют заменять деление на умножение со сдвигом, а чтобы получить остаток, нужно вычесть из делимого частное, умноженное на делитель. Тем не менее, это всё равно долго! Оказывается, что в древних свитках заклинателей кода сохранился один интересный способ оптимизации предыдущего алгоритма. Мы можем суммировать k-битовые блоки не взятием остатка от деления, а ещё одним умножением на маску, с помощью которой обнуляли лишние биты в блоках. Вот как это выглядит для n размером в 1 байт.
Для начала снова тиражируем байт трижды и удаляем по два старших бита у каждого 3-битового блока с помощью уже пройденной выше формулы 0x010101⋅n & 0x249249.
Каждый трёхбитовый блок я для удобства обозначил заглавной латинской буквой. Теперь умножаем полученный результат на ту же самую маску 0x249249. Маска содержит единичный бит в каждой 3-й позиции, поэтому такое умножение эквивалентно сложению числа самого с собой 8 раз, каждый раз со сдвигом на 3 бита:
Что мы видим? Биты с 21 по 23 и дают нам нужную сумму! При этом переполнения в каком-либо из блоков справа невозможно, так как там ни в одном блоке не будет числа, большего 7. Проблема лишь в том, что если наша сумма равна 8, мы получим 0, но это не страшно, ведь этот единственный случай можно рассмотреть отдельно.
По сути, мы взяли код из предыдущего раздела и заменили в нём взятие остатка от деления на 7 на умножение, сдвиг и побитовое «И» в конце. При этом вместо 3-х ветвлений осталось лишь одно.
Чтобы составить аналогичную программу для 16 бит, нам нужно взять код из предыдущего раздела, в котором показано как это делается с помощью взятия остатка от деления на 15 и заменить данную процедуру умножением. При этом нетрудно заметить то, какие условия можно убрать из кода.
Для 32-х бит мы делаем то же самое: берём код из предыдущего раздела и, порисовав немного на бумаге, соображаем, каким будет сдвиг, если заменить остаток на умножение.
Для 64-х бит я тоже не смог придумать чего-то такого, чтобы не заставляло бы мой процессор выполнять роль печки.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 12,66 | 42,37 | 99,90 | — |
| x64 | 3,54 | 4,51 | 18,35 | — |
Приятно удивили результаты для режима x64. Как и ожидалось, мы обогнали предподсчёт с однобайтовой таблицей для случая u32. Можно ли вообще обогнать предподсчёт? Хороший вопрос 🙂
Параллельное суммирование
Пожалуй, это самый распространённый трюк, который очень часто повторяют друг за другом не вполне опытные заклинатели, не понимая, как он точно работает.
Начнём с 1 байта. Байт состоит из 4-х полей по 2 бита, сначала просуммируем биты в этих полях, произнеся что-то вроде:
Вот пояснительная картинка к данной операции (по-прежнему, обозначаем биты одного байта первыми латинскими буквами):
Одно из побитовых «И» оставляет только младшие биты каждого двухбитового блока, второе оставляет старшие биты, но сдвигает их на позиции, соответствующие младшим битам. В результате суммирования получаем сумму смежных битов в каждом двухбитовом блоке (последняя строка на картинке выше).
Теперь сложим парами числа, находящиеся в двухбитовых полях, помещая результат в 2 четырёхбитовых поля:
Нижеследующая картинка поясняет результат. Привожу её теперь без лишних слов:
Наконец, сложим два числа в четырёхбитовых полях:
Действуя по аналогии, можно распространить приём на любое число бит, равное степени двойки. Число строк заклинания равно двоичному логарифму от числа бит. Уловив идею, взгляните вскользь на 4 функции, записанных ниже, чтобы убедиться в правильности своего понимания.
На этом параллельное суммирование не заканчивается. Развить идею позволяет то наблюдение, что в каждой строчке дважды используется одна и та же битовая маска, что как будто наводит на мысль «а нельзя ли как-нибудь только один раз выполнить побитовое «И»?». Можно, но не сразу. Вот что можно сделать, если взять в качестве примера код для u32 (смотрите комментарии).
В качестве упражнения я бы хотел предложить доказать самостоятельно то, почему нижеследующий код будет точным отображением предыдущего. Для первой строки я даю подсказку, но не смотрите в неё сразу:
Аналогичные варианты оптимизации возможны и для остальных типов данных.
Ниже приводятся две таблицы: одна для обычного параллельного суммирования, а вторая для оптимизированного.
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 7,52 | 14,10 | 21,12 | 62,70 |
| x64 | 8,06 | 11,89 | 21,30 | 22,59 |
| Режим | u8 | u16 | u32 | u64 |
|---|---|---|---|---|
| x86 | 7,18 | 11,89 | 18,86 | 65,00 |
| x64 | 8,09 | 10,27 | 19,20 | 19,20 |
В целом мы видим, что оптимизированный алгоритм работает хорошо, но проигрывает обычному в режиме x86 для u64.
Комбинированный метод
Мы видим, что наилучшие варианты подсчёта единичных битов – это параллельный метод (с оптимизацией) и метод тиражирования с умножением для подсчёта суммы блоков. Мы можем объединить оба метода, получая комбинированный алгоритм.
Первое, что нужно сделать — выполнить первые три строки параллельного алгоритма. Это даст нам точную сумму битов в каждом байте числа. Например, для u32 выполним следующее:
Теперь наше число n состоит из 4 байт, которые следует рассматривать как 4 числа, сумму которых мы ищем:
Мы можем найти сумму этих 4-х байт, если умножим число n на 0x01010101. Вы теперь хорошо понимаете, что означает такое умножение, для удобства определения позиции, в которой будет находиться ответ, привожу картинку:
Ответ находится в 3-байте (если считать их от 0). Таким образом, комбинированный приём для u32 будет выглядеть так:
Скорость работы этого метода вы можете посмотреть сразу в итоговой таблице.
Итоговое сравнение
Я предлагаю читателю самостоятельно сделать интересующие его выводы, изучив две нижеследующие таблицы. В них я обозначил название методов, программы к которым мы реализовали, а также пометил прямоугольной рамкой те подходы, которые я считаю наилучшими в каждом конкретном случае. Тех, кто думал, что предподсчёт всегда выигрывает, ожидает небольшой сюрприз для режима x64.
Итоговое сравнения для режима компиляции x86.
Итоговое сравнения для режима компиляции x64.
Замечание
Ни в коем случае не рассматривайте итоговую таблицу как доказательство в пользу того или иного подхода. Поверьте, что на вашем процессоре и с вашим компилятором некоторые числа в такой таблице будут совершенно иными. К сожалению, мы никогда не можем точно сказать, который из алгоритмов окажется лучше в том или ином случае. Под каждую задачу нужно затачивать конкретный метод, а универсального быстрого алгоритма, к сожалению, не существует.
Я изложил те идеи, о которых знаю сам, но это лишь идеи, конкретные реализации которых в разных комбинациях могут быть очень разными. Объединяя эти идеи разными способами, вы можете получать огромное количество разных алгоритмов подсчёта единичных битов, каждый из которых вполне может оказаться хорошим в каком-то своём случае.
Спасибо за внимание. До новых встреч!
UPD: Инструкция POPCNT из SSE4.2 не включена в список тестирования, потому что у меня нет процессора, который поддерживает SSE4.2.